 Теорема. Если пирамиду пересечь плоскостью, параллельной основанию, то:
Теорема. Если пирамиду пересечь плоскостью, параллельной основанию, то:
1) боковые ребра и высота делятся ею на отрезки, из которых можно составить ряд равных отношений;
2) в сечении получается многоугольник, подобный основанию;
3) площадь основания и сечения относятся как квадраты их расстояний от вершины.
Поверхность пирамиды.
Поверхностью пирамиды называется сумма площадей всех её граней. Различают полную ( ) и боковую (
) и боковую ( ) поверхности:
) поверхности:  .
.
Теорема. Боковая поверхность правильной пирамиды равна половине произведения периметра основания на апофему:  .
.
Объём пирамиды равен одной трети произведения площади её основания на высоту: 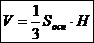 .
.
Усечённая пирамида
Усечённой пирамидой называется часть пирамиды, заключённая между плоскостью основания и плоскостью сечения, проведённого параллельно основанию.
Многоугольники ABCDE и A1B1C1D1E1 – нижнее и верхнее основания. Эти многоугольники подобны. Четырёхугольники AA1B1B, BB1C1C, CC1D1D, … - боковые грани, являются трапециями. Отрезки AA1, BB1, … – боковые рёбра. Перпендикуляр, опущенный из точки одного основания на плоскость другого, называется высотой.
 Усечённая пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усечённой пирамиды называется её апофемой. Боковые грани правильной усечённой пирамиды представляет собой равные равнобедренные трапеции.
Усечённая пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усечённой пирамиды называется её апофемой. Боковые грани правильной усечённой пирамиды представляет собой равные равнобедренные трапеции.
Поверхностью усечённой пирамиды называется сумма площадей всех её граней:
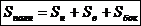 ,
,
где 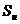 - площадь нижнего основания,
- площадь нижнего основания, 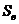 - площадь верхнего основания.
- площадь верхнего основания.
Теорема. Боковая поверхность правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему: 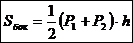 .
.
Объём усечённой пирамиды вычисляется по формуле:  .
.
Задачи.
1. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
2. В основании наклонной призмы лежит параллелограмм со сторонами 3 и 6 дм и острым углом 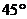 . Боковое ребро призмы равно 4 дм и наклонено к плоскости основания под углом
. Боковое ребро призмы равно 4 дм и наклонено к плоскости основания под углом 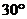 . Найдите объём призмы.
. Найдите объём призмы.
3. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
4. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
5. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
6. Основанием прямого параллелепипеда является ромб. Плоскость, проведённая через одну из сторон нижнего основания и противоположную сторону верхнего основания, образует с плоскостью основания угол 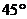 . Полученное сечение имеет площадь, равную Q. Определите боковую поверхность параллелепипеда.
. Полученное сечение имеет площадь, равную Q. Определите боковую поверхность параллелепипеда.
7. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
8. Диагональ прямоугольного параллелепипеда равна 13 см, а диагонали его боковых граней равны  и
и 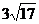 см. Определите объём параллелепипеда.
см. Определите объём параллелепипеда.
9. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
10. В основании пирамиды лежит прямоугольный треугольник с гипотенузой, равной c, и острым углом 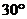 . Боковые рёбра пирамиды наклонены к плоскости основания под углом
. Боковые рёбра пирамиды наклонены к плоскости основания под углом 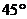 . Найдите объём пирамиды.
. Найдите объём пирамиды.
11. В основании пирамиды лежит равнобедренный треугольник с основанием 16 см и боковой стороной 10 см. Все боковые рёбра пирамиды наклонены к плоскости основания под углом α. Найдите объём пирамиды.
12. Основанием пирамиды является ромб с острым углом 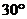 . Все боковые грани наклонены под углом
. Все боковые грани наклонены под углом 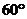 к плоскости основания. Определите объём и полную поверхность пирамиды, если радиус вписанного в ромб круга равен r.
к плоскости основания. Определите объём и полную поверхность пирамиды, если радиус вписанного в ромб круга равен r.
13. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
14. В правильной треугольной пирамиде боковое ребро длиной 12 см наклонено к плоскости основания под углом 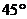 . Найдите радиус вписанной в основание пирамиды окружности.
. Найдите радиус вписанной в основание пирамиды окружности.
1) 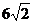 2)
2)  3)
3) 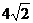 4)
4)  5)
5) 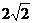
15. В правильной треугольной пирамиде боковое ребро длиной 14 см наклонено к плоскости основания под углом 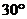 . Найдите длину стороны основания пирамиды.
. Найдите длину стороны основания пирамиды.
16. В правильной четырёхугольной пирамиде высота равна 4 см, апофема наклонена к плоскости основания под углом 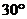 . Найдите радиус окружности, описанной около основания.
. Найдите радиус окружности, описанной около основания.
1) 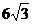 2)
2) 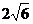 3)
3) 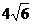 4)
4)  5)
5) 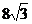
17. Плоский угол при вершине правильной треугольной пирамиды равен 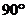 . Найдите отношение боковой поверхности пирамиды к площади её основания.
. Найдите отношение боковой поверхности пирамиды к площади её основания.
18. Найдите отношение объёма куба к объёму правильного тетраэдра, ребро которого равно диагонали грани куба.
19. Центр верхнего основания куба с ребром, равным a, соединён с серединами сторон нижнего основания, которые также соединены в последовательном порядке. Вычислите полную поверхность полученной пирамиды.
20. Определите объём правильной четырёхугольной усечённой пирамиды, если её диагональ равна 18 см, а длины сторон оснований 14 и 10 см.
21. Основаниями правильной усечённой пирамиды являются квадраты со сторонами a и b (a > b). Боковые рёбра наклонены к плоскости основания под углом 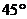 . Определите объём усечённой пирамиды.
. Определите объём усечённой пирамиды.