Решение: Пусть имеется некоторый план работ, который моделируется сетевым графиком – взвешенным ориентированным графом 
, у которого V – множество вершин графа, E – множество дуг графа: 
. Дуги соответствуют работам проекта, вершины графа – событиям, обозначающим начало и/или конец этапов. Каждая дуга нагружена числом – временем, необходимым на выполнение этой операции. Нагрузку на дуге (время) обозначим 
.
Сетевой график должен удовлетворять следующим условиям:
1) Во множестве вершин V имеются две вершины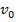 
и 
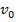, такие, что из вершины дуги только выходя, а в вершину дуги только входят. Вершина 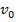называется начальной, а вершина – конечной вершиной сетевого графика. Начальная вершина соответствует моменту начала проекта, а конечная вершина – моменту завершения проекта.
2) Для всякой промежуточной вершины 
, т.е. не являющейся ни начальной, ни конечной, существуют два пути в сетевом графике от начальной вершины до рассматриваемой 
и от рассматриваемой вершины до конечной 
.
3) В сетевом графике нет циклов.
При анализе сетевого графика ставятся следующие задачи:
1) Отыскание минимального времени выполнения всего проекта (критического времени).
2) Отыскание тех операций, которые существенно влияют на критическое время; их совокупность образует так называемый критический путь.
3) Отыскание резервов времени.
Сетевой график определяется заданием:
- всех видов работ по проекту;
- времени, необходимого на выполнение каждой операции (работы) проекта;
- последовательностью выполнения работ (для каждой работы указываются работы, предшествующие ее выполнению).
Событие не может наступить, пока не будут выполнены все предшествующие этому событию работы. Поэтому рассчитывают ранний (ожидаемый) срок наступления события 
.
Ранним временем наступления события называется длина максимального пути 
от начала всех работ 
до момента . Длина пути 
определяется как сумма длин всех его дуг. Обозначим раннее время
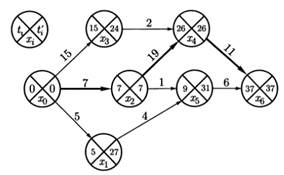
Рис.1. Пример сетевого графика
Графически будем изображать сетевой график, как показано на рис. 1. Кружки, изображающие события – вершины графа – разделим на части: в нижней записываем обозначение события , в левой записываем 
– раннее время наступления события , а в правой записываем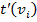 
– позднее время наступления события .
По определению 
. Раннее время момента завершения всех работ 
называется критическим временем сетевого графика, а путь 
, длина которого равна критическому времени, называется критическим путем сетевого графика.
Критический путь обладает наибольшей продолжительностью, он определяет минимум временных затрат необходимых на выполнение проекта.
Работы, составляющие критический путь, называются критическими работами.
Расчет ранних времен наступлений событий можно вести по формуле прямой волны:
В этой формуле рассматриваются для всех соседних к предшествующих вершин 
наибольшая из сумм раннего времени вершины-соседки и длительности работы от нее до заданной вершины.
Рассчитаем раннее время для отдельных событий на рис.1. Ранее отмечалось, что 
.
Найдем 
, 
, 
:
Рассчитав ранее время всех событий, определяется критическое время и соответствующий критический путь.
В примере: критическое время 
, критический путь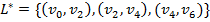 
.
Поздним временем наступления события называется разность критического времени 
сетевого графика и длины максимального пути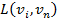 
от момента до окончания всех работ. Обозначим позднее время:
По определению имеем для конечной вершины:
Позднее время удобно считать по формуле обратной волны:
начиная от конечной вершины к начальной. В этой формуле рассматриваются все соседние к последующие вершины 
.
Позднее время наступления события – самое позднее время завершения работы, гарантирующее завершение всего проекта без задержки.
Рассчитаем позднее время для отдельных событий на рис.1. Ранее отмечалось, что 
.
Найдем 
, 
, 
, 
:
Рассмотрим резервы времени.
Резерв времени 
события определяется как разность между поздним и ранним сроками его наступления:
Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличение срока выполнения всего проекта. Критические события резервов не имеют, т.к. любая задержка в наступлении события, лежащего на критическом пути, вызовет такую же задержку в наступлении конечного события.
Полным резервом времени 
для работы 
называется величина:
Полный резерв времени работы показывает, насколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. Важным свойством полного резерва времени работы является то, что он принадлежит не только этой работе, но и всем максимальным путям, проходящим через нее. При использовании полного резерва времени только для одной работы резервы времени остальных работ, лежащих на максимальном пути, проходящим через нее, будут полностью исчерпаны.
Свободным резервом времени 
для работы называется величина:
Свободный резерв времени работы представляет собой часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего времени наступления ее конечного события.
Так, например:
Анализ резервов времени позволяет сделать вывод о том, что все работы вне критического пути могут быть сделаны за более длительный срок, т.е. меньшими бригадами, без простоев, а значит дешевле.
Тема 5