[2]: гл.7, §§ 1-3,
Вопросы для самопроверки
- Что такое конечный автомат?
- Какие виды автоматов существуют?
- Какие существуют способы задания автоматов?
- Чем детерминированный автомат отличается от недетерминированного?
- Что означает эквивалентность автоматов?
- Что такое автомат Мили?
- Что такое автомат Мура?
- Алгоритм минимизации конечного автомата?
Задача 1
Опишем работу кодового замка с пятью кнопками. Назовем их А, В,С, Д, Е. Замок открывается при нажатии одной кнопки (В), остается открытым 5 сек., причем никакие две кнопки одновременно не набираются.
Решение: Множество входных символов содержит 6 символов: Х={ А, В,С, Д, Е, *}, множествоУ выходных символов содержит символ0 – замок закрыт, 1 – замок открыт. Так как замок открывается при нажатии только одной кнопки, то выходной сигнал зависит только от одного входного символа. Таким образом, любое кодовое слово, имеющее В вконце открывает замок, например, Д*С*А*В. У такого замка может быть только два состояния q0 – он закрыт и не реагирует ни на какие нажатия, кроме В, и состояние, когда он среагировал на В и из q0перешел в q1, а дверь открылась.Любое нажатие влечет за собой закрытие двери и переход автомата обратно вq0. Учитывая, что две клавиши одновременно не набираются, клавишу В рано или поздно придется отпустить, тогда будет подаваться *, и дверь закроется.
Такой кодовый замок задается таблицей.
| А | В | С | Д | Е | * | |
| q0 | q0|0 | q1|1 | q0|0 | q0|0 | q0|0 | q0|0 |
| q1 | q0|0 | q1|1 | q0|0 | q0|0 | q0|0 | q0|0 |
Тема 6
Элементы теории кодирования
[2]: гл.6, §§ 1-5,
Вопросы для самопроверки
- Что такое кодирование?
- Какие бывают виды кодов?
- Что значит взаимно-однозначное кодирование?
- В чем суть кода Фано?
- В чем суть кода Хаффмана?
- В чем суть кода Хэмминга?
Задача 1
Закодировать по Фано сообщения, имеющие следующие вероятности:
| символ | |||||||
| вероятность | 0,4 | 0,2 | 0,1 | 0,1 | 0,1 | 0,05 | 0,05 |
Проверим выполнимость необходимого условия:
0,4 + 0,2 + 0,1 + 0,1 + 0,1+ 0,1 + 0,05 + 0,05 = 1.
Составим соответствующую таблицу:

Найдем стоимость кода (средняя длина кодового слова). Он является критерием степени оптимальности кодирования. Вычислим ее в нашем случае.
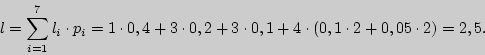
Задача 2
Закодировать по Хаффману сообщения, имеющие следующие вероятности:
| символ | |||||||
| вероятность | 0,4 | 0,2 | 0,1 | 0,1 | 0,1 | 0,05 | 0,05 |
Решение.

Вторым шагом производим кодирование, "проходя" по таблице справа налево (обычно это проделывается в одной таблице):

Найдем стоимость кода (средняя длина кодового слова). Он является критерием степени оптимальности кодирования.

Задача 3
Для заданного сообщения Х = 0110101 построить код Хэмминга Х/, внести одиночную ошибку и произвести декодирование.
Решение: Обозначим информационные символы через α3 = 0, α5 = 1, α6 = 1, α7 = 0, α9=1, α10 = 0, α11 = 1.
Вычислим контрольные символы:
α1 = α3 + α5 + α7 + α9 + α11 = 0 + 1 + 0 + 1 + 1 = 1
α2 = α3 + α6 + α7 + α10 + α11 = 0 + 1 + 0 + 0 + 1 = 0
α4 = α5 + α6 + α7 = 1 + 1 + 0 = 0
α8 = α9 + α10 + α11 = 1 + 0 + 1 = 0.
Получим код Х/ = 10001100101.
Пусть при передаче сообщения Х/произошла ошибка замещения в 7 – м разряде, т.е. получено сообщение Х// = 10001110101. Докажем это, для этого вычислим
β1 = α1/ + α3 /+ α5 /+ α7/+ α9 /+ α11/ = 1 + 0 + 1 + 1 + 1 + 1 = 1
β2 = α2/ + α3/+ α6 /+ α7/+ α10 /+ α11/ = 0 +0 + 1 + 1 + 0 +1 = 1
β3 = α4/+ α5 /+ α6 /+ α7/ = 0 + 1 + 1 + 1 = 1
β4 = α8/+ α9 /+ α10 /+ α11/ = 0 + 1 + 0 + 1 = 0.
Разряд, в котором произошла ошибка, равен S = 01112 = 7.
Задачи контрольной работы
Задачи 01-20
1. Сколько четырехзначных чисел можно записать с помощью цифр 0, 1, 2, 3, 4, 5, если
a) каждая цифра входит в число только один раз?
b) цифры в числе могут повторяться?
c) это число делится нацело на 4?
d) сколько существует множеств, содержащих 4 любых цифры из указанных?
e) числа не начинаются с 35?
2. Сколько пятизначных чисел можно записать с помощью цифр 0, 1, 2, 3, 4, 5, 6, если
a) каждая цифра входит в число только один раз?
b) цифры в числе могут повторяться?
c) это число делится нацело на 5?
d) в скольких из них каждая следующая цифра больше предыдущей?
e) числа не начинаются с 35?
3. Сколько четырехзначных чисел можно записать с помощью цифр 0, 1, 2, 3, 4, 5, 6, если
a) каждая цифра входит в число только один раз?
b) цифры в числе могут повторяться?
c) это число делится нацело на 4?
d) сколько существует множеств, содержащих 4 любых цифры из указанных?
e) в скольких из них каждая следующая цифра меньше предыдущей?
4. Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5-ти различных цветов (красный, синий, желтый, зеленый, белый) так, чтобы
a) все полосы имели различные цвета?
b) одна из полос должна быть красной?
c) ни одна из полос не должна быть красной?
d) полосы могут иметь одинаковый цвет?
5. Существуют матрицы размерности (3,4), состоящие из 0 и 1, они называются бинарными.
a) сколько существует матриц размерности (3,4), состоящих из 0 и 1?
b) сколько среди таких матриц, у которых различны все строки?
c) сколько среди таких матриц, у которых различны все столбцы?
d) сколько среди таких матриц, у которых различны все строки и столбцы?
6. Сколько существует шестизначных телефонных номеров,
a) состоящих из различных цифр?
b) могут содержать одинаковые цифры?
c) которые являются четными?
d) которые начинаются с числа 44?
7. Имеется 10 электронных документов.
a) сколькими способами три из них можно поместить в очередь на печать на лазерном принтере?
b) электронные документы передаются по семи каналам связи из пункта А в пункт В. В пункте В документы редактируются и передаются обратно в пункт А. Сколькими способами можно передать документы из пункта А в пункт В и обратно?
c) сколькими способами их можно передать по электронной почте, если каждый документ передается отдельно?
d) сколькими способами их можно передать по электронной почте, если документы А и В должны быть переданы вместе?
8. Имеется 10 символов, которые можно использовать для составления пятибуквенного кода электронного документа?
a) сколько существует таких кодов?
b) сколько кодов не имеют повторяющихся символов?
c) сколько кодов содержат два указанных символа α и β?
d) сколько кодов начинаются с символа α или β?
9. Сколькими способами можно расположить в 12 лузах 3 белых шара и 9 черных
a) часть луз может быть пустой и лузы считаются различными?
b) ни одна из луз не может быть пустой?
c) в первой лузе должен лежать белый шар и нет пустых луз?
d) все шары считаются различными?
10. Двенадцать человек, включая Мари и Петера, являются кандидатами в комитет пяти.
a) сколько разных комитетов можно набрать из 12 человек?
b) сколько из них включают либо Мари, либо Петера, но не обоих?
c) сколько из них включают Мари и Петера?
d) сколько из них включают Мари или Петера?
11. Под словом из букв слова «АБРАКАДАБРА» понимают любую последовательность всех букв этого слова.
a) сколько разных слов можно получить из букв слова «АБРАКАДАБРА»?
b) сколько разных слов, начинающихся с буквы «К» можно получить из слова «АБРАКАДАБРА»?
c) сколько разных слов можно получить из букв слова «АБРАКАДАБРА», в которых никакие две буквы А не стоят рядом?
d) сколько разных слов, оканчивающихся на «ДА», можно получить из букв слова «АБРАКАДАБРА?
12. Автобусные билеты имеют шестизначные номера от 000000 до 999999.
a) сколько номеров, у которых есть хотя бы одна нечетная цифра?
b) сколько номеров содержат цифру 7?
c) сколько номеров содержат цифру 7 и 0?
d) сколько среди них счастливых? (Счастливым считается номер abcabc или abccba).
13. Забор состоит из 10 досок. У маляра Васи есть краска 4 разных цветов.
а) сколькими способами маляр Вася может покрасить забор?
b) сколькими способами он может покрасить лишь одну доску забора?
c) в бригаде маляров кроме Васи есть еще маляры Люся и Нюся. Сколькими способами кто-то из них может покрасить лишь одну доску забора?
d) Вася, Люся и Нюся работают с понедельника по пятницу. Сколькими способами кто-то из них может покрасить лишь одну доску забора в рабочий день?
14. В алфавите племени Мумба – Юмба 5 букв: М, У, Б, А, Ю. Словом в словаре этого племени является последовательность не более чем 4 букв.
a) сколько всего слов в словаре этого племени?
b) сколько слов имеют хотя бы одну гласную букву?
c) сколько слов состоят только из согласных букв?
d) сколько слов начинаются с буквы М?
15. а) Сколько существует четырехзначных чисел?
b) сколько четырехзначных чисел, не превосходящих 6000, можно составить, используя только нечетные цифры?
c) сколько существует четных четырехзначных чисел без повторения цифр?
d) сколько существует четных четырехзначных чисел, в которых цифры могут повторяться?
16. В один из комитетов парламента нужно отобрать трех членов, причем выбирать надо из 5 консерваторов, 3 лейбористов и 4 либерал-демократов.
a) сколько разных комитетов можно составить?
b) сколько разных комитетов можно составить, если в него должен входить по крайней мере один либерал-демократ?
c) сколько разных комитетов можно составить, если в него должен входить только один либерал-демократ?
d) сколько разных комитетов можно составить, если в него не должен входить ни один либерал-демократ?
17. Компания, состоящая из 10 супружеских пар, разбивается на 5 групп по 4 человека для лодочной прогулки.
a) сколькими способами это можно сделать?
b) во скольких случаях данные двое мужчин окажутся в одной лодке со своими женами?
c) во скольких случаях никакие мужчины не окажутся в одной лодке со своими женами?
d) во скольких случаях в каждой лодке окажутся двое мужчин и две женщины?
18. В небольшой фирме восемь человек работают на производстве, пятеро – в отделе сбыта, и трое – в бухгалтерии. Для обсуждения новой продукции было решено пригласить на совещание шестерых работающих.
a) сколькими способами это можно сделать?
b) сколькими способами это можно сделать,если необходимы представители каждого из трех отделов?
c) сколькими способами это можно сделать,если необходимо пригласить хотя бы двух представителей отдела сбыта?
d) сколькими способами это можно сделать,если необходимо участие всех представителей бухгалтерии?
19. Под словом из букв слова «ЛОГАРИФМ» понимают любую последовательность всех букв этого слова.
a) сколько разных слов можно получить из букв слова «ЛОГАРИФМ»?
b) сколько разных слов, начинающихся с буквы «Л» можно получить из букв слова «ЛОГАРИФМ»?
c) сколько разных слов можно получить из букв слова «ЛОГАРИФМ», в которых буквы А и И не стоят рядом?
d) Сколькими разными способами можно переставить буквы слова «ЛОГАРИФМ» так, чтобы второе, четвертое и шестое места были заняты согласными буквами?
20. Под словом из букв слова «ПАСТУХ» понимают любую последовательность всех букв этого слова.
a) Сколькими разными способами можно переставить буквы слова «пастух» так, чтобы между двумя гласными были две согласные буквы?
b) сколько разных слов можно получить из букв слова «ПАСТУХ»?
c) сколько разных слов, начинающихся с буквы «П» можно получить из букв слова «ПАСТУХ»?
d) сколько разных слов можно получить из букв слова «ПАСТУХ», в которых буквы А и У не стоят рядом?
Задачи 21-40
Найти решение следующих выражений:
21. а)  б)
б)  ; в)
; в) 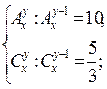
г) Найти коэффициент при x3 в выражении (1+x)3+(1+x)4+  +(1+x)15.
+(1+x)15.
22. а)  б)
б) 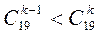 ; в)
; в) 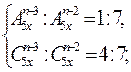
г) В разложении 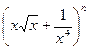 биномиальный коэффициент третьего члена на 44 больше коэффициента второго члена. Найти член, не содержащий x.
биномиальный коэффициент третьего члена на 44 больше коэффициента второго члена. Найти член, не содержащий x.
23. а)  ; б)
; б)  ; в)
; в) 
г)Определить коэффициент k в ka6b6c12следующем члене многочлена получаемого из алгебраического выражения (a+b+c)3(a2+b2+c2)6:
24. а)  б)
б)  ; в)
; в) 
г)Определить коэффициент k в ka2b6c6следующем члене многочлена получаемого из алгебраического выражения (a+b+c)3(a2+b2+c2)6:
25. а)  ; б)
; б) 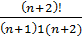 <1000; в)
<1000; в) 
г)Найти x, если второй член разложения 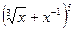 равен 20;
равен 20;
26. а)  ; б)
; б) 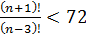 в)
в) 
г)Найти x, если четвертый член разложения  равен
равен 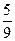 .
.
27. а)  ; б)
; б)  в)
в) 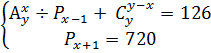
г)Найти x, если четвертый член разложения  равен
равен 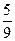 .
.
28.а)  ; б)
; б) 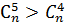 в)
в) 
г)Найти четвертый член разложения бинома  , если отношение коэффициента второго члена к коэффициенту первого члена равно
, если отношение коэффициента второго члена к коэффициенту первого члена равно  .
.
29. а)  ; б)
; б)  в)
в) 
г) Найдите коэффициент при  а
а  с после раскрытия скобок в выражении (а+ в + с + 5)10.
с после раскрытия скобок в выражении (а+ в + с + 5)10.
30. а)  ; б)
; б) 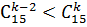 в)
в) 
г) Найдите коэффициент при  а
а  с после раскрытия скобок в выражении (а+ в – с + 5)11.
с после раскрытия скобок в выражении (а+ в – с + 5)11.
31. а)  ; б)
; б) 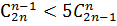 в)
в) 
г) Найдите коэффициент при  а
а  с после раскрытия скобок в выражении (а – в– с + 5)11.
с после раскрытия скобок в выражении (а – в– с + 5)11.
32. а)  ; б)
; б) 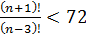 ; в)
; в) 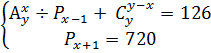
г)Найти x, если второй член разложения  равен 20;
равен 20;
33. а)  ; б)
; б)  в)
в) 
г)Найти x, если четвертый член разложения 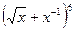 равен
равен 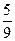 .
.
34. а)  ; б)
; б) 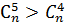 в)
в) 
г)Найти x, если четвертый член разложения 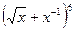 равен
равен 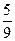 .
.
35.а)  ; б)
; б)  в)
в) 
г)Найти четвертый член разложения бинома  , если отношение коэффициента второго члена к коэффициенту первого члена равно
, если отношение коэффициента второго члена к коэффициенту первого члена равно  .
.
36. а)  ; б)
; б) 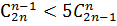 в)
в) 
г) Найдите коэффициент при  а
а  с после раскрытия скобок в выражении (а+ в + с + 5)10.
с после раскрытия скобок в выражении (а+ в + с + 5)10.
37. а)  ; б)
; б) 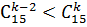 в)
в) 
г) Найдите коэффициент при  а
а  с после раскрытия скобок в выражении (а – в– с + 5)11.
с после раскрытия скобок в выражении (а – в– с + 5)11.
38.а) 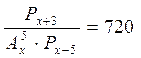 ; б)
; б) 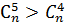 в)
в) 
г)Найти четвертый член разложения бинома 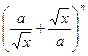 , если отношение коэффициента второго члена к коэффициенту первого члена равно
, если отношение коэффициента второго члена к коэффициенту первого члена равно  .
.
39. а)  ; б)
; б)  в)
в) 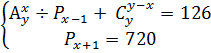
г)Найти x, если четвертый член разложения 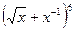 равен
равен 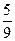 .
.
40. а) 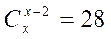 ; б)
; б)  в)
в) 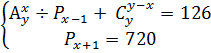
г)Найти x, если четвертый член разложения  равен
равен 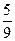 .
.
Задачи 41-60
Задайте данный неориентированный граф матрицей смежности, матрицей инцидентностей, списком дуг и структурой смежности. Определите его остов, радиус, диаметр и центр, хроматическое и цикломатическое число.
41. V= 
42. V= 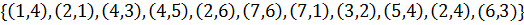
43. V= 
44.V= 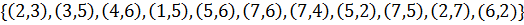
45. V= 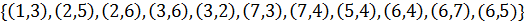
46. V= 
47.V= 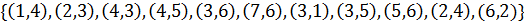
48. V= 
49. V= 
50. V= 
51.V= 
52. V= 
53. V= 
54.V= 
55. V= 
56. V= 
57.V= 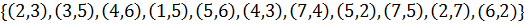
58. V= 
59. V= 
60.V= 
Задачи 61-80
61 а)Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время | ||||||||||||||||
| Предшественники | - | - | - | A1 | A4 | A2 A5 | A6 | A3 A7 | A4 | A4 | A6 | A6 | A10 A12 | A6 | A9 A11 | A14 A8 |
б)Рассматривая это граф, как транспортную сеть, построит максимальный поток сети.
в)Рассматривая граф, как ориентированный взвешенный граф, выбрать произвольные две вершины, кроме u0 и v0 , и найти путь кратчайшей длины между этими вершинами.
62. а) Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время | ||||||||||||||||
| Предшественники | - | - | - | A1 | A4 | A2 A5 | A6 | A3 A7 | A4 | A4 | A6 | A6 | A10 A12 | A6 | A9 A11 | A14 A8 |
б)Рассматривая это граф, как транспортную сеть, построить максимальный поток сети.
в)Рассматривая граф, как ориентированный взвешенный граф, выбрать произвольные две вершины, кроме u0 и v0 , и найти путь кратчайшей длины между этими вершинами.
63. а) Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время | ||||||||||||||||
| Предшественники | - | - | - | A1 | A4 | A2 A5 | A6 | A3 A7 | A4 | A4 | A6 | A6 | A10 A12 | A6 | A9 A11 | A14 A8 |
б)Рассматривая это граф, как транспортную сеть, построит максимальный поток сети.
в)Рассматривая граф, как ориентированный взвешенный граф, выбрать произвольные две вершины, кроме u0 и v0 , и найти путь кратчайшей длины между этими вершинами.
64. Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время | ||||||||||||||||
| Предшественники | - | - | - | A1 | A4 | A2 A5 | A6 | A3 A7 | A4 | A4 | A6 | A6 | A10 A12 | A6 | A9 A11 | A14 A8 |
б)Рассматривая это граф, как транспортную сеть, построит максимальный поток сети.
в)Рассматривая граф, как ориентированный взвешенный граф, выбрать произвольные две вершины, кроме u0 и v0 , и найти путь кратчайшей длины между этими вершинами.
65. Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время | ||||||||||||||||
| Предшественники | - | - | - | A1 | A4 | A2 A5 | A6 | A3 A7 | A4 | A4 | A6 | A6 | A10 A12 | A6 | A9 A11 | A14 A8 |
б)Рассматривая это граф, как транспортную сеть, построит максимальный поток сети.
в)Рассматривая граф, как ориентированный взвешенный граф, выбрать произвольные две вершины, кроме u0 и v0 , и найти путь кратчайшей длины между этими вершинами.
66. Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время | ||||||||||||||||
| Предшественники | - | - | - | A1 | A4 | A2 A5 | A6 | A3 A7 | A4 | A4 | A6 | A6 | A10 A12 | A6 | A9 A11 | A14 A8 |
б)Рассматривая это граф, как транспортную сеть, построит максимальный поток сети.
в)Рассматривая граф, как ориентированный взвешенный граф, выбрать произвольные две вершины, кроме u0 и v0 , и найти путь кратчайшей длины между этими вершинами.
67. а) Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время | ||||||||||||||||
| Предшественники | - | - | - | A1 | A4 | A2 A5 | A6 | A3 A7 | A4 | A4 | A6 | A6 | A10 A12 | A6 | A9 A11 | A14 A8 |
б)Рассматривая это граф, как транспортную сеть, построит максимальный поток сети.
в)Рассматривая граф, как ориентированный взвешенный граф, выбрать произвольные две вершины, кроме u0 и v0 , и найти путь кратчайшей длины между этими вершинами.
68. Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время | ||||||||||||||||
| Предшественники | - | - | - | A1 | A4 | A2 A5 | A6 | A3 A7 | A4 | A4 | A6 | A6 | A10 A12 | A6 | A9 A11 | A14 A8 |
б)Рассматривая это граф, как транспортную сеть, построит максимальный поток сети.
в)Рассматривая граф, как ориентированный взвешенный граф, выбрать произвольные две вершины, кроме u0 и v0 , и найти путь кратчайшей длины между этими вершинами.
69. Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время | ||||||||||||||||
| Предшественники | - | - | - | A1 | A4 | A2 A5 | A6 | A3 A7 | A4 | A4 | A6 | A6 | A10 A12 | A6 | A9 A11 | A14 A8 |
б)Рассматривая это граф, как транспортную сеть, построит максимальный поток сети.
в)Рассматривая граф, как ориентированный взвешенный граф, выбрать произвольные две вершины, кроме u0 и v0 , и найти путь кратчайшей длины между этими вершинами.
70. Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время | ||||||||||||||||
| Предшественники | - | - | - | A1 | A4 | A2 A5 | A6 | A3 A7 | A4 | A4 | A6 | A6 | A10 A12 | A6 | A9 A11 | A14 A8 |
б)Рассматривая это граф, как транспортную сеть, построит максимальный поток сети.
в)Рассматривая граф, как ориентированный взвешенный граф, выбрать произвольные две вершины, кроме u0 и v0 , и найти путь кратчайшей длины между этими вершинами.
71. а)Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время | ||||||||||||||||
| Предшественники | - | - | - | A1 | A4 | A2 A5 | A6 | A3 A7 | A4 | A4 | A6 | A6 | A10 A12 | A6 | A9 A11 | A14 A8 |
б)Рассматривая это граф, как транспортную сеть, построит максимальный поток сети.
в)Рассматривая граф, как ориентированный взвешенный граф, выбрать произвольные две вершины, кроме u0 и v0 , и найти путь кратчайшей длины между этими вершинами.
72. а) Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время | ||||||||||||||||
| Предшественники | - | - | - | A1 | A4 | A2 A5 | A6 | A3 A7 | A4 | A4 | A6 | A6 | A10 A12 | A6 | A9 A11 | A14 A8 |
б)Рассматривая это граф, как транспортную сеть, построит максимальный поток сети.
в)Рассматривая граф, как ориентированный взвешенный граф, выбрать произвольные две вершины, кроме u0 и v0 , и найти путь кратчайшей длины между этими вершинами.
73. а) Найти критический путь и минимальное время выполнения работы для графа, заданного сетью планирования.
| Вид работы | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| Время |
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2018-12-21 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд