Сборник
Вопросов и задач для самостоятельной подготовки к защите
лабораторных работ по физике
Раздел 1 «Механика»
(для студентов всех специальностей)
Настоящий сборник является первой частью «Сборника вопросов и задач для самостоятельной подготовки к защите лабораторных работ по общей физике» и содержит билеты к лабораторным работам №1, №2, №5, №10. В каждом билете содержится один теоретический вопрос и одна задача.
Нумерация работ соответствует принятой на кафедре физики МГУПП.
ЛАБОРАТОРНАЯ РАБОТА 1
ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТЕЛ ПРАВИЛЬНОЙ
ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
Билет 1.
1. Расскажите о штангенциркуле и о проведении измерений с помощью этого прибора.
2. Вычислить объем шара, если его радиус R= (15,73 + 0,02) мм.
Билет 2.
1. Расскажите о микрометре и о проведении измерений с помощью этого прибора.
2. Вычислить предельную абсолютную погрешность измерения плотности куба, если его ребро a = (10,12 + 0,08) мм, а масса m = (7,3 + 0,1) г.
Билет 3.
1. Каким образом определяется погрешность прямых измерений? В каком виде записывается окончательный результат измерения, и каков физический смысл такой записи?
2. Найти площадь квадрата, если его сторона a = (24,2 + 0,3) мм. Чему равна относительная погрешность измерения площади квадрата?
Билет 4.
1. Что называется ценой деления, точностью прибора? Как можно определить эти величины? Чему равна приборная погрешность инструментов, которыми Вы пользовались?
2. Вычислить предельную абсолютную погрешность измерения плотности цилиндра, если его объем V = (105 + 1) ×102 мм3 , а масса m = (85,2 + 0,6) г.
Билет 5.
1. Какие погрешности называют систематическими, случайными? Как они возникают?
2. Найти плотность материала куба, если его масса m = (1,50 + 0,02) г, высота ребра h = (5,91 + 0,01) мм.
Билет 6.
1. Какие измерения называются прямыми? Как определяется предельная погрешность этих измерений? Как правильно записывается результат этих измерений? Приведите примеры.
2. Определить относительную погрешность измерения площади шара, если его радиус R = (8,80 + 0,02) см.
Билет 7.
1. Какие измерения называются косвенными? Как определяется абсолютная и относительная погрешности этих измерений?
2. Найти площадь боковой поверхности цилиндра, если радиус его основания R = (38,4 + 0,8) мм, а высота h = (80,1 + 0,9) мм.
Билет 8.
1. Какая величина называется предельной относительной погрешностью результата измерения? С какой целью вводится эта величина? Какие численные значения e допустимы в лабораторных измерениях?
2. Определить предельную относительную погрешность измерения объема куба, если его ребро 15,3 см, приборная погрешность 0,05 см, а средняя абсолютная погрешность 0,03 см.
Билет 9.
1. Как проводятся измерения приборами, снабженными нониусом? Какова была приборная погрешность штангенциркуля, которым Вы пользовались при выполнении этой лабораторной работы?
2. Найти объем конуса, если радиус основания R = (15,22 + 0,04) см, а высота h = (48,1 + 0,8) см.
Билет 10.
1. Как определяется объем кольца? Как вычислялись относительная и абсолютная погрешности объема кольца?
2. Найти объем параллелепипеда, если его основанием является квадрат со стороной a = (22,4 + 0,6) мм, а его высота h = (88,8 + 0,8) мм.
Билет 11.
1. Какая величина называется плотностью вещества? В каких единицах она измеряется в системе СИ?
2. Найти объем цилиндра, если радиус основания R = (58,4 + 0,5) мм, а высота его равна h = (122,8 + 0,2) мм.
Билет 12.
1. Как определяется предельная абсолютная погрешность прямых измерений? Приведите примеры из лабораторной работы 1.
2.Найти плотность материала пирамиды, если ее объем
V = (118 + 2)×102 мм3, а ее масса m = (93,4 + 0,7) г.
Билет 13.
1. Какие погрешности называют систематическими, случайными? Какова природа возникновения этих ошибок, и как они учитываются в лабораторной работе 1?
2. Найти площадь ромба, если его сторона a = (31,4 + 0,9) мм, а высота h = (56,4 + 0,2) мм.
Билет 14.
1. Какие измерения называются косвенными? Как определяются абсолютная и относительная погрешности этих измерений? Приведите примеры таких измерений из лабораторной работы 1.
2. Найти площадь параллелепипеда, если его основанием является прямоугольник со сторонами a = (14,3 + 0,5) мм и b = (18,6 + 0,8) мм, а его высота h = (34,6 + 0,1) мм.
Билет 15.
1. Как определяются предельная абсолютная и относительная погрешности прямых измерений? Приведите примеры из лабораторной работы 1.
2. Вычислить площадь боковой поверхности куба, если его ребро h = (39,2 + 0,8) мм.
ЛАБОРАТОРНАЯ РАБОТА 2
ИССЛЕДОВАНИЕ ЗАКОНОВ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ И ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ
Билет 1.
1.Как в работе проверялась формула скорости равноускоренного движения?
2. Тело массой 200 г падает вертикально вниз с ускорением 920 см/с2. Чему равна сила сопротивления воздуха?
Ответ: 0,12 Н
Билет 2.
1. Как в работе проверялось соотношение V1:V2:V3 = t1:t2:t3? Откуда оно следует?
2. Чему равен вес человека, который равноускоренно начал подниматься в лифте с ускорением 1 м/с2. Масса человека 70 кг.
Ответ: 756 Н.
Билет 3.
1. Как в работе осуществлялась проверка основного закона динамики материальной точки?
2. Найти ускорение, с которым будут двигаться грузы с
массами m и 3m. Массами блока и нитей пренебречь,
трение не учитывать.
Ответ: 4,9 м/с2.
 |  | ||
m 3m
Билет 4.
1. Как в работе осуществлялась проверка формулы пути равноускоренного движения?
2. Тело скользит равномерно по наклонной плоскости с углом наклона45°. Определить коэффициент трения тела о плоскость.
Ответ: 1.
Билет 5.
1. Как в работе проверялось соотношение F1t1:F2t2:F3t3 = V1:V2:V3? Откуда оно следует?
2. Тело брошено горизонтально с некоторой высоты со скоростью 20 м/с. Какова его скорость через 2 с?
Ответ: 28 м/с.
Билет 6.
1. Напишите уравнение движения и формулу скорости для равно-
переменного движения. Какая величина называется мгновенной скоростью и ускорением? Как определяется средняя скорость движения?
2. Массы грузов соответственно равны m1 = 1,5 кг,
m2 = 0,5 кг. Груз 2 удерживался электромагнитом.
После его отключения система пришла в движение.
Найти ускорение грузов. Трением в блоке и массой блока пренебречь.
Ответ: 4,9 м/с2
m1 
m2
Билет 7.
1. В каком движении участвуют грузы при выключении магнита? Как меняется их движение при прохождении одним из грузов первой платформы? Напишите уравнения этих движений и постройте графики зависимости скорости от времени.
2. Чему равен вес человека, который равноускоренно начал опускаться в лифте с ускорением 1 м/с2? Масса человека 70 кг.
Ответ: 616 Н.
Билет 8.
1. Сформулируйте 3 – й закон Ньютона. Чем отличается сила тяжести от веса тела?
2.Уравнение движения тела имеет вид: x = (5t + 0,8t2) м. Определить среднюю скорость в интервале времени от 2 с до 5 с.
Ответ: 10,6 м/с.
Билет 9.
1. Во второй части работы проверялось соотношение F1t1:F2t2:F3t3 = V1:V2:V3. Откуда оно следует? Как осуществлялось изменение силы F? Какое условие должно было соблюдаться при этом?
2. Тело брошено горизонтально с некоторой высоты со скоростью 20 м/с. Каково перемещение этого тела в пространстве за 2 с от начала движения?
Ответ: 44,5 м.
Билет 10.
1. Как в работе проверялось соотношение S1:S2:S3 = t12:t22:t32? Откуда оно следует?
2. Тело массой 2 кг брошено вертикально вверх со скоростью V0 = 10 м/с. На какую максимальную высоту оно поднимется если 1) трением о воздух пренебречь; 2) трение о воздух равно 5 Н?
Ответ: 5,1 м; 4,1 м.
Билет 11.
1. Что называется импульсом материальной точки? Какая величина называется импульсом системы? Сформулируйте основной закон динамики для материальной точки?
2. Уравнение движения тела имеет вид: x = (0,5t4 – 27t2) м. Через сколько времени после начала движения ускорение тела станет равно 6 м/с2?
Ответ: 3,2 с.
Билет 12.
1. В каком движении участвуют грузы при выключении магнита? Напишите уравнение этого движения и дайте определение величин, которые в него входят. Постройте графики зависимости координаты от времени и скорости от времени для этого вида движения.
2. Небольшой ящик тянут за веревку по гладкой поверхности (без трения). Веревка натянута под углом 45°к направлению движения. Определить величину приложенной силы, если она придает ящику ускорение 0,5 м/с2, масса ящика 2 кг.
Ответ 1,4 Н.
Билет 13.
1. Дайте определение массы и веса, назовите единицы их измерения в системе СИ. Какую величину мы измеряем, вставая на напольные весы?
2. Мяч брошен с некоторой высоты горизонтально со скоростью 15 м/с. Найти нормальное и тангенциальное ускорения мяча через одну секунду после начала движения. Сопротивление воздуха не учитывать.
Ответ: 8,2 м/с2; 5,4 м/с2
Билет 14.
1. Какой закон динамики материальной точки называется основным? Как в работе 2 осуществлялась его проверка?
2. Тело движется вдоль оси X так, что зависимость координаты от времени задано уравнением x = (6 – 3t + 2t2) м. Найти средние скорость и ускорение тела за промежуток времени от 2 до 4 с.
Ответ: 9 м/с; 4 м/с2
Билет 15.
1. Для проверки основного закона динамики используется соотношение F1t1:F2t2:F3t3 = V1:V2:V3. Из какого уравнения находились скорости V1, V2, V3? Откуда оно следует?
2. Автомобиль массой 1 т поднимается по шоссе с уклоном 30° под действием силы тяги 7 кН. Найти ускорение автомобиля, если коэффициент трения равен 0,1.
Ответ: 1,2 м/с2
ЛАБОРАТОРНАЯ РАБОТА 5
ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА
МАЯТНИКЕ ОБЕРБЕКА
Билет 1.
1.Как в лабораторной работе осуществлялась проверка соотношения М1/М2 =e1/e2?
2. Шкив диаметром 20 см делает 300 оборотов за 5 мин. Определить период вращения шкива, угловую и линейную скорости на ободе шкива.
Ответ: 1с; 
6,28 рад/с; 
0,628 м/с.
Билет 2.
1. Как связаны линейные и угловые скорости и ускорения точки, движущейся по окружности?
2. Найти радиус вращающегося колеса, если известно, что линейная скорость точек, лежащих на ободе, в 2,5 раза больше линейной скорости точек, лежащих на 5 см ближе к оси колеса.
Ответ: 8,3 см.
Билет 3.
1.Напишите зависимость угла поворота и угловой скорости от времени при равноускоренном и равнозамедленном движении материальной точки по окружности.
2. Нарисуйте вектор тормозящей силы, действующей на
обод вращающего колеса, и постройте вектор момента
этой силы относительно точки О, лежащей на оси
вращения колеса.
Билет 4.
1. Запишите основной закон динамики для твердого тела, вращающегося вокруг неподвижной оси.
2. Вал начинает вращаться и за первые 10 с совершает 50 оборотов. Считая вращение вала равноускоренным, определите угловое ускорение и угловую скорость вала через 10 с после начала вращения.
Ответ: » 6,28 рад/с2; » 62,8 рад/с
Билет 5.
1. Как в работе рассчитывались моменты инерции дополнительных грузов Iг1, Iг2?
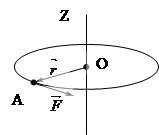
2. Точка А вращается равноускоренно под действием силы 
.
Показать направление момента силы
относительно точки О, лежащей на оси вращения, и
направления векторов d 
, 
и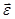 
точки А. Написать
уравнение движения точки А.
Билет 6.
1. Как в работе рассчитывалось линейное ускорение опускающегося груза и угловое ускорение крестовины?
2. Колесо при вращении имеет начальную частоту 5 с –1 , после торможения в течение 10 с частота уменьшилась до 3 с –1 . Найти угловое ускорение колеса и число оборотов, сделанных за время торможения.
Ответ: »1,256 рад/с2; 40
Билет 7.
1. Как в работе рассчитывается момент силы, действующей на крестовину, относительно оси вращения крестовины?
2. Точка А вращается равнозамедленно по окружности
в направлении, указанном стрелкой.
Показать направление угловой и линейной скорости,
а также углового и линейного ускорения точки А.
Написать уравнение движения точки А.
Билет 8.
1. Как в работе рассчитывается угловое ускорение крестовины?
2. Построить вектор линейной скорости и линейного
ускорения точки А, вращающейся по окружности
с центром в точке О, если на рисунке показано
направление угловой скорости точки А. Движение
точки А – ускоренное.
Билет 9.
1. Как будет изменяться момент инерции крестовины с дополнительными грузами, если грузы переместить дальше от оси вращения?
2. Построить вектор момента импульса (относительно точки
О) материальной точки А, вращающейся по окружности
с центром в точке О в направлении, указанном стрелкой.
Написать уравнение движения точки А, считая движение
равнозамедленным.
Билет 10.
1. Как рассчитывается момент импульса твердого тела, вращающегося вокруг неподвижной оси?
2.Колесо вращается по закону j = А + Bt – Ct3, где А = 4 рад, В = 5 рад/с,
С = 1 рад/с3. Найти для момента времени t = 1 с угловую скорость колеса, линейную скорость и полное ускорение точек, лежащих на ободе колеса. Радиус колеса 2 см.
Ответ: 2 рад/с; 0,04 м/с; 0,14 м/с2
Билет 11.
1. Как рассчитывается момент силы относительно точки и относительно оси? Под действием момента какой силы вращалась крестовина при опускании груза?
2. Зависимость угловой скорости от времени для вращающегося тела имеет вид w = A + Bt, где А = 2 рад/с, В = 0,5 рад/с2. Найти полное число оборотов, совершенное телом за 20 с после начала вращения.
Ответ: 22 оборота.
Билет 12.
1.Как рассчитывают момент импульса материальной точки относительно неподвижной точки и момент импульса твердого тела относительно не- подвижной оси?
2. Материальная точка движется по окружности радиусом 81 см согласно уравнению S = At3, где А = 2 м/с3. В какой момент времени нормальное ускорение точки будет равно тангенциальному? Чему будет равно полное ускорение точки в этот момент времени?
Ответ: 0,65 с; 11 м/с2
Билет 13.
1. Как рассчитывается момент инерции материальной точки, твердого тела? Сформулируйте теорему Штейнера.
2. Колесо вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.
Ответ: 3,2 рад/с2
Билет 14.
1. Как формулируется основной закон динамики для тела, вращающегося относительно неподвижной точки, неподвижной оси?
2. Материальная точка движется по окружности радиусом 20 см с постоянным тангенциальным ускорением 5 см/с2. Через сколько времени после начала движения нормальное ускорение точки будет равно тангенциальному?
Ответ: 2 с.
Билет 15.
1. Рассчитайте по результатам лабораторной работы момент импульса крестовины (без дополнительных грузов) относительно ее оси вращения в момент касания грузом пола, если леска наматывалась на малый шкив.
2. Маховик, момент инерции которого равен 63,5 кг×м2, вращается с постоянной угловой скоростью 31,4 рад/с. Найти момент тормозящей силы, под действием которого маховик останавливается через 20 с.
Ответ: 100 Н×м
ЛАБОРАТОРНАЯ РАБОТА 10
ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОГО ДЕКРЕМЕНТА ЗАТУХАНИЯ И ПРИВЕДЕННОЙ ДЛИНЫФИЗИЧЕСКОГО МАЯТНИКА
Билет 1.
1. Выведите формулу для периода колебаний математического маятника.
2. Найти максимальную скорость и максимальное ускорение материальной точки, колеблющейся по закону x = 2 sin (pt / 4 + p / 4) см.
Ответ: 1,57 см/с; 1,23см/с2
Билет 2.
1. Напишите уравнение свободных гармонических колебаний и его решение.
2. Определите амплитуду, период и путь, проходимый колеблющейся материальной точкой за время 1/48 с от начала движения, если колебания происходят по закону x = 10 sin (8pt + p / 6) см.
Ответ: 10 см; 0,25 с; 3,7 см.
Билет 3.
1. Какими параметрами характеризуются затухающие колебания?
2. Логарифмический декремент затухания математического маятника равен 0,2. Во сколько раз уменьшится амплитуда колебаний за время одного колебания маятника?
Ответ: 1,22.
Билет 4.
1. Как рассчитывается приведенная длина физического маятника?
2. На пружине подвешен груз массой 10 кг. Определить период вертикальных колебаний груза, если известно, что под действием груза массой 1 кг пружина растягивается на 0,5 см.
Ответ: 0,4 с.
Билет 5.
1. Нарисуйте график затухающих колебаний. Какие параметры таких колебаний Вы определяли в работе?
2. Амплитуда затухающих колебаний математического маятника за первую минуту уменьшилась в два раза. Во сколько раз она уменьшится за 3 минуты от начала колебаний?
Ответ: в 8 раз.
Билет 6.
1. Напишите уравнение вынужденных колебаний и его решение.
2. Начальная фаза свободного гармонического колебания материальной точки равна нулю. Через какую долю периода скорость колеблющейся точки будет равна половине ее максимальной скорости? Колебания совершаются по закону синуса.
Ответ: 1/6.
Билет 7.
1. Вывести формулу для периода колебаний пружинного маятника.
2. Чему равен логарифмический декремент затухания математического маятника с длиной нити 1м, если за 1 минуту амплитуда колебаний уменьшилась в два раза?
Ответ: 0,023.
Билет 8.
1. Вывести формулу для периода колебаний физического маятника.
2. Амплитуда гармонических колебаний материальной точки равна 2 см, полная энергия колебаний 3 · 10-7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила 2,25 · 10-6 Н?
Ответ: 1,5 мм.
Билет 9.
1. Вывести формулу, связывающую логарифмический декремент и коэффициент затухания.
2. Записать уравнение свободных гармонических колебаний, если известно, что амплитуда колебаний 5 см, период равен 4 с, начальная фаза равна нулю. Найти амплитуду скорости и ускорения. Колебания совершаются по закону синуса.
Ответ: х = 5 sin(pt / 2) см; »7,85 см/с; »12,3 см/с2
Билет 10.
1. Как изменится период затухающих колебаний физического маятника, если закрепить тормозящую пластину выше ее первоначального положения?
2. Материальная точка массой 10 г колеблется по закону x = 5 sin(wt) см. Период колебаний равен 5 с. Найти максимальную силу, действующую на эту материальную точку, и полную энергию колебания.
Ответ: 0,8 мН; 20 мкДж.
Билет 11.
1. Как связана частота собственных колебаний с частотой затухающих колебаний?
2. Период свободных гармонических колебаний равен 5 с, начальная фаза p/5. Чему равна фаза колебания в момент времени 4 с?
Ответ: 9p/5 рад.
Билет 12.
1. Что называется резонансом? Вывести формулу для резонансной амплитуды.
2.Амплитуда синусоидальных гармонических колебаний 10 см, период 12 с, начальная фаза равна нулю. Найти смещение, скорость и модуль ускорения колеблющегося тела через 3 с после начала колебаний.
Ответ: 10 см; 0; 2,7 см/с2
Билет 13.
1. Вывести формулу для определения резонансной частоты колебаний.
2. Материальная точка совершает гармонические колебания. Максимальная скорость точки 10 см/с, максимальное ускорение 100см/с2. Найти циклическую частоту, период колебаний и амплитуду.
Ответ: 10 с –1 ; »0,628 см; 1см.
Билет 14.
1.Чему равен сдвиг фаз колебаний физического и математического маятников при резонансе?
2. Уравнений колебаний точки задано в виде x = sinwt, период Т = 12 с. Найти моменты времени, в которые достигаются максимальная скорость и максимальное ускорение.
Ответ: 6·n с; 3(2n + 1) c, n = 0,1,2,3 …
Билет 15.
1. Какой физический смысл имеет логарифмический декремент затухания?
2. Период собственных колебаний пружинного маятника равен 0,55 с. В вязкой среде период затухающих колебаний этого же маятника стал равным 0,56 с. Определить резонансную частоту nрез колебаний.
Ответ: 1,75 Гц.
СПИСОК ЛИТЕРАТУРЫ
1. Савельев И.В. Курс общей физики в 3т., т.2, т.3 – М.: Наука, 1982
2. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа,1999.
3. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Физматлит, 2001.
4. Волькенштейн В.С. Сборник задач по общему курсу физики. – М.: Наука, 1979.
5. Сборник заданий для индивидуальной самостоятельной работы студентов ФАО и групп очно- заочной формы обучения / Под ред. В.В. Соковишина и Л.В. Спиридоновой МГУПП. – М.: МГУПП, 1997.
6. Лабораторный практикум по механике и молекулярной физике./ Под ред. Л.В. Спиридоновой – М.: МГУПП, 2002.
СОДЕРЖАНИЕ
Лабораторная работа 1. Определение плотности тел правильной геометрической формы........3
Лабораторная работа 2. Исследование законов поступательного движения
и проверка основного закона динамики.....7
Лабораторная работа 5. Изучение законов вращательного движения на маятнике Обербека.........12
Лабораторная работа 10. Определение логарифмического декремента затухания и приведенной длины физического маятника..17
СОСТАВИТЕЛИ
Лабораторные работы №1 и №2 – к.т.н. доцент Спиридонова Л.В.
Лабораторные работы №5 и №10 – к.физ.-мат.н. доцент Соковишин В.В.