1.Найти собственные значения матрицы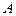 
методом вращения с точностью 
.
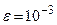Матрица 
.
Элементы матрицы 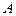представляются в виде многочлена от параметра 
по схеме Горнера следующим образом:
:
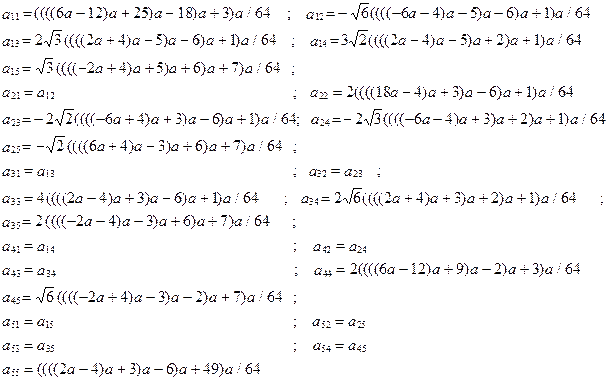
Положим параметр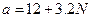 
.
2.Используя найденные собственные значения матрицы 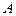из 1 пункта настоящего задания найти методом обратных итераций с точностью 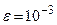собственные вектора этой матрицы .
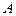3.Используя вычисленные собственные значения матрицы 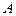, вычислить число обусловленности 
матрицы ( =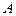 
?).
4.Найти методом Данилевского собственные значения матрицы с точностью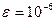 
.
Элементы исходной матрицы имеют вид:
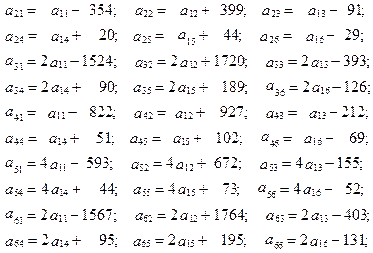
Положим параметр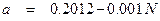 
.
Решение.
Метод вращений Якоби применим только для симметрических матриц 
(
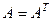) и решает полную проблему собственных значений и собственных векторов таких матриц. Он основан на отыскании с помощью итерационных процедур матрицы 
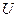в преобразовании подобия 
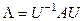, а поскольку для симметрических матриц матрица преобразования подобия 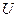является ортогональной (
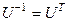), то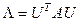 
,
где 
- диагональная матрица с собственными значениями на главной диагонали
.
Пусть дана симметрическая матрица A. Требуется для нее вычислить с точностью 
все собственные значения и соответствующие им собственные векторы. Алгоритм метода вращения следующий:
Пусть известна матрица 
на k –й итерации, при этом для k =0 
.
1. Выбирается максимальный по модулю недиагональный элемент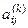 
матрицы (
= 
).
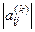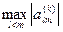2. Ставится задача найти такую ортогональную матрицу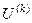 
, чтобы в результате преобразования подобия 
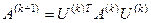произошло обнуление элемента 
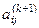матрицы 
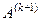. В качестве ортогональной матрицы выбирается матрица вращения, имеющая следующий вид:
,
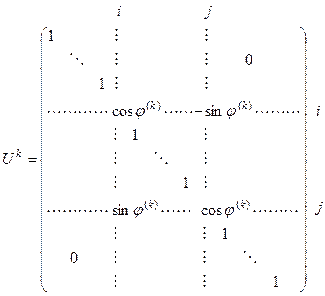В матрице вращения на пересечении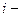 
й строки и 
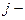го столбца находится элемент 
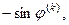где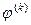 
- угол вращения, подлежащий определению. Симметрично относительно главной диагонали (
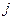-я строка, 
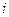-й столбец) расположен элемент 
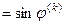; Диагональные элементы 
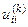и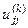 
равны соответственно 
, 
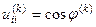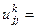
; другие диагональные элементы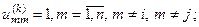 
остальные элементы в матрице вращения 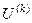равны нулю.
Угол вращения 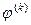определяется из условия 
:
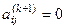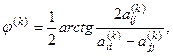
причем если 
то 
.
3. Строится матрица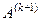
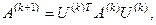
в которой элемент 
В качестве критерия окончания итерационного процесса используется условие малости суммы квадратов внедиагональных элементов:
Если 
то итерационный процесс
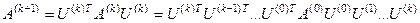
продолжается. Если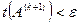 
, то итерационный процесс останавливается, и в качестве искомых собственных значений принимаются 
.
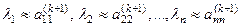Координатными столбцами собственных векторов матрицы в единичном базисе будут столбцы матрицы 
т.е.
причем эти собственные векторы будут ортогональны между собой, т.е. 
|
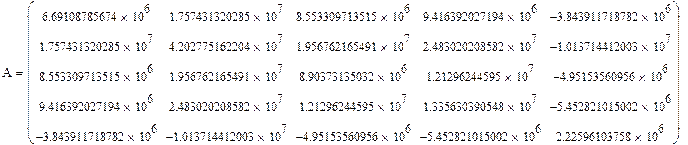
Исходная матрица имеет следующий вид:
|
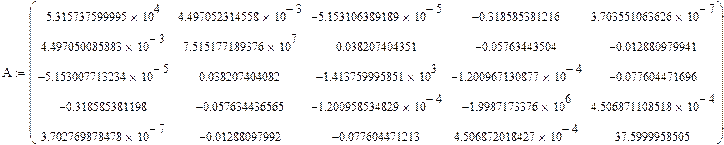
Полученная после 26-ти вращений матрица имеет следующий вид:
При этом количестве итераций выполняется условие прекращения вращения:
|
Полученные результаты занесем в таблицу:
| Полученное | Эталонное (MathCAD) | Погрешность |
| 7.515177189376*10^7 | 7.515177189376*10^7 | |
| 5.315737599995*10^4 | 5.3157376*10^4 | 5.000765668228e-8 |
| -1.9987173376*10^6 | -1.9987173376*10^6 | |
| -1.413759995851*10^3 | -1.413760000001*10^3 | 4.149999995207e-6 |
| 37.5999958505 | 37.600000000022 | 4.149521998897e-6 |
2. Во второй части работы необходимо, используя найденные собственные значения матрицы 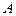из 1 пункта настоящего задания, найти методом обратных итераций с точностью 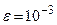собственные вектора этой матрицы 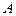. Фиксируем любое 
. Итерации организуются по формуле: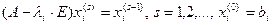 
Полученные результаты занесем в таблицу:
| 
| 
| 
| 
|
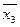
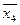
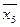
| 0.306186402836609 | -0.4329868554455 | 0.62499726777906 | -0.530202717044 | 0.21650309427297 |
| 0.750000169758517 | 0.3535860194924 | 0.306437647186 | 0.43301579317868 | -0.1767665974995 |
| 0.353553521374879 | 0.49999996670825 | -0.4329604571284 | -0.6124079341296 | 0.249993792793697 |
| 0.433012864743218 | -0.6123362370203 | -0.530147425534 | 0.249668630787 | 0.306188574186227 |
| -0.17677670008803 | 0.25000729108811 | 0.2164862520481 | 0.30618777250429 | 0.875002942355846 |
Эталонные (MathCAD) значения занесем в следующую таблицу:
|
|
|
|
|
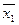
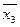
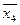
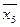
| 0.30618622 | -0.43301269 | 0.62500011 | -0.53033198 | 0.21650141 |
| 0.75 | 0.35355339 | 0.30618613 | 0.43301437 | -0.17677278 |
| 0.35355339 | 0.5 | -0.43301258 | -0.61237478 | 0.24999447 |
| 0.4330127 | -0.61237244 | -0.53033007 | 0.24999712 | 0.30618858 |
| -0.1767767 | 0.24999999 | 0.21650644 | 0.30617825 | 0.87500277 |
Погрешность вычислений занесем в следующую таблицу:
|
|
|
|
|
|
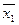
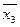
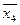
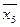
| -0.000000182836609 | -0.0000258345545 | 0.00000284222094 | -0.000129262956 | -0.00000168427297 |
| -0.000000169758517 | -0.0000326294924 | -0.000251517186 | -0.00000142317868 | -0.0000061825005 |
| -0.000000131374879 | 0.00000003329175 | -0.0000521228716 | 0.0000331541296 | 0.000000677206303 |
| -0.000000164743218 | -0.0000362029797 | -0.00018264446 | 0.000328489213 | 0.000000005813773 |
| 0.000000000088037 | -0.00000730108811 | 0.0000201879519 | -0.00000952250429 | -0.00000017235584 |
3. В третьей части задания необходимо используя вычисленные собственные значения матрицы 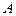, вычислить число обусловленности матрицы ( = ?).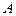
В численных методах, число обусловленности характеризует точность решения задачи и является мерой усреднимости этого решения в численном представлении, то есть насколько задача хорошо или плохо обусловлена.
Если число обусловленности некоего уравнения мало́, то уравнение называется хорошо обусловленным. Если же число обусловленности велико, то уравнение называется плохо обусловленным.
С числом обусловленности связано множество утверждений и оценок теории вычислительной математики.
Для симметричных матриц число обусловленности матрицы A равно отношению максимального собственного числа к минимальному числу. Пользуясь этим определением и ранее полученными данными определяем данное отношение:
|
В четвертой части задания нужно найти методом Данилевского собственные значения матрицы с точностью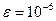 
.
Для этого всего лишь на всего нам нужно привести нашу исходную матрицу к нормальному виду Фробениуса. Матрица Фробениуса имеет вид:
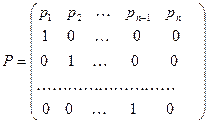
Согласно методу Данилевского переход от матрицы к ей подобной матрице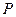 
осуществляется с помощью 
преобразований подобия, последовательно преобразующих строки матрицы , начиная с последней.
Исходная матрица имеет вид:
|
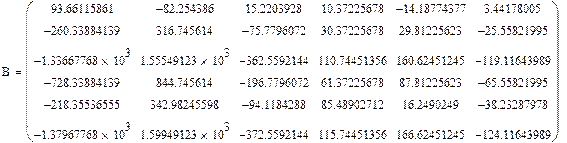
Приведенная к нормальной форме Фробениуса матрица имеет вид:
|
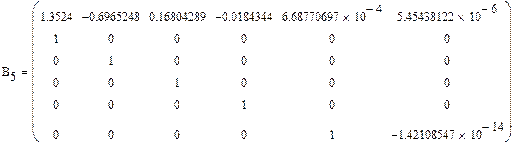
Отсюда мы получаем формулу для характеристического многочлена:
Находим корни данного многочлена, результаты заносим в таблицу:
| Полученное | Эталонное (MathCAD) | Погрешность |
| 0.393198928 | 0.393198777 | 0.000000151650 |
| 0.386401235 | 0.386401195 | 0.000000039699 |
| 0.293199705 | 0.293199594 | 0.000000110357 |
| 0.1932002 | 0.193200131 | 0.000000069238 |
| 0.093199918 | 0.093199565 | 0.000000353742 |
| 0.393198928 | 0.393198777 | 0.000000151650 |
Вывод:
Метод вращения Якоби очень удобен, но существенным недостатком является то, что он применим только для симметричных матриц. Реализация описанного варианта метода вращения требует выбора максимального по модулю внедиагонального элемента матрицы на каждом шаге. Для выполнения этой операции на ЭВМ требуется значительный объем вычислительной работы.
Метод обратных итераций дает хорошую точность уже после одной итерации с использованием значений, которые мы изначально получили с какой-то погрешностью.
Число обусловленности имеет большое значение для определении устойчивости решения системы линейных уравнений, определяемых данной матрицей, при изменении начальных данных.
Во время освоения данного метода мы не могли пропустить некоторые минусы метода Данилевского:
- Погрешность накапливается со скоростью геометрической прогрессии.
- Приходится решать достаточно сложное уравнение порядка n (если решать с помощью приближенных метод, снова получаем некоторую погрешность)
- В программном варианте используются достаточно большие объемы оперативной памяти, к примеру, приходится хранить до 4 матриц порядка n*n.
Но так же нельзя не остановиться на очевидных плюсах метода:
- Метод удобен для нахождения собственных векторов практически любой матрицы. Рекомендуется рассматривать матрицы меньше порядка нескольких десятков.
- Данный метод очень удобен в программировании (на этапе разработки ПО проблем практически не возникало).
В целом метод все-таки не рекомендуется для решения задач, требующих высоких точностей. Но из-за своей простоты, и высокой скорости, подходит для больших массивов, не требующих отсутствие погрешности.