Порядок работы с приложением РАС-Designer

К выполнению лабораторных работ в интерактивной форме

(методические рекомендации по проведению компьютерного моделирования с демонстрацией процесса на интерактивной доске) для студентов

специальности

 

23.05.05 СИСТЕМЫОБЕСПЕЧЕНИЯ ДВИЖЕНИЯ ПОЕЗДОВ

 

Москва – 2015г.

 

Составитель – к.т.н., доц. Панков Ю.Н.

 

Рецензент – к.т.н, доц. Цуцков В.В.

 

 

ЛАБОРАТОРНАЯ РАБОТА № 1

 

ИССЛЕДОВАНИЕ ПЕРЕДАТОЧНЫХ ЧАСТОТНЫХ

ХАРАКТЕРИСТИК В ЦЕПЯХ ПЕРВОГО ПОРЯДКА

 

ЦЕЛЬ РАБОТЫ

Экспериментально и расчетным путем получить передаточные амплитудно-частотные (АЧХ) и фазо-частотные (ФЧХ) характеристики про­стейших цепей.

 

КРАТКИЕ ПОЯСНЕНИЯ

Комплексным коэффициентом передачи по напряжению в общем случае называется отношение комплексного выходного напряжения к комплексному входному напряжению . Совокупность коэффициентов передачи на различных частотах называется комплексной передаточной функцией (КПФ) . Комплексная передаточная функция состоит из двух характеристик – амплитудно-частотной и фазо-частотной . Чтобы рассчитать КПФ, в общем случае не­обходимо:

1) задаться произвольным напряжением на входе четырехпо­люсника U₁;

2) любым методом рассчитать ток (или токи) в элементе (или
элементах), с которого снимается выходное напряжение;

3) зная ток (токи) и сопротивление выходного элемента (эле­ментов), рассчитать комплексное выходное напряжение ;

4) рассчитать комплексную передаточную функцию из выражения и записать ее в показательной форме . В этой функции модуль Н и аргумент являются члена­ми, зависящими от частоты ;

5) записать выражение передаточной амплитудно-частотной характеристики (передаточной АЧХ), и передаточной фазо-частотной характеристики (передаточной ФЧХ), .

Таким образом, кривая, по которой изменяется модуль ком­плексной передаточной функции в зависимости от частоты, есть передаточная АЧХ, а кривая, по которой изменяется аргумент комплексной передаточной функции, – передаточная ФЧХ.

В цепях Г-образного вида (рис. 1.1 а), , на­пример, в цепи (рис. 1.1 б)

откуда

 

А) б)

 

в) г)

Рис. 1.1

Кривые и показаны на рис. 1.1, б и г. Легко видеть, что при . В RL – цепи (рис. 1.2, а)

откуда

(рис. 1.2, б),

(рис.1. 2, в).

На граничной частоте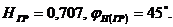

а)

б) в)

Рис. 1.2

В неразветвленных цепях с одним накопителем энергии удобно пользоваться понятием – граничная частота . Граничной называется частота, при которой модуль реактивного сопротивления равен резистивному сопротивлению, т.е. в RL-цепях 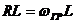, откуда а в RC-цепях откуда

 

Расчет резистивно-емкостной цепи

 

1. Рассчитать передаточные цепи АЧХ и ФЧХ цепи рис. 1.1, б в диапазоне 2…14 кГц через интервалы 2 кГР, если R = 100 ОМ, С = 0,2 МкФ. Результаты расчетов занести в тбл. 1.

2. Нанести на график кривые и , полученные по предварительному расчету.

3. Рассчитать граничную частоту.

Таблица 1

 

При

 

ЗАДАНИЕ

Экспериментально получить передаточные амплитудно-частотные и фазо-частотные характеристики: активного фильтра по программе PАK-10.

 

Порядок работы с приложением РАС-Designer

1. Запустить приложение по ярлыку, расположенному на рабочем столе или меню Пуск->Программы;

2. Выбрать демонстрационный пример (File->Browse Library..) ispPAC10_XXX или ispPAC20_XXX по заданию преподавателя. На дисплее появится схема внутренних соединений данного типа микросхемы.

3. Изменить схему согласно данному преподавателем заданию.

4. Построить ФЧХ и АЧХ синтезируемой семы Tools->Run Simulator

5. Изменить параметры схемы для достижения заданной цепи и повторить п. 4.