КУРСОВОЙ ПРОЕКТ
(пояснительная записка)
по дисциплине: Механика машин и теория колебаний
на тему: Анализ и синтез плоских механизмов
Исполнитель – студент уч. группы
(Фамилия, И., О., подпись)
Руководитель
(Ученая степень, звание, Фамилия, И., О., подпись)
Оценка
Санкт-Петербург
Г.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Санкт-Петербургский государственный университет
промышленных технологий и дизайна»
Кафедра машиноведения
ЗАДАНИЕ НА КУРСОВОЙ ПРОЕКТ (РАБОТУ)
Студенту
группы
Тема проекта (работы)
Содержание задания
Задача проекта (работы)
Исходные данные:
а) технологические параметры:
б) конструктивные параметры:
в) особые условия:
г) объем проекта (работы):
Пособия и рекомендуемые материалы:
Дата выдачи задания:
Сроки выполнения задания:
Подготовительный этап (срок):
Пояснительная записка (количество листов и содержание)
Перечень графического материала (с точным указанием обязательных чертежей)
.
Руководитель: ________________________
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
Санкт-Петербургский государственный университет промышленных технологий и дизайна
Кафедра машиноведения
|
Группа _____ 3-МЗ-2 «С» _____ Дата выдачи работы __ сентябрь __ 2017 г.
|

|
входного звена
n 1 = 4,84 с–1.
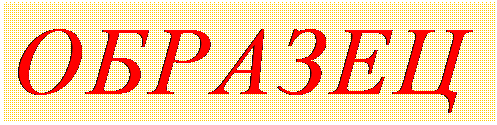
Содержание работы:
Лист 1. Кинематический анализ рычажного механизма (6+6+3).
Лист 2. Кинетостатический (силовой) анализ рычажного механизма (2+2 РЖ).
Лист 2. Синтез кулачкового механизма.
Таблица 1
Параметры рычажного механизма, м
| 01А | АВ | АС | О1D | CЕ | 01 s 1 | А s 2 | С s 4 | |||||||||
| 0,05 | 0,16 | 0,06 | 0,17 | 0,2 | 0,02 | 0,02 | 0,1 | |||||||||
| Массы звеньев, кг | Моменты инерции (динамические моменты инерции), кг·м2 | |||||||||||||||
| m 1 | m 2 | m 3 | m 4 | m 5 | Js 1 | Js 2 | Js 3 | Js 4 | Js 5 | |||||||
| – | – | – | – | – | – | – | – | – | – | |||||||
Таблица 2
Параметры кулачкового механизма
| Номер варианта | Тип механизма | Размеры кулачкового механизма, мм | Углы поворота кулачка, град | ||||||||
| r 0 | ρ | е | Х | Y | L | Smax (βш) | Рабочий ход, φш, рх | Дальний выстой, φдв | Холостой ход, φш, хх | ||
| А | – | – | – |
Таблица 3
Законы безразмерного ускорения ведомого звена; параметры зубчатой пары
| Рабочий (прямой) ход (РХ) | Холостой (обратный) ход (ХХ) | Зубчатая пара | ||||||||||||
| Разбег | Выбег | λрх | δβрх | Разбег | Выбег | λхх | δβхх | z 1 | z 2 | m, мм | ||||
| S 1 | S 2 | S 1 | S 2 | S 1 | S 2 | S 1 | S 2 | |||||||
| 0,4 | 0,3 | 0,2 | 0,2 | 1,7 | 0,35 | 0,4 | 0,6 | – | – | – |
Типы кулачковых механизмов

|
СОДЕРЖАНИЕ
1 Задание на курсовой проект (работу)............. 2
Введение......................... 5
2 ОСНОВНАЯ ЧАСТЬ
ЛИСТ № 1.Кинематическое исследование
плоского рычажного механизма.................. 6
ЛИСТ № 2 Кинетостатическое (силовое) исследование
плоского рычажного механизма.................. 16
ЛИСТ № 3. Синтез профиля кулачка в кулачковом механизме... 17
3 ЗАКЛЮЧЕНИЕ...................... 30
4 Список использованных литературных источников........ 31
ВВЕДЕНИЕ
Представленная для исследования механическая система включает в себя: 1. Рычажный механизм (подлежащий разработке студентами заочной формы обучения);
2. Кулачковый механизм (подлежащий разработке студентами заочной формы обучения);
3. Зубчатый механизм (не подлежащий разработке студентами заочной формы обучения).
По условиям выполнения курсовой работы исследование рычажного механизма заключается в кинематическом анализе этого механизма. Графическая часть работы – 1 лист формата А1 (оформленный с учетом требований ЕСКД), содержащий 6 планов положений рычажного механизма, 6 планов его скоростей, 3 плана его ускорений.
Пояснительная записка содержит основные расчетные зависимости и ком-ментарии по этой теме.
В отдельных случаях студентами выполняется кинетостатическое (силовое) исследование плоского рычажного механизма – лист 2 формата А1.
Синтез профиля кулачка с применением аппарата безразмерных характеристических функций в кулачковом механизме – 3-й лист выполняемого курсового проекта. Графическая часть работы – 1 лист формата А1 (оформ-
ленный с учетом требований ЕСКД), содержащий в прямоугольной координатной системе диаграммы функции положения, первой и второй передаточных функциях выходного звена механизма. На второй половине этого же листа изображаются профили кулачка (теоретический и практический) в полярной координатной системе; здесь же (на участках I-II и V-VI теоретического профиля) строятся углы давления и их фактические значения сравниваются с допустимыми. По результатам сравнений делаются выводы о работоспособности выполненного профиля кулачка.
Пояснительная записка содержит основные расчетные зависимости и комментарии по этой теме.
С учетом направления подготовки и формы обучения кинетостатическое (силовое) исследование параметров рычажного механизма и геометрии (кинематики) зубчатого механизма не вошли в перечень предложенных к рассмотрению тем.
ОСНОВНАЯ ЧАСТЬ
ЛИСТ № 1
Кинематическое исследование плоского рычажного механизма
Исходные данные (выбираются в соответствии с № зачетной книжки или задаются преподавателем):
– схема механизма с размерами звеньев;
– частота вращения входного (ведущего) звена n 1 = 4,84 с-1;
– направление вращения входного звена – против часовой стрелки.
Перед началом выполнения кинематического исследования необходимо проверить предложенный механизм на работоспособность. Для этого определим его степень подвижности относительно стойки. Используем формулу Чебышева
 = 3·5 – 2·7 = 1.
= 3·5 – 2·7 = 1.
Кинематические пары р 4 (высшие пары) здесь отсутствуют.
Механизм, имеющий одну степень свободы относительно стойки, имеет одновременно только одно входное звено [1].
От звена, указанного как ведущее, выполним структурный анализ.
Разделим весь механизм на группы Ассура [2]:
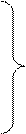 Стойка – О1 – 1. Это начальный механизм, имеющий W = 1.
Стойка – О1 – 1. Это начальный механизм, имеющий W = 1.
А вр – В вр – В пост. Это ведомая цепь II класса, 2-го порядка,
2-й модификации, имеющая W = 0. (1)
С вр – D пост – D вр. Это ведомая цепь II класса, 2-го порядка,
3-й модификации, имеющая W = 0.
Класс групп Ассура определяется соотношением:
n – количеством подвижных звеньев в группе;
р 5 – количеством кинематических пар 5-го класса.
Порядок кинематической пары – числом вакантных связей (в цепи второго класса – группе Ассура их всегда две).
Цепь второго класса всегда имеет n = 2, р 5 = 3.
Модификация определяется соотношением вращательных и поступательных кинематических пар (КП).
1-я модификация имеет Вр – Вр – Вр кинематические пары (ВВВ);
2-я модификация имеет Вр – Вр – Пост (ВВП) или Пост – Вр – Вр (ПВВ) кинематические пары;
3-я модификация имеет Вр – Пост – Вр (ВПВ) кинематические пары;
4-я модификация имеет Пост – Вр – Пост (ПВП) кинематические пары;
5-я модификация имеет Вр – Пост – Пост (ВПП) или Пост – Пост – Вр (ППВ) кинематические пары.
В выражении 1 неизвестную скорость (·) В вр определим через известные скорости точек А и В пост [3].

 (2)
(2)
Вектор скорости V А направим ┴ 1 звену – кривошипу в сторону его вращения.
Модуль скорости V А (численное значение) определим из выражения
 2·π· n 1·О1А = 2·3,14·4,84·0,05 = 1,519 м/с.
2·π· n 1·О1А = 2·3,14·4,84·0,05 = 1,519 м/с.
Направление вектора скорости V А нам неизвестно, но ввиду того, что при вращении входного звена – кривошипа (·) В вращается относительно (·) А, линию действия относительной скорости V В2,3А направим 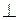 АВ (звену 2).
АВ (звену 2).
(·) В, находящаяся на стойке, имеет нулевую скорость, следовательно  .
.
Направление вектора скорости  нам также неизвестно, однако известно, что при вращении кривошипа ползун или (·) В 3 перемещается поступательно относительно (·) В, принадлежащей стойке, т.е. (·) В ст. Линия действия при этом поступательном движении направляется вдоль движения ползуна, т.е. ║ направляющей х-х.
нам также неизвестно, однако известно, что при вращении кривошипа ползун или (·) В 3 перемещается поступательно относительно (·) В, принадлежащей стойке, т.е. (·) В ст. Линия действия при этом поступательном движении направляется вдоль движения ползуна, т.е. ║ направляющей х-х.
В соответствии с системой векторных уравнений (2) выполним построение векторов в указанной последовательности, учитывая масштабный коэффициент (масштаб плана скоростей) μV.
Для этого определим соотношение истинной линейной скорости и соответствующего этой скорости отрезка на плане скоростей, т. е.
 м/с мм.черт.
м/с мм.черт.
Величину вектора скорости  выберем произвольно исходя из того, чтобы значение масштабного коэффициента μv получить в виде короткой цифры.
выберем произвольно исходя из того, чтобы значение масштабного коэффициента μv получить в виде короткой цифры.
Все построения начнем из некоторой начальной точки, обозначений на чертеже как полюс плана скоростей Рv.
Следующую систему векторных уравнений для определения неизвестной скорости (·) D 4 запишем аналогичным образом.

 (3)
(3)
Неизвестную на данный момент скорость (·) С на плане скоростей определим исходя из пропорционального соотношения длин отрезков АВ и АС, взятых с механизма и отрезков (аb)v и (ас)v, взятых на плане скоростей.
Вариант пропорции запишем в виде
АС / АВ = (ас)v / (аb)v,
откуда рассчитаем искомое неизвестное:
60 / 160 = (ас)v / 68
или (ас)v = 60·68/160 = 25,5 мм.черт.
Величина (аb)v взята из построенного этапа плана скоростей. Полученное расчетным путем расстояние (ас)v отложим в качестве продолжения отрезка (аb)v в сторону (·) С на плане скоростей.
Направление вектора скорости  нам неизвестно, однако при вращении кривошипа (·) D, принадлежащая 4 звену, вращается относительно (·) С, поэтому линию действия относительной скорости
нам неизвестно, однако при вращении кривошипа (·) D, принадлежащая 4 звену, вращается относительно (·) С, поэтому линию действия относительной скорости  направим
направим 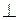 DC (звену 4).
DC (звену 4).
(·) D 5, принадлежащая стойке, имеет скорость, равную нулю, следова-тельно  .
.
Направление вектора скорости 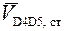 нам также неизвестно, однако при вращении кривошипа ползун или (·) D 5 перемещается поступательно относительно(·) D , принадлежащей кулисе, т. е. (·) D 4. Линия действия относи
нам также неизвестно, однако при вращении кривошипа ползун или (·) D 5 перемещается поступательно относительно(·) D , принадлежащей кулисе, т. е. (·) D 4. Линия действия относи
тельной скорости при этом поступательном движении направляется вдоль движения ползуна, т. е. ║ направляющей CD (звено 4).
В соответствии с системой векторных уравнений (3) выполним построение векторов в указанной уравнениями последовательности в том же масштабе плана скоростей μv.
Построение здесь начнем не из полюса Рv, как в предыдущем случае (система уравнений 2), а из полученной ранее на плане скоростей (·) С.
Неизвестную на плане скоростей (·) Е найдем, используя правило деления отрезков на пропорциональные части.
Вариант пропорции запишем в виде
СD / СЕ = (сd)v / (ce)v,
откуда рассчитаем искомое неизвестное:
148/200 = 120/(ce)v или (се)v = 200·120/148 = 162 мм.черт.
Для определения на плане скоростей (·) С в положениях 2, 4 и 5 запишем пропорции вида:
АС / АВ = (ас)v / (аb)v,
60/160 = (ас)v2,4 / 70, откуда (ас)v2,4 = 26 мм.черт.
60/160 = (ас)v5 / 73, откуда (ас)v5 = 27 мм.черт.
Мгновенные значения угловых скоростей всех звеньев для положения 1 определим из выражений
 с-1;
с-1;
 ;
;
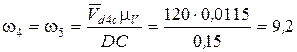 с-1.
с-1.
Мгновенные значения угловых скоростей всех звеньев для положения 5 определим из выражений
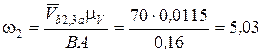 с-1;
с-1;  ;
;
 с-1.
с-1.
Для построения плана ускорений воспользуемся структурой механизма (1).
В структуре механизма неизвестное ускорение (·) В 2,3 определим через известные ускорения (·) А и (·) В ст.

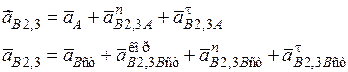 (4)
(4)
Вектор полного ускорения 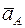 (или
(или  ) направим вдоль кривошипа от (·) А в сторону его центра вращения или (·) О1.
) направим вдоль кривошипа от (·) А в сторону его центра вращения или (·) О1.
Модуль ускорения  (его численное значение) определим из выражения
(его численное значение) определим из выражения
 .
.
При условии ω 1 = const имеем ε 1 = 0, т.е. кривошип вращается равномерно.
Полное ускорение кривошипа будет равно его нормальному ускорению.
Модуль нормальной (центростремительной) составляющей ускорения  определим из равенства:
определим из равенства:
 м/с2.
м/с2.
Длину соответствующего вектора определим из равенства:
 мм.черт.
мм.черт.
Здесь вектор скорости  найдем на плане скоростей в мм.чертежа; μ V – масштаб плана скоростей (м/с мм.черт); ВА – длина звена в истинную величину в м (из задания); μ а – масштаб плана ускорений (м/с2 мм.черт).
найдем на плане скоростей в мм.чертежа; μ V – масштаб плана скоростей (м/с мм.черт); ВА – длина звена в истинную величину в м (из задания); μ а – масштаб плана ускорений (м/с2 мм.черт).
Вектор нормального ускорения направим вдоль звена АВ от шарнира В в сторону шарнира А.
Вектор (его линию действия) касательной (тангенциальной) составляющей ускорения направим 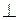 звену АВ.
звену АВ.
(·) В, находящаяся на стойке, имеет нулевое ускорение, следовательно  .
.
Модуль кориолисова ускорения в общем случае определяется из выражения
 м/с2.
м/с2.
Здесь по условию задачи ω3 = 0, поэтому  .
.
Модуль нормального ускорения определим из выражения
 ,
,
где ρх-х – радиус кривизны направляющей, по которой перемещается ползун – звено 3. Здесь направляющая прямолинейна, ρх-х = ∞ и нормальное ускорение рано нулю.
Вектор (линию действия) касательной (тангенциальной) составляющей ускорения 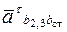 при относительном поступательном движении звена 3 вдоль направляющей х-х проведем ║ этой направляющей CD (л.д. ║ х-х).
при относительном поступательном движении звена 3 вдоль направляющей х-х проведем ║ этой направляющей CD (л.д. ║ х-х).
В соответствии с системой векторных уравнений (4) выполним построение векторов в указанной последовательности с учетом масштабного коэффициента (масштаба) плана ускорений μа
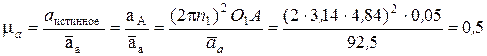 м/с2 мм.черт.
м/с2 мм.черт.
Знаменатель дроби – величину вектора ускорения 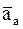 – выбираем произ-вольно исходя из того, чтобы значение масштабного коэффициента μа получить в виде короткой цифры.
– выбираем произ-вольно исходя из того, чтобы значение масштабного коэффициента μа получить в виде короткой цифры.
Для положения I запишем:
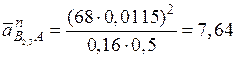 мм.черт.
мм.черт.
На плане ускорений положение (×) С определим из пропорции вида:

 м.
м.
В выражении (1) неизвестное ускорение (×) D 4 определим через известное ускорение точек  и D 5,СТ.
и D 5,СТ.

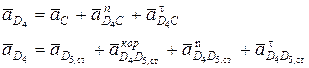 (5)
(5)
Нормальную (центростремительную) составляющую ускорения  определяем из равенства:
определяем из равенства:
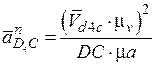 мм.черт.
мм.черт.
Здесь вектор скорости  найдем на плане скоростей в мм.черт.;
найдем на плане скоростей в мм.черт.;  – длина звена в истинную величину – берется из плана механизма, м.;
– длина звена в истинную величину – берется из плана механизма, м.;
Вектор нормального (центростремительного) ускорения направим вдоль звена 4 ( ) от (×) D 4 в сторону шарнира (
) от (×) D 4 в сторону шарнира ( ).
).
Вектор касательной (тангенциальной) составляющей ускорения направляется  звену
звену  в виде линии его действия, т.е. л.д.
в виде линии его действия, т.е. л.д. 
 .
.
(×) D 5, находящаяся на стойке, имеет ускорение, равное нулю, следовательно  .
.
Кориолисово ускорение здесь  и определяется из
и определяется из
 мм.черт.
мм.черт.
После подстановки цифровых значений для положения I имеем:
 мм.черт.
мм.черт.
Нормальное ускорение
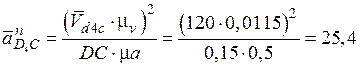 мм.черт.
мм.черт.
Для второго по счету положения плана ускорений выполним расчет необходимых параметров. На ускорениях оно имеет сквозную нумерацию – номер 5.
V положение.
 мм.черт.
мм.черт.
 м.
м.
 мм.черт.
мм.черт.
 мм.черт.
мм.черт.
Направления кориолисова ускорения определим по следующему правилу:
– найдем вектор относительной скорости на плане скоростей ( );
);
– вынесем его на свободное поле чертежа и развернем на 90° по направлению угловой скорости ползуна (звено 4).
Для положения I на плане ускорений эти построения имеют вид:
|

|

Направления угловых скоростей ползунов ( ) определяются по алго-ритму, показанному в [3].
) определяются по алго-ритму, показанному в [3].
Положение (×) Е на плане ускорений можем определить из пропорции вида
 .
.
Передаточные функции рычажного механизма могут быть определены из выражений:
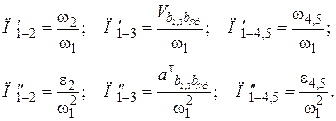 (6)
(6)
Первые и вторые передаточные функции являются переменными по величине и знаку.
ЛИСТ № 2