Египетская нумерация. Египетская нумерация представлена на рис. 3.2. Операции умножения и деления производятся путем последовательного удвоения чисел – фактически представлением числа в двоичной системе.
Римская нумерация. Эта нумерация используется и в настоящее время. С нею мы достаточно часто сталкиваемся в повседневной жизни. Так нумеруются главы в книгах, века, числа на циферблате часов и т.д.
Возникла эта нумерация в Древнем Риме. В ней имеются узловые числа:
– I – 1;
– V – 5;
– X – 10;
– L – 50;
– С – 100;
– D – 500;
– М – 1000;
– Z – 2000.

Остальные числа получаются путем прибавления или вычитания одних узловых чисел из других. Например:
– четыре записывается как IV (т.е. пять минус один);
– восемь – VIII (пять плюс три);
– сорок – XL (пятьдесят минус десять);
– девяносто шесть – XCVI (сто минус десять плюс пять и плюс еще один) и т.д.
В римской записи числа важно не собственно положение цифры, а ее положение относительно другой цифры. Сравните записи XI и IX. Здесь в обоих случаях присутствуют две цифры – I и X, но в одном случае единицу нужно прибавлять к 10, а в другом – вычитать!
Алфавитные нумерации
В середине V в. до н. э, появилась запись чисел нового типа – так называемая алфавитная нумерация. В этой системе записи числа обозначались при помощи букв алфавита, над которыми ставились черточки: первые девять букв обозначали числа от 1 до 9, следующие девять – числа 10, 20, 30,..., 90, и следующие девять – числа 100, 200,..., 900. Таким образом, можно было обозначать любое число до 999.
Древнегреческая нумерация. В древнегреческой нумерации (рис. 3.3) запись алфавитными символами могла делаться в любом порядке, поскольку число получалось как сумма значений отдельных букв. Например, записи blj, ljb и lbj эквивалентны и означают число 532. Здесь jозначает 500, l – 30, b – 2.
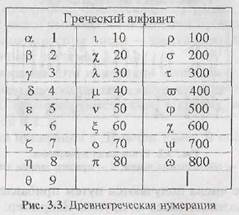
Однако выполнять арифметические вычисления в такой системе было настолько трудно, что без применения некоторых приспособлений оказалось обойтись практически невозможно.
Славянская кириллическая нумерация. Алфавитная система была принята и в Древней Руси (рис. 3.4).

Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. Если посмотреть внимательно, то увидим, что после «а» идет буква «в», а не «б», как следует по славянскому алфавиту, т.е. используются только буквы, которые есть в греческом алфавите. Чтобы различать буквы и цифры, над числами ставился особый значок – титло – (рис. 3.5).

Так можно было записывать числа до 999. Для больших чисел использовался знак тысячи ¹, который ставился впереди символа, обозначавшего число.
До XVII в. эта форма записи чисел была официальной на территории России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. В православных церковных книгах такая нумерация используется до сих пор.
Арабская нумерация. Это самая распространенная нумерация, которой мы пользуемся в настоящее время.
Применяемые в настоящее время цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 появились в Индии около 400 г. Арабы стали пользоваться подобной нумерацией около 800 г., а примерно в 1200 г. ее начали применять в Европе. Однако в Европе такая нумерация стала известна благодаря трудам арабских математиков, и потому за цифрами утвердилось название «арабские», хотя сами арабы вплоть до настоящего времени пользуются совсем другими символами.
В России арабская нумерация стала использоваться при Петре I (до конца XVII в. сохранялась славянская нумерация).
В Древней Индии и Китае существовали системы записи, построенные на мультипликативном принципе. В таких системах для записи одинакового числа единиц, десятков, сотен или тысяч применяются одни и те же символы, но после каждого символа пишется название соответствующего разряда. Если десятки обозначить символом Д, а сотни – С, то число 325 будет выглядеть так: ЗС2Д5.
Из арабского языка заимствовано и слово «цифра» (по-арабски оно звучит как «сыфр»), означающее буквально «пустое место». Это слово применялось для названия знака пустого разряда, и оно сохраняло этот смысл до XVIII в., хотя еще в XV в. появился латинский термин «нуль» (nullum – ничто).
Форма индийских цифр претерпевала многообразные изменения. Та форма, которой мы сейчас пользуемся, установилась в XVI в. По мнению марроканского историка Абделькари Боунжира, арабским цифрам в их первоначальном варианте было придано значение в строгом соответствии с числом углов, которые образуют фигуры.
Системы счисления
Система счисления – совокупность правил наименования и представления чисел с помощью набора символов, называемых цифрами и имеющих определенное количественное значение.
Алфавит системы счисления – это совокупность символов, используемых в данной системе счисления.
Основание системы счисления – количество цифр, используемых в данной системе счисления.
Разряд – номер позиции в числе. Нумеруются справа налево, начиная с нуля.
Вес разряда – число, равное основанию системы счисления в степени номера разряда.
В вычислительной технике в основном используются позиционные системы счисления – двоичная (BIN), десятичная (DEC), шести ад цатеричная (HEX), восьмеричная (ОСТ).
Привычное десятичное представление целых чисел уникальным образом формирует каждое целое число как конечную последовательность цифр. Арифметические операции (сложение, вычитание, умножение и деление) – это стандартные арифметические алгоритмы.
Десятичное представление используется для рациональных или вещественных чисел, оно более не уникально: многие рациональные числа имеют две записи – стандартная десятичная дробь (например, 2,31) и периодическая (например, 2,309999999...).
Системы счисления подразделяются на позиционные, непозиционные и смешанные.
Смешанные системы счисления:
– фибоначчиева система счисления (основывается на числах Фибоначчи);
– факториальная система счисления (основаниями является последовательность факториалов);
– система счисления майя. Майя использовали двадцатеричную систему счисления. Для записи основными знаками были точки (единицы) и отрезки (пятерки).
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения этой цифры в числе. При этом система может накладывать ограничения на положение цифр, например чтобы они были расположены в порядке убывания.
Непозиционные системы счисления:
– биномиальная система счисления (представление, использующее биномиальные коэффициенты);
– еврейская система счисления. В качестве цифр используются 22 буквы еврейского алфавита. Каждая буква имеет свое числовое значение от 1 до 400. Нуль отсутствует. Наиболее часто можно встретить цифры, записанные таким образом в нумерации лет по иудейскому календарю;
– греческая система счисления;
– римская система счисления;
– система остаточных классов (СОК). Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках;
– система счисления Штерна-Броко – это способ записи положительных рациональных чисел, основанный на дереве Штерна-Броко.
Количество цифр (знаков), используемых для представления чисел, называют основанием системы счисления. С помощью цифр в любой системе счисления число записывается как некоторая последовательность цифр.
Наиболее совершенными являются позиционные системы счисления, т.е. системы записи чисел, в которых вклад каждой цифры в величину числа зависит от ее положения (позиции) в последовательности цифр, изображающей число.
Например, в числе 53 цифра 5 в разряде десятков дает числу вклад в 50 единиц (5 х 10).
Число 444 записано тремя одинаковыми цифрами, но каждая из них имеет свое значение: четыре сотни, четыре десятка и четыре единицы.
То есть его можно записать так:
444 = 4 х 100 + 4 х 10 + 4 х 1
Или
444 = 4 х 102 + 4 х 101 + 4 х 100.
Нетрудно заметить, что если обозначить цифры числа как а2, а1 и а0, то любое трехзначное число может быть представлено в виде
N = a2 x102 + a1 х 101 + a0 х 100.
Число 10, степени которого используются в этой формуле (и именно столько разных цифр есть в десятичной системе), называют основанием системы счисления, а степени десятки – весами разрядов.
Для записи чисел в позиционной системе счисления с основанием р нужно иметь алфавит из р цифр (табл. 3.1). Обычно для этого при р < 30 используют р первых арабских цифр, при р > 10 к десяти арабским цифрам добавляют латинские буквы.
Таблица 3.1.