Тема урока «Объем прямой призмы»
Задачи урока:
образовательные: проверить знания ранее изученного теоретического материала, создать условия для активной познавательной деятельности учащихся по приобретению новых знаний, обеспечить усвоение формулы объема прямой призмы.
развивающие: способствовать развитию умений и навыков решения задач с использованием данной формулы (решения задач ЕГЭ), развивать логическое мышление, память, пространственное воображение, познавательный интерес.
воспитательные: воспитывать у учащихся потребность в приобретении и углублении знаний, вырабатывать умение слушать и вести диалог.
План урока
I. Мотивация учебной деятельности «Настроимся на урок!».
II. Актуализация опорных знаний учащихся
III. Изучение нового материала
IV. Физкультминутка
V. Закрепление изученного материала в ходе выполнения упражнений
VI. Контроль знаний
VII. Подведение итогов. Рефлексия
Ход урока
I. Мотивация учебной деятельности «Настроимся на урок!».
Цель: формирование мотива, желания работать.
Приветствие.
Эпиграфом к сегодняшнему уроку мне бы хотелось взять высказывание Г. Галилея, но немного переделанное «Геометрия является одним из могущественных средств для воплощения в жизнь многих идей». («Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать. Г. Галилей»)
II. Актуализация опорных знаний учащихся
Цель: создание ситуации успеха путем проверки владения материала прошлых уроков
В ходе изучения стереометрии мы с вами сталкиваемся с изучением различных геометрических фигур. Какими? (параллелепипед, призма, пирамида, куб, цилиндр, конус, шар).
Мы научились решать задачи на нахождение площадей пространственных фигур и приступили к нахождению объемов некоторых многогранников. Каких? (объем прямоугольного параллелепипеда, объем прямой призмы, основанием которой является прямоугольный треугольник).
Перед учениками на партах лежат карточки, которые необходимо заполнить:
Заполните пропуски в предложениях.
- Равные тела имеют … объёмы.
- Если тело составлено из нескольких тел, то его объём равен … объёмов этих тел.
- Объем прямоугольного параллелепипеда равен … трех его измерений.
- Объем прямоугольного параллелепипеда равен произведению … на ….
Вопрос учителя: Внимательно посмотрите на свои модели, какие это призмы? (прямые). А какую еще важную характеристику при изготовлении подарочной упаковки мы должны обязательно учитывать? (объем). Мы с вами заговорили о таком многограннике, как призма. Сможем мы найти площадь призмы? (да). А вычислить ее объем? (только для призмы, в основании которой прямоугольный треугольник или если это параллелепипед). Сформулируйте тему урока. Чем будем заниматься на уроке?
Ученики открывают тетради и записывают тему урока «Объем прямой призмы»
III. Изучение нового материала
Цель: изучить теорему об объеме прямой призмы.
Докажем теорему. Объём прямой призмы равен произведению площади основания на высоту. Сначала докажем теорему для треугольной прямой призмы, а затем – для произвольной. (Доказательство теоремы ведется с помощью беседы).
Дано: прямая призма
Доказать: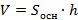 
Доказательство
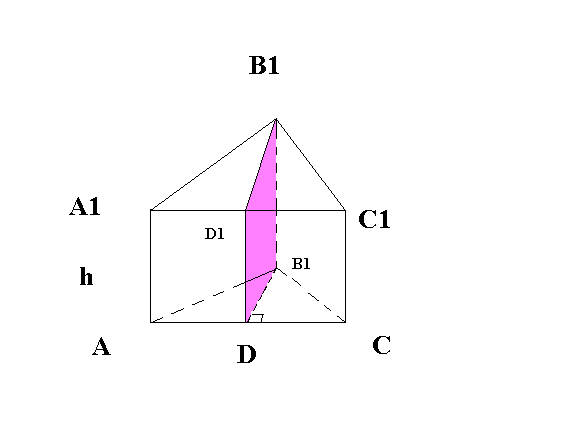
1) 
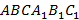- прямая призма. Проведем высоту 
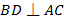, которая делит 
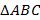на два треугольника 
. Плоскость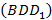 
разделяет данную призму на две призмы, основаниями которых являются прямоугольные треугольники . Поэтому объемы этих призм соответственно равны:
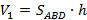
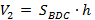
По свойству 2 (если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел)
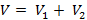
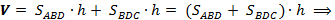
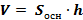
2) Докажем теорему для произвольной прямой призмы с высотой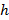 
и площадью основания S. Такую призму можно разбить на прямые треугольные призмы с высотой 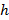. Выразим объем каждой треугольной призмы по формуле и сложим эти объемы. Вынося за скобки общий множитель 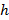, получим в скобках сумму площадей оснований треугольных призм, т. е. площадь S основания исходной призмы. Таким образом, объем исходной призмы равен 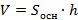. Теорема доказана.
IV. Физкультминутка
«Колечко» (упражнение для рук)
Поочередно перебирать пальцы рук, соединяя в кольцо большой палец и последовательно указательный, средний, безымянный и мизинец. Упражнения выполнять, начиная с указательного пальца и в обратном порядке от мизинца к указательному пальцу. Выполнять нужно каждой рукой отдельно, затем обеими руками вместе.
А теперь закрыли глаза, мысленно нарисовали окружность, в этой окружности изобразили улыбку. Что получилось? И вот с таким настроением продолжаем работать.