Элементы теории вероятностей
Представьте себе, что производится некоторый опыт или испытание, исход которого не может быть заранее предсказан. (Примеры: бросание монеты, вытаскивание наугад карты, сколько времени нужно жать нужного автобуса..). Все эти примеры относятся к области случайных явлений.
Определение. Явления, исход которых не может быть однозначно определен до того, как они произошли, называются случайными.
Пусть производится некоторый опыт, результат которого заранее неизвестен.
Определение. Случайное событие – всякий факт, который в результате опыта может произойти или не произойти.
Примеры.
1. Опыт - бросание монеты. Событие А – «выпадение герба».
2. Опыт – бросание 2-х монет. Событие В – «выпадение 2-х гербов».
3. Опыт – вынимание наугад 1 карты из колоды. Событие C – «попадание шестерки пик».
Теория вероятностей позволяет измерить количественно степень вероятности различных событий. Однако предсказывать можно только те случайные события, которые обладают высокой степенью правдоподобия.
Вопрос: Какое из событий в опыте подбрасывания игральной кости более вероятно: А – «выпадение шести очков» или B – «выпадение четного числа очков»?
Для оценки вероятности случайных событий необходимо выбрать единицу измерения. За такую единицу в теории вероятностей принято считать вероятность достоверного события. Достоверное событие – такое событие, которое в данном опыте непременно произойдет. Вероятность достоверного события будем считать единицей, а нулевую вероятность припишем невозможному событию, то есть такому, которое в данном опыте вовсе не может произойти (например выпадение числа очков больше шести).
|
|
Условимся обозначать вероятность случайного события P(А). Очевидно, что 
Классический способ вычисления вероятностей в схеме случаев
Пусть производится опыт, который имеет ряд возможных исходов: А1, А2, …, An
События А1, А2, …, An называются несовместными, если они взаимно исключают друг друга, т.е. никакие два из них не могут появиться вместе.
События А1, А2, …, An образуют полную группу, если они исчерпывают собой все возможные исходы, то есть не может быть так, чтобы в результате опыта ни одно из них не произошло.
События А1, А2, …, An называются равновозможными, если условия опыта обеспечивают одинаковую возможность (вероятность) появления каждого из них.
Если события А1, А2, …, An обладают всеми тремя свойствами, то есть а) несовместны б) образуют полную группу и в) равновозможные, то они называются случаями, а про опыт говорят, что он сводится к схеме случаев.
Примеры.
1. Опыт «бросание монеты». Сводится к схеме случаев. Почему?
2. Опыт «бросание «бросание игральной кости». Сводится к схеме случаев. Почему?
3. Опыт «бросание двух монет» Сводится к схеме случаев. Почему? Перечислите все случаи.
4.
Расчет вероятности для схемы случаев.
Если опыт сводится к схеме случаев, то вероятность любого события А в этом опыте может быть подсчитана как отношений числа случаев, благоприятных событию А, к общему числу случаев.
, где n – общее число случаев, mA – число случаев, благоприятных событию А.
Пример 0. Опыт состоит в бросании двух монет (трех монет, k монет). Найти вероятность того, что появится хотя бы один герб.
Пример 1. В урне находится 2 белых и 3 черных шара. Из урны наугад вынимается один шар. Требуется найти вероятность того, что этот шар будет белым.
|
|
Пример 2. В урне а белых и b черных шаров. Из урны вынимаются два шара. Найти вероятность того, что оба шара будут белыми.
Число сочетаний из к элементов по s:
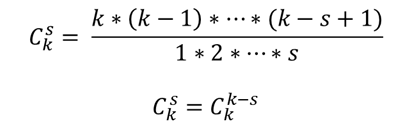
Пример 3. В партии из N изделий М бракованных. Из партии выбирается наугад k изделий. Определить вероятность того, что среди этих k изделий будет ровно m бракованных.
Решение. Общее число случаев m = 
. Найдем mD — число случаев, благоприятных событию D = {ровно m дефектных изделий в контрольной партии}.
Найдем число способов, какими из М дефектных изделий можно выбрать m для контрольной партии; оно равно 
Но ото еще не все: к каждой комбинации дефектных изделий нужно присоединить комбинацию из k — m доброкачественных; это можно сделать 
способами. Каждая комбинация из m дефектных изделий может сочетаться с каждой комбинацией из k — m доброкачественных; число тех и других комбинаций надо перемножить.
Поэтому число благоприятных событию D случаев равно
;
Вероятность и частота
Частотой события в серии из N опытов называется отношение числа опытов, в которых это событие произошло, к общему числу произведённых опытов. Частоту события ещё называют статистической вероятностью
Пусть производится некоторый опыт (эксперимент, испытание) со случайным исходом. Рассмотрим множество Q всех возможных исходов опыта; каждый его элемент qÎQ будем называть элементарным событием, а все множество Q — пространством элементарных событий.