Изучение явления термо-ЭДС при контакте металлов
Цель работы: изучение статистики Ферми-Дирака применительно к описанию электронов в металлах.
Приборы и материалы: установка……………..
Теория
Любое твердое тело представляет собой систему или коллектив, состоящий из огромного числа микрочастиц. Коллектив как целое, является системой, качест-венно отличной от отдельных частиц, и его поведение подчиняется иным законо-мерностям по сравнению с поведением отдельных частиц. Такими закономернос-тями являются статистические закономерности.
По характеру поведения в коллективе все частицы можно разделить на две группы: фермионы и бозоны. К фермионам относятся электроны, протоны, нейт-роны и другие частицы с полуцелым спином S ¤ 2, 3S ¤ 2.К бозонам относятся фотоны, фононы и другие частицы, обладающие целочисленным спином 0, ћ, 2ћ... В коллективе фермионы подчиняются принципу Паули: если данное квантовое состояние уже занято фермионом, то никакой другой фермион данного типа не может находиться в этом состоянии. Спин следует считать внутренним свойством (квантовомеханическим моментом) частицы, подобно заряду или массе. (Напри-мер состояние электрона в атоме характеризуется набором квантовых чисел n, l, m, s).
В классической механике состояние материальной точки (классической частицы) определяется заданием значений координат, импульса, энергии и т. д. Перечисленные величины называются динамическими переменными. Строго говоря, микрообъекту не могут быть приписаны указанные динамические пере-менные. Однако информацию о микрочастицах мы получаем, наблюдая их взаимодействие с приборами, представляющими собой макроскопические тела. Поэтому результаты измерений поневоле выражаются в терминах, разработан-ных для характеристики макротел, т. е. через значения динамических перемен-ных. В соответствии с этим измеренные значения динамических переменных приписываются микрочастицам. Например, говорят о состоянии электрона, в котором он имеет такое-то значение энергии, и т. д.
Если число состояний G оказывается одного порядка с числом частиц N, т.е если выполняется условие G / N » 1, такой коллектив частиц называется вырожденным.
(Если какой-либо энергетический уровень соответствует не одному, а нескольким квантовым состояниям, то он называется вырожденным.)
Энергия Ферми. Восновном состоянии твердое тело должно обладать минимальной энергией. Поскольку электроны подчиняются принципу Паули, и в каждом квантовом состоянии может находиться не более одного электрона, заключаем, что при температуре 0 К должны быть заполнены без промежутков все квантовые состояния электронов, начиная от уровня с наименьшей энер-гией. Из-за конечного числа электронов имеется конечный (верхний) заполненный уровень с наибольшей энергией, а последующие более высокие уровни свободны. Следовательно, при 0 К существует резкая границамежду областью заполненных уровней и областью свободных уровней.
При отличной от 0 К температуреэта граница размывается, поскольку в результате теплового движения энергия у некоторых электронов оказывается больше граничной энергии при 0 К, а у некоторых – меньше. В результате станут заполненными некоторые уровни энергии, которые при 0 К были свободными, и станут свободными некоторые уровни энергии, которые при 0 К были запол-ненными. Таким образом, возникает переходная область от полностью запол-ненных уровней энергии к полностью свободным. Ширина этой области имеет порядок kТ, где k = 1,38 ×10-23 Дж/К - постоянная Больцмана.
Распределение электронов по энергиям характеризуется функцией Ферми-Дирака: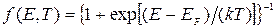 
(1)
где Е - энергия электрона; ЕF – энергия Ферми, зависящая от температуры.
Из (1) видно, что энергия Ферми - энергия, при которой функция Ферми-Дирака равна 1/2..
Функция Ферми-Дирака показывает, сколько в среднем приходится электро-нов на одно квантовое состояние с энергией Е. В случае вырожденных состояний энергией Е обладают несколько или даже очень много квантовых состояний. Функция Ферми-Дирака описывает среднее число электронов, приходящееся на каждое из этих состояний, а среднее число электронов, обладающих энергией Е, равно значению функции f (E,Т), умноженному на число квантовых состояний, принадлежащих вырожденному уровню энергии Е.
При Е < ЕF, Т→ 0 К имеем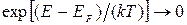 
и, следовательно,
f(E, T → 0 К) → 1, т. е. в каждом квантовом состоянии с энергией меньше EF при Т= 0 К находится по одной частице. При Е > ЕF, Т → 0 К имеем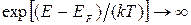 
и, следовательно, f(E, T → 0 К) → 0, т. е. квантовые состояния с энергией Е > ЕF свободны (в этих состояниях нет ни одного электрона). Распределение Ферми-Дирака показано на рис. 1и рис. 2. При комнат-ных температурах kT ~ 10-3 эВ и переходная область в распределении Ферми-Дирака очень мала. Поэтому при рассмотрении многих вопросов распределения Ферми-Дирака при комнатных температурах можно считать практически совпадающим с распределением при 0 К.
Для металлов понятие энергии Ферми имеет очень наглядный смысл: энергия Ферми является максимальной энергией электрона в зоне проводимости при Т = 0 К.
Это утверждение является точным при Т=0 К и достаточно точным для тем-ператур, когда размывание распределения Ферми-Дирака мало (для большинства металлов это утверждение справедливо вплоть до температур плавления и выше).
Для диэлектриков энергия Ферми приходится на запрещенную зону между валентной зоной и зоной проводимости. Электрон не может обладать такой энергией, т. е. энергия Ферми не соответствует энергии какого-либо реального электрона в диэлектрике. Аналогичное утверждение справедливо и для энергии Ферми в полупроводнике.
Однако это обстоятельство ни в каком смысле не уменьшает значения энергии Ферми для описания статистических свойств электронов в диэлектриках и полупроводниках в соответствии с формулой (1).
В состоянии равновесия энергии Ферми в металлах по разные стороны перехода металл-металл становятся равными друг другу.
Переходы и контакты. Весьма интересные и важные явления возникают в области перехода между частями твердого тела с различными электрическими свойствами. Например, два различных металла можно соединить сваркой в единое тело. Область, в которой эти металлы соединены, называется переходом металл-металл. При соприкосновении поверхностей – двух различных метал-лов образуется область соприкосновения, которая называется контактом. Явления в контактах и переходах совершенно различны и их не следует путать. Для твердотельной электроники наиболее важное значение имеют переходы.
Возникновение разности потенциалов на переходе металл–металл.
Энергия Ферми равна работе выхода А, взятой с отрицательным знаком:
EF = -А. (2)
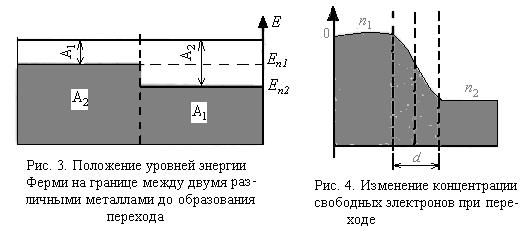
Как энергия Ферми, так и все другие энергии электрона в связанных со-стояниях внутри металла отрицательны. Относительные положения энергети-ческих спектров двух различных изолированных металлов, до того как они соединены и образовали переход, показаны на рис. 3. Видно, что работа выхода уменьшается с увеличением энергии Ферми.
Для понимания явлений в переходе металл – металл необходимо принять во внимание, что энергия Ферми зависит от концентрации свободных электронов в зоне проводимости – чем больше концентрация, тем больше энергия Ферми. Это означает, что при образовании перехода на границе металл – металл концент-рация газа свободных электронов по разные стороны границы различна. Она больше со стороны металла 1 с большей энергией Ферми (рис. 3).
Такое состояние не может быть равновесным, и электроны начнут диффун-дировать со стороны металла с большей концентрацией свободных электронов в сторону металла с меньшей концентрацией. В результате этого концентрация электронов в некоторой области вблизи границы со стороны металла с большей энергией Ферми уменьшается, и эта область заряжается положительно (работа выхода из этого металла увеличивается), а с другой стороны границы концентрация электронов увеличивается и эта область заряжается отрицательно (работа выхода из этого металла уменьшается). Благодаря возникновению зарядов по разные стороны границы образуется электрическое поле, напряженность которого направлена со стороны металла с большей энергией Ферми в сторону металла с меньшей энергией Ферми. Сила, действующая со стороны этого поля на электроны, направлена против диффундирующего потока электронов и создает упорядоченное движение электронов в противоположном диффузии направлении, т. е. электрический ток. Когда диффузионный поток электронов и электрический ток электронов уравновесят друг друга, наступает стационарное состояние. Изменение концентрации электронов от п1 до п 2 происходит в некоторой области d вблизи границы между металлами, которая и называется переходом (рис. 4).
В состоянии равновесия энергии Ферми в обоих металлах становятся равными. Уравнивание энергий Ферми является важнейшим фактором, определяющим характер процессов в переходе.
Это утверждение является почти очевидным, если принять во внимание требования принципа детального равновесия. Электрические потенциалы по разные стороны перехода становятся различными, а в переходе возникает электрическое поле (рис. 3).
Расчет разности потенциалов. С достаточной точностью можно рассматривать свободные электроны в переходе как газ. Поскольку там достаточно много свободных уровней энергии, можно воспользоваться распределением Больц-мана. Обозначим разность потенциалов Δ U12 = φ 2 – φ 1 (на рис. 5 эта величина отрицательна), заряд электрона q = - е.
Запишем распределение Больцмана в виде:
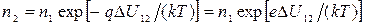(3)
Тогда 
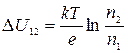(4)
Эта формула дает лишь грубую оценку разности потенциалов не только пото-му, что электронный газ более строго следует описывать с помощью распре-деления Ферми – Дирака, но и потому, что концентрация свободных электронов зависит от температуры.
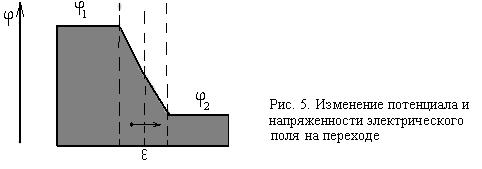
Однако для качественного рассмотрения явления формула (4) вполне пригодна. При комнатной температуре кТ/е ≈ 0,025 эВ. В обычных условиях в металлах концентрация свободных электронов имеет порядок 1028 электронов/м3. Из (4) можно заключить, что по порядку величины Δ U ~ 10-5 В/К, т. е. при комнатной температуре возникающая на переходе разность потенциалов имеет порядок тысячных долей вольта.
Термоэлектричество.
Возникающая на переходе разность потенциалов действует как сторонняя электродвижущая сила. Рассмотрим замкнутую цепь, состоящую из двух различных проводников, переходы между которыми поддерживаются при температурах Т1 и Т2 (рис. 6).
Разности потенциалов на переходах равны
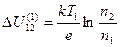
(5)
(индексы сверху обозначают номера переходов). Сторонняя электродвижущая сила в замкнутом контуре, равная сумме электродвижущих сил в переходах, на основании (5) может быть записана в виде
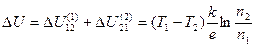(6)
где за положительное направление контура выбран обход по часовой стрелке.
Из (6) видно, что при Т2 ≠ T1 электродвижущая сила в замкнутом контуре Δ U ≠ 0. Следовательно, в контуре возникает электрический ток, называемый термо-электрическим. При Т2 = T1 сторонние термоэлектродвижущие силы на переходах в замкнутом контуре действуют на встречу друг другу и взаимно компенсируются. При Т1 ≠ T2 такой компенсации не происходит и в контуре действует электродвижущая сила Δ U [см. (6)].
Одним из самых распространенных применений термоэлектричества, являют-ся приборы для измерения температуры. Если в цепи (рис. 6) измерить силу тер-мотока и известны все характеристики цепи и переходов, то по температуре одного из переходов можно определить температуру другого. Приборы для измерения температур, основанные на таком принципе, называются термопара-ми. В других случаях это явление используется для генерации термоэлект-рического тока. Такие приборы называются термоэлементами. КПД таких приборов чрезвычайно низок. Однако термопары на полупроводниках обладают значительно большим КПД и в определенных целях используются для гене-рации электрического тока.
Эффект Зеебека.
В 1823 г. Т. Зеебек установил, что в цепи, состоящей из двух разнородных про-водников 1 и 2, возникает электродвижущая сила εr,, если контакты этих провод-ников А и В поддерживаются при различных температурах Т1 и Т2. Эта э. д. с. называется термоэлектродвижущей силой (термо-э. д. с). Как показывает опыт, в относительно узком интервале температур она пропорциональна разности темпе-ратур контактов А и В: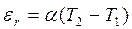 
.
Существует три источника возникновения термо-э. д. с: образование направ-ленного потока носителей в проводнике при наличии градиента температур, изменение положения уровня Ферми с температурой и увлечение электронов фононами.
Коэффициент пропорциональности называют дифференциальной или удельной термо-э. д. с. Он зависит от природы соприкасающихся проводников и температуры 
.
Величина контактной разности потенциалов зависит от многих факторов, но прежде всего от природы граничащих веществ. Очень важно, что контактные явления широко используются в технике, например, для измерения температур. ТермоЭДС
eT = a DT, (7)
a = (p2 k2 / e)[ m 02-1 - m 01-1] Тср, (8)
где Тср - средняя температура контактов,
DТ - разность температур контактов.
Величина ТЭДС зависит от разности температур и материалов термоэлемента, но не зависит ни от длины, ни от диаметра термоэлектродов. Термопарой или термоэлементом называется цепь из двух разнородных проводников, концы которых электрически соединены, например сваркой. Термопара может быть использована для измерения температуры после предварительной градуировки, т.е. экспериментального определения зависимости eT = f (T) при разных температурах рабочего конца и постоянной определенной температуре свободного конца. Плавная, приближающаяся к линейной, зависимости ТЭДС обеспечивает большое удобство градуировки термопары.
Термоэлектрические явления, возникающие при контакте различных металлов, описываются статистикой Ферми-Дирака. Эта функция распределения для вырожденного газа фермионов была впервые получена итальянским физиком Ферми и английским физиком Дираком:
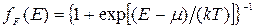(9)
где m - химический потенциал металла.
В данном случае m (мы имеем вырожденный газ фермионов) чаще называют уровнем Ферми.
Химический потенциал металла. Внутренняя энергия системы может изме-няться за счет совершения работы и обмена теплотой, а также при изменении числа частиц N в ней, так как каждая уходящая частица уносит с собой определен-ную энергию. Поэтому в общем виде закон сохранения энергии необходимо записать следующим образом:
где dN — изменение числа частиц в системе;
μ – химический потенциал системы;
Δ Q = T·dS – полученное или отданное системой количество теплоты;
Δ А = p·dV – работа, совершенная системой против внешних сил.
Химический потенциал системы имеет следующий физический смысл. Для изоли-рованной системы постоянного объема, которая не получает и не отдает теплоту
Отсюда находим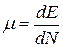 
.
Таким образом, химический потенциал выражает изменение энергии изолирован-ной системы постоянного объема, вызванное изменением в ней числа частиц на единицу.
Рассмотрим условие равновесия системы, полное число частиц которой остается неизменным, но частицы могут переходить из одного тела системы в другое. При-мером такой системы являются два электронных проводника, например два метал-ла, приведенные в контакт и поддерживаемые при постоянной температуре. Обозначим химический потенциал электронного газа в первом металле μ1 во втором μ2. Пусть из первого металла во второй перетекает dN электронов. Это вызовет уменьшение энергии первого металла на dE1 = μ1dN и увеличение энергии второго металла на dE2 = μ2dN. Для того чтобы металлы находились в равновесии, необходимо, чтобы
d E 1 = d E 2, или m 1d N = m 2d N
следовательно условие равновесия:
m 1 = m 2
Это условие справедливо не только для рассмотренного случая контакта двух электронных проводников, но и для контакта любых фаз: твердой и жидкой, жидкой и газообразной. Во всех случаях условием равновесия является равенство химических потенциалов.