АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ. Кривые 2-го порядка; их канонические уравнения и построение.
Кривые второго порядка.
Окружность, эллипс: канонические уравнения и построение.
Гипербола: канонические уравнения и построение.
Парабола: канонические уравнения и построение.
Полярные координаты.
Окружность, эллипс: канонические уравнения и построение.
Алгебраическим уравнением второго порядка называется уравнение вида:
Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0,
где хотя бы один из коэффициентов А, B, C отличен от нуля. Линии, задаваемые такими уравнениями, будем называть кривыми второго порядка. Рассмотрим некоторые из них.
Окружность
Под окружностью понимают геометрическое место точек, равноудаленных от некоторой фиксированной точки, называемой центром окружности.
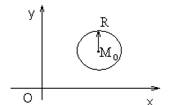
Рис. 1.8.1.
Пусть дана точка M 0(x 0, y 0) и некоторое число R (R ≥ 0).
Уравнение окружности радиуса R с центром в точке M 0 имеет вид:
| (x – x 0)2 + (y – y 0)2 = R 2 |
Если центр окружности M 0 находится в точке О (0,0), то уравнение окружности будет иметь вид:
| x 2 + y 2 = R 2 |
Пример. Установить вид кривых второго порядка, заданных уравнениями:
a) x 2 + y 2 + 6 x – 4 y – 3 = 0
б) x 2 + y 2 + 4 x – 2 y + 5 = 0
в) x 2 + y 2 – 2 x + 4 y + 7 = 0
Решение:
а) Перепишем данное уравнение, выделяя полный квадрат:
x 2 + 2·3 x + 9 – 9 + y 2 – 2·2 y + 4 – 4 – 3 = 0
(x + 3)2 + (y – 2)2 = 16
Данное уравнениеопределяет окружность радиуса 4 с центром
в точке M 0(–3, 2).
б) Преобразуем данное уравнение, также выделяя полный квадрат
x 2 + 2·2 x + 4 – 4 + y 2 – 2· y + 1 – 1 + 5 = 0
(x + 2)2 + (y – 1)2 = 0.
Полученное равенство возможно лишь при x = –2, y = 1. Данное уравнение определяет только одну точку M (–2, 1).
в) Преобразуем данное уравнение аналогично:
x 2 –2 x + 1 – 1 + y 2 + 2· y + 4 – 4 + 7 = 0
(x – 1)2 + (y + 2)2 = –2.
Это уравнение не имеет решения. Следовательно, не существует точек, удовлетворяющих данному уравнению.
Эллипс
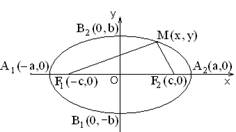
Рис.1.8.2.
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная.
Обозначим фокусы F 1 и F 2 расстояние между ними | F 1 F 2| = 2 c. Пусть | MF 1| + | MF 2| = 2 a. С помощью алгебраических преобразований можно получить уравнение эллипса:
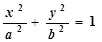
|
где b 2 = a 2 – c 2 > 0, так как a > c.
Уравнение называется каноническим уравнением эллипса. Точка О (0,0) является центром эллипса. Величины a и b (где а > 0 и b > 0) называются полуосями эллипса (отрезки 2 а и 2 b являются, соответственно, осями эллипса). Центр эллипса может находиться в произвольной точке M 0(x 0, y 0). Уравнение эллипса с центром в точке M 0(x 0, y 0) и осями, параллельными координатным осям, имеет вид:
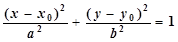
| (1.8.4) |
Пример. Показать, что уравнение 4 x 2 + 9 y 2 – 16 x – 18 y – 11 = 0 определяет эллипс. Сделать чертеж.
Решение: Преобразуем данное уравнение, выделяя полный квадрат: 4 x 2 + 9 y 2 – 16 x – 18 y – 11 = 0 Þ
4(x 2 – 2·2 x + 4 – 4) + 9(y 2 – 2 y + 1 – 1) – 11 = 0 Þ
4((x – 2)2·– 4) + 9((y – 1)2 – 1) – 11 = 0 Þ 4((x – 2)2·+9(y – 1)2 = 36.
Разделим обе части полученного уравнения на 36:
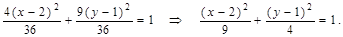
Получили уравнение эллипса вида (1.8.4) с центром в точке M 0(2,1) и полуосями а = 3, b = 2.
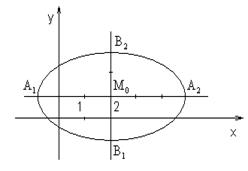
Для построения эллипса отметим в плоскости Oxy точку M 0(2, 1) и проведем через эту точку прямые, параллельные осям Ox и Oy. Отметим на горизонтальной прямой точки A 1 и A 2 отстоящие от M 0 на 3 единицы; на вертикальной прямой – точки B 1 и B 2 отстоящие от M 0 на 2 единицы. Точки A 1, B 2, A 2, B 1 соединим плавной линией. Эллипс построен.
Гипербола: канонические уравнения и построение.
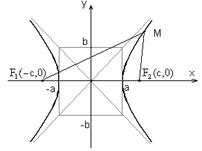
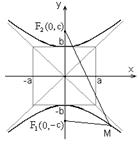
Гиперболой называется геометрическое место точек плоскости, разность расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная.
Обозначим фокусы F 1 и F 2, расстояние между ними | F 1 F 2| = 2 c. Пусть || MF 1| – | MF 2|| = 2 a.
Тогда канонические уравнения гиперболы имеют вид:
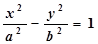
|
или
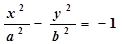
|
где b 2 = c 2 – a 2 > 0, так как a < c.
| 
|
Гиперболы, изображенные на рисунках, имеют центр
симметрии точку О (0,0) и две оси симметрии Ox и Oy. Величины a и b (где a > 0 и b > 0) называются полуосями гиперболы. При этом та ось симметрии, которую пересекает гипербола, называется действительной осью, а другая ось симметрии – мнимой. Если центр гиперболы находится в точке M 0(x 0, y 0), а оси параллельны координатным осям, то уравнение гиперболы имеет вид:
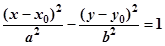
|
или
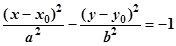
|
Пример. Показать, что уравнение 9 x 2 – 4 y 2 + 18 x + 8 y – 31 = 0 определяет гиперболу. Сделать рисунок.
Решение: Преобразуем данное уравнение, выделяя полный квадрат: 9 x 2 + 18 x – 4 y 2 + 8 y – 31 = 0 Þ
9(x 2 + 2 x) – 4(y 2 – 2 y) – 31 = 0 Þ
9(x 2 + 2 x + 1 – 1) – 4(y 2 – 2 y + 1 – 1) – 31 = 0 Þ
9((x + 1) 2 – 1) – 4(y – 1) 2 – 1) – 31 = 0 Þ
9(x + 1) 2– 4(y – 1) 2 = 36. Разделим обе части полученного уравнения на 36.
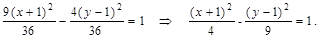
Получили уравнение гиперболы с центром в точке M 0(–1, 1) и а = 2, b = 3.
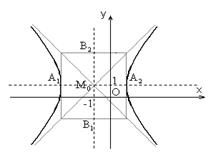
Для построения гиперболы отметим на плоскости Oxy точку M 0(–1, 1) и проведем через эту точку прямые, параллельные Ox и Oy. Отметим на горизонтальной прямой точки A 1 и A 2, отстоящие от M 0 на 2 единицы; на вертикальной прямой – точки B 1 и B 2, отстоящие от M 0 на 3 единицы. Построим прямоугольник, проходящий через указанные точки со сторонами, параллельными координатным осям. Проведем в этом прямоугольнике две диагонали. Искомая гипербола проходит через точки A 1 и A 2, асимптотически приближаясь к диагоналям прямоугольника.