Движение механизма относительно водила

То есть можно записать выражение, которое называется формулой Виллиса для планетарных механизмов
w*2 / w*1 = (w1-wh)/ (w2-wh) = -z1/z2 .
Вопрос №59
 При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при заданном числе силовых потоков (или числе сателлитов k) и заданном передаточном отношении u необходимо подобрать числа зубьев колес zi, которые обеспечат выполнение ряда условий. При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при заданном числе силовых потоков (или числе сателлитов k) и заданном передаточном отношении u необходимо подобрать числа зубьев колес zi, которые обеспечат выполнение ряда условий.
. Обеспечить возможность сборки механизма с подобранными числами зубьев колес при заданном числе сателлитов k > 1.
Для вывода формулы условия сборки воспользуемся следующим методом. Допустим, что все сателлиты устанавливаются на оси водила в одном и том же положении – точке В1. После установки первого сателлита, зубья колес z1 и z4 определенным образом установились относительно зубьев венцов сателлита. Тогда установить второй сателлит в этом же положении будет можно, если после поворота водила на угол jh колесо z1 повернется на целое число угловых шагов В. При этом зубья колес z1 и z4 установятся относительно зубьев венцов сателлита так же, как и при установке первого сателлита.
Угол поворота водила Þjh= 2 ×p / k;
Угловой шаг первого колеса Þt1 = 2 ×p / z1;
Угол на который повернется первое колесо при повороте водила на угол jh
j1 = jh× u1hÞj1 = 2 ×p× u1h / k;
Число угловых шагов t1 в угле j1 ÞB = j1 / t1 ,
где B - произвольное целое число.
Подставляем все эти выражения в формулу для B и после преобразований получаем
2 ×p× u1h× z1/ (k ×2 ×p) = B Þ u1h× z1 / k = B.
Поворачивать водило можно на угол jh плюс произвольное число р полных оборотов водила, то есть
jh= 2 ×p / k + 2 ×p×р = 2 ×p / k (1 + k × р).
С учетом этого, формула для условия сборки примет следующий вид
u1h× z1 / k (1 + k × р). = B.
| Вопрос №60
Кинематическое исследование типовых планетарных механизмов графическим и аналитическим методами.
Двухрядный механизм с одним внутренним и одним внешним зацеплением.
Дано: Кинематическая схема механизма – ri ,
числа зубьев колес - zi;
Определить: Передаточное отношение механизма -?
 Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис на звене 2 нарезаны два зубчатых венца:
z2, который зацепляется с зубчатым венцом z1 звена 1;
z3, который зацепляется с внутренним зубчатыми венцом z4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев
для внешнего зацепления колес z2 и z1 (w1-wh)/ (w2-wh) = - z2/z1;
для внутреннего зацепления колес z4 и z3 (w2-wh)/ (w3-wh) = z4/z3 .
Перемножим, правые и левые части этих уравнений, и получим
[(w1-wh)/ (w2-wh)]×[(w2-wh)/ (w3-wh)] = - z2× z4/(z1× z3),
[(w1-wh)/ (-wh)] = - z2× z4/(z1× z3),
u1h (3)= w1 / wh = 1 + z2×z4/(z1×z3).
Графическое определение передаточного отношения.
В системе координат ri0V построим треугольники распределения линейных скоростей звеньев. Для этого из точки А с ординатой r1 в выбранном произвольном масштабе mV, мм/м×с-1 отложим отрезок a a’. Через конец этого отрезка и начало координат проведем прямую, которая определит распределение скоростей для точек звена 1, лежащих на оси ri. Эта прямая образует с осью ri угол y1. Так как в точке с скорости звеньев 2 и 3 равны между собой и равны нулю, то соединяя точку с с прямой с точкой a’, получим линию распределения скоростей для звена 2. Так как точка принадлежит звеньям 2 и h, то ее скорость определяется по лучу с a’ для радиуса равного rB = (r1+r2), что в масштабе mV, мм/м×с-1 соответствует отрезку bb’. Соединяя точку b’ с началом координат прямой, найдем линию распределения скоростей для водила. Эта линия образует с осью ri угол yh. Передаточное отношение планетарного механизма определенное по данным графическим построениям можно записать так u1h(3)= w1/wh = tg y1 / tg yh = aa’/aa’’.
Вопрос №61
Подбор чисел зубьев по методу сомножителей.
Внутренним называют передаточное отношение механизма при остановленном водиле, то есть механизма с неподвижными осями или рядного механизма.
u14h = (z2×z4)/(z1×z3) =[ u1h / (0.95 … 1.05) – 1] = (B × D)/(A × C).
Разложим внутреннее передаточное отношение u14 h на сомножители - некоторые целые числа A, B, C и D. При этом сомножитель A соответствует числу зубьев z1, B - z2, C - z3 и D - z4 . Сомножители могут быть произвольными целыми числами, комбинация (B × D)/(A × C) которых равна u14 h. Для рассматриваемой схемы желательно придерживаться следующих диапазонов изменения отношений между сомножителями
B / A = z2 / z1 = 1 … 6 - внешнее зацепление ;
D / C = z4 / z3 = 1.1 … 8 – внутреннее зацепление .
Включим в рассмотрение условие соосности z1 + z2 = z4 - z3
и выразим его через сомножители a×(A + B) = b×(D – C).
Если принять, что коэффициенты a и b равны a = (D – C), b = (A + B),
то выражение превращается в тождество. Из этого тождества можно записать
z1= (D – C) × A × q; z3= (A + B) × C × q;
z2= (D – C) × B × q; z4= (A + B) × D × q;
где q - произвольный множитель.
Примеры подбора чисел зубьев для типовых планетарных механизмов.
Двухрядный планетарный редуктор с одним внешним и с одним внутренним зацеплением.
Дано: Схема планетарного механизма; u1h = 13; k = 3; Определить: zi -?
Внутреннее передаточное отношение механизма
u14 h = (z2×z4)/(z1×z3) =[ u1h/ (0.95 … 1.05) – 1] = 12 = (B×D)/(A×C) = 3×4/ (1×1) = 2×6/ (1×1)= 4×3/ (1×1) =...
Для первого сочетания сомножителей
z1= (D – C) × A × q = (4 – 1) × 1 × q = 3× q; z1= 18 > 17;
z2= (D – C) × B × q = (4 – 1) × 3 × q = 9× q; q = 6; z2= 54 > 17;
z3= (A + B) × C × q = (3 + 1) × 1 × q = 4× q; z3= 24 > 20;
z4= (A + B) × D × q = (3 + 1) × 4 × q = 16× q; z4= 96 > 85;
Проверка условия соседства sin(p/k) >max [(z2,3 + 2)/ (z1 + z2) ];
sin (p/3) > (54 + 2)/(18+54); 0.866 > 0.77 - условие выполняется.
Проверка условия сборки (u1h× z1 / k) × (1 + k × р) = B;
(13×18/3) ×(1 + 3 р) = В – целое при любом р.
Условие сборки тоже выполняется. То есть, получен первый вариант решения.
Габаритный размер R = (18 + 2× 54) = 126.
Для второго сочетания сомножителей
z1= (D – C) × A × q = (6 – 1) × 1 × q = 5× q; z1= 45 > 17;
z2= (D – C) × B × q = (6 – 1) × 2 × q = 10× q; q = 9; z2= 90 > 17;
z3= (A + B) × C × q = (2 + 1) × 1 × q = 3× q; z3= 27 > 20;
z4= (A + B) × D × q = (2 + 1) × 6 × q = 18× q; z4= 162 > 85;
Проверка условия соседства sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ];
sin (p/3) > (90 + 2)/(45+90); 0.866 > 0.681 - условие выполняется.
Проверка условия сборки (u1h× z1 / k) × (1 + k × р) = B;
(12×45/3) ×(1 + 3 р) = В – целое при любом р.
Условие сборки тоже выполняется и получен второй вариант решения.
Габаритный размер R = (45 + 2× 90) = 225.
Для третьего сочетания сомножителей
z1= (D – C) × A × q = (3 – 1) × 1 × q = 2× q; z1= 18 > 17;
z2= (D – C) × B × q = (3 – 1) × 4 × q = 8× q; q = 9; z2= 72 > 17;
z3= (A + B) × C × q = (1 + 4) × 1 × q = 5× q; z3= 45 > 20;
z4= (A + B) × D × q = (1 + 4) × 3 × q = 15× q; z4= 135 > 85;
Проверка условия соседства sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ];
sin (p/3) > (70 + 2)/(18+72); 0.866 > 0.8 - условие выполняется.
Проверка условия сборки (u1h× z1 / k) × (1 + k × р) = B;
(13×18/3) ×(1 + 3 р) = В – целое при любом р.
Условие сборки тоже выполняется и получен третий вариант решения.
Габаритный размер R = (18 + 2× 72) = 162.
Из рассмотренных трех вариантов габаритный наименьший размер получен в первом.
Вопрос №62
Условия подбора чисел зубьев.
Условия, которые необходимо выполнить при подборе чисел зубьев колес типового планетарного механизма:
1. заданное передаточное отношение с требуемой точностью;
u1h = [ 1+- (z2×z4)/(z1×z3) ] × (0.95 … 1.05).
2. соосность входного и выходного валов механизма;
mI (z1 +- z2) = mII × (z4 +- z3).z1 + z2 = z4 - z3
3. свободное размещение (соседство) сателлитов;
sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ].
4. сборку механизма при выбранных числах зубьев колес;
u1h× z1 / k (1 + k × р). = B.
5. отсутствие подреза зубьев с внешним зацеплением;
zi > zmin.(z с внеш>18)
6. отсутствие заклинивания во внутреннем зацеплении;
z с внеш. зуб. > 20; z с внутр. зуб. > 85;
zd = z с внутр. зуб - z с внеш. зуб. > 8.
7. минимальные относительные габариты механизма.
R = min [ max (z1 + 2×z2 ), (kK× z4) ],
kK - коэффициент, учитывающий особенности конструкции зубчатого колеса с внутренними зубьями.
Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис на звене 2 нарезаны два зубчатых венца:
z2, который зацепляется с зубчатым венцом z1 звена 1;
z3, который зацепляется с внутренним зубчатыми венцом z4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев
для внешнего зацепления колес z2 и z1 (w1-wh)/ (w2-wh) = - z2/z1;
для внутреннего зацепления колес z4 и z3 (w2-wh)/ (w3-wh) = z4/z3 .
Перемножим, правые и левые части этих уравнений, и получим
[(w1-wh)/ (w2-wh)]×[(w2-wh)/ (w3-wh)] = - z2× z4/(z1× z3),
[(w1-wh)/ (-wh)] = - z2× z4/(z1× z3),
u1h (3)= w1 / wh = 1 + z2×z4/(z1×z3).
Графическое определение передаточного отношения.
В системе координат ri0V построим треугольники распределения линейных скоростей звеньев. Для этого из точки А с ординатой r1 в выбранном произвольном масштабе mV, мм/м×с-1 отложим отрезок a a’. Через конец этого отрезка и начало координат проведем прямую, которая определит распределение скоростей для точек звена 1, лежащих на оси ri. Эта прямая образует с осью ri угол y1. Так как в точке с скорости звеньев 2 и 3 равны между собой и равны нулю, то соединяя точку с с прямой с точкой a’, получим линию распределения скоростей для звена 2. Так как точка принадлежит звеньям 2 и h, то ее скорость определяется по лучу с a’ для радиуса равного rB = (r1+r2), что в масштабе mV, мм/м×с-1 соответствует отрезку bb’. Соединяя точку b’ с началом координат прямой, найдем линию распределения скоростей для водила. Эта линия образует с осью ri угол yh. Передаточное отношение планетарного механизма определенное по данным графическим построениям можно записать так u1h(3)= w1/wh = tg y1 / tg yh = aa’/aa’’.
Вопрос №61
Подбор чисел зубьев по методу сомножителей.
Внутренним называют передаточное отношение механизма при остановленном водиле, то есть механизма с неподвижными осями или рядного механизма.
u14h = (z2×z4)/(z1×z3) =[ u1h / (0.95 … 1.05) – 1] = (B × D)/(A × C).
Разложим внутреннее передаточное отношение u14 h на сомножители - некоторые целые числа A, B, C и D. При этом сомножитель A соответствует числу зубьев z1, B - z2, C - z3 и D - z4 . Сомножители могут быть произвольными целыми числами, комбинация (B × D)/(A × C) которых равна u14 h. Для рассматриваемой схемы желательно придерживаться следующих диапазонов изменения отношений между сомножителями
B / A = z2 / z1 = 1 … 6 - внешнее зацепление ;
D / C = z4 / z3 = 1.1 … 8 – внутреннее зацепление .
Включим в рассмотрение условие соосности z1 + z2 = z4 - z3
и выразим его через сомножители a×(A + B) = b×(D – C).
Если принять, что коэффициенты a и b равны a = (D – C), b = (A + B),
то выражение превращается в тождество. Из этого тождества можно записать
z1= (D – C) × A × q; z3= (A + B) × C × q;
z2= (D – C) × B × q; z4= (A + B) × D × q;
где q - произвольный множитель.
Примеры подбора чисел зубьев для типовых планетарных механизмов.
Двухрядный планетарный редуктор с одним внешним и с одним внутренним зацеплением.
Дано: Схема планетарного механизма; u1h = 13; k = 3; Определить: zi -?
Внутреннее передаточное отношение механизма
u14 h = (z2×z4)/(z1×z3) =[ u1h/ (0.95 … 1.05) – 1] = 12 = (B×D)/(A×C) = 3×4/ (1×1) = 2×6/ (1×1)= 4×3/ (1×1) =...
Для первого сочетания сомножителей
z1= (D – C) × A × q = (4 – 1) × 1 × q = 3× q; z1= 18 > 17;
z2= (D – C) × B × q = (4 – 1) × 3 × q = 9× q; q = 6; z2= 54 > 17;
z3= (A + B) × C × q = (3 + 1) × 1 × q = 4× q; z3= 24 > 20;
z4= (A + B) × D × q = (3 + 1) × 4 × q = 16× q; z4= 96 > 85;
Проверка условия соседства sin(p/k) >max [(z2,3 + 2)/ (z1 + z2) ];
sin (p/3) > (54 + 2)/(18+54); 0.866 > 0.77 - условие выполняется.
Проверка условия сборки (u1h× z1 / k) × (1 + k × р) = B;
(13×18/3) ×(1 + 3 р) = В – целое при любом р.
Условие сборки тоже выполняется. То есть, получен первый вариант решения.
Габаритный размер R = (18 + 2× 54) = 126.
Для второго сочетания сомножителей
z1= (D – C) × A × q = (6 – 1) × 1 × q = 5× q; z1= 45 > 17;
z2= (D – C) × B × q = (6 – 1) × 2 × q = 10× q; q = 9; z2= 90 > 17;
z3= (A + B) × C × q = (2 + 1) × 1 × q = 3× q; z3= 27 > 20;
z4= (A + B) × D × q = (2 + 1) × 6 × q = 18× q; z4= 162 > 85;
Проверка условия соседства sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ];
sin (p/3) > (90 + 2)/(45+90); 0.866 > 0.681 - условие выполняется.
Проверка условия сборки (u1h× z1 / k) × (1 + k × р) = B;
(12×45/3) ×(1 + 3 р) = В – целое при любом р.
Условие сборки тоже выполняется и получен второй вариант решения.
Габаритный размер R = (45 + 2× 90) = 225.
Для третьего сочетания сомножителей
z1= (D – C) × A × q = (3 – 1) × 1 × q = 2× q; z1= 18 > 17;
z2= (D – C) × B × q = (3 – 1) × 4 × q = 8× q; q = 9; z2= 72 > 17;
z3= (A + B) × C × q = (1 + 4) × 1 × q = 5× q; z3= 45 > 20;
z4= (A + B) × D × q = (1 + 4) × 3 × q = 15× q; z4= 135 > 85;
Проверка условия соседства sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ];
sin (p/3) > (70 + 2)/(18+72); 0.866 > 0.8 - условие выполняется.
Проверка условия сборки (u1h× z1 / k) × (1 + k × р) = B;
(13×18/3) ×(1 + 3 р) = В – целое при любом р.
Условие сборки тоже выполняется и получен третий вариант решения.
Габаритный размер R = (18 + 2× 72) = 162.
Из рассмотренных трех вариантов габаритный наименьший размер получен в первом.
Вопрос №62
Условия подбора чисел зубьев.
Условия, которые необходимо выполнить при подборе чисел зубьев колес типового планетарного механизма:
1. заданное передаточное отношение с требуемой точностью;
u1h = [ 1+- (z2×z4)/(z1×z3) ] × (0.95 … 1.05).
2. соосность входного и выходного валов механизма;
mI (z1 +- z2) = mII × (z4 +- z3).z1 + z2 = z4 - z3
3. свободное размещение (соседство) сателлитов;
sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ].
4. сборку механизма при выбранных числах зубьев колес;
u1h× z1 / k (1 + k × р). = B.
5. отсутствие подреза зубьев с внешним зацеплением;
zi > zmin.(z с внеш>18)
6. отсутствие заклинивания во внутреннем зацеплении;
z с внеш. зуб. > 20; z с внутр. зуб. > 85;
zd = z с внутр. зуб - z с внеш. зуб. > 8.
7. минимальные относительные габариты механизма.
R = min [ max (z1 + 2×z2 ), (kK× z4) ],
kK - коэффициент, учитывающий особенности конструкции зубчатого колеса с внутренними зубьями.
|  Вопрос №63
При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при заданном числе силовых потоков (или числе сателлитов k) и заданном передаточном отношении u необходимо подобрать числа зубьев колес zi, которые обеспечат выполнение ряда условий.
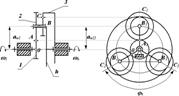
Обеспечение условия соседства сателлитов (при числе сателлитов k > 1).
Сателлиты размещаются на окружности радиуса aw. Вершины зубьев сателлитов не будут мешать движению друг друга, если выполняется условие
max (da2,3 ) < lB2B3.
Для зубчатых колес без смещения максимальный из диаметров сателлитов равен
=1 =0 =0 Вопрос №63
При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при заданном числе силовых потоков (или числе сателлитов k) и заданном передаточном отношении u необходимо подобрать числа зубьев колес zi, которые обеспечат выполнение ряда условий.
Обеспечение условия соседства сателлитов (при числе сателлитов k > 1).
Сателлиты размещаются на окружности радиуса aw. Вершины зубьев сателлитов не будут мешать движению друг друга, если выполняется условие
max (da2,3 ) < lB2B3.
Для зубчатых колес без смещения максимальный из диаметров сателлитов равен
=1 =0 =0
max (da2,3 ) = max [(z2,3 + 2× ha* +2× x2,3 - 2Dy) × m ] = max[(z2,3 + 2) × m ].
Расстояние между осями сателлитов
lB2B3 = 2 ×aw×sin(jh/2) = 2 × (r1 + r2) ×sin (p/k). = (z1 + z2) × m × sin (p/k).
Подставим полученные выражения в неравенство и получим условие соседства
max [(z2,3 + 2) × m ] < (z1 + z2) × m × sin (p/k),
sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ].
. Обеспечить возможность сборки механизма с подобранными числами зубьев колес при заданном числе сателлитов k > 1.
Для вывода формулы условия сборки воспользуемся следующим методом. Допустим, что все сателлиты устанавливаются на оси водила в одном и том же положении – точке В1. После установки первого сателлита, зубья колес z1 и z4 определенным образом установились относительно зубьев венцов сателлита. Тогда установить второй сателлит в этом же положении будет можно, если после поворота водила на угол jh колесо z1 повернется на целое число угловых шагов В. При этом зубья колес z1 и z4 установятся относительно зубьев венцов сателлита так же, как и при установке первого сателлита.
Угол поворота водила Þjh= 2 ×p / k;
Угловой шаг первого колеса Þt1 = 2 ×p / z1;
Угол на который повернется первое колесо при повороте водила на угол jh
j1 = jh× u1hÞj1 = 2 ×p× u1h / k;
Число угловых шагов t1 в угле j1 ÞB = j1 / t1 ,
где B - произвольное целое число.
Подставляем все эти выражения в формулу для B и после преобразований получаем
2 ×p× u1h× z1/ (k ×2 ×p) = B Þ u1h× z1 / k = B.
Поворачивать водило можно на угол jh плюс произвольное число р полных оборотов водила, то есть
jh= 2 ×p / k + 2 ×p×р = 2 ×p / k (1 + k × р).
С учетом этого, формула для условия сборки примет следующий вид u1h× z1 / k (1 + k × р). = B.
Вопрос №64
Кулачковые механизмы.
Кулачковым называется трехзвенный механизм с высшей кинематической парой входное звено которого называется кулачком, а выходное - толкателем (или коромыслом). Часто для замены в высшей паре трения скольжения трением качения и уменьшения износа, как кулачка, так и толкателя, в схему механизма включают дополнительное звено – ролик и вращательную кинематическую пару. Подвижность в этой кинематической паре не изменяет передаточных функций механизма и является местной подвижностью.
|
Поиск по сайту:
|

 При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при заданном числе силовых потоков (или числе сателлитов k) и заданном передаточном отношении u необходимо подобрать числа зубьев колес zi, которые обеспечат выполнение ряда условий.
При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при заданном числе силовых потоков (или числе сателлитов k) и заданном передаточном отношении u необходимо подобрать числа зубьев колес zi, которые обеспечат выполнение ряда условий. Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис на звене 2 нарезаны два зубчатых венца:
z2, который зацепляется с зубчатым венцом z1 звена 1;
z3, который зацепляется с внутренним зубчатыми венцом z4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев
для внешнего зацепления колес z2 и z1 (w1-wh)/ (w2-wh) = - z2/z1;
для внутреннего зацепления колес z4 и z3 (w2-wh)/ (w3-wh) = z4/z3 .
Перемножим, правые и левые части этих уравнений, и получим
[(w1-wh)/ (w2-wh)]×[(w2-wh)/ (w3-wh)] = - z2× z4/(z1× z3),
[(w1-wh)/ (-wh)] = - z2× z4/(z1× z3),
u1h (3)= w1 / wh = 1 + z2×z4/(z1×z3).
Графическое определение передаточного отношения.
В системе координат ri0V построим треугольники распределения линейных скоростей звеньев. Для этого из точки А с ординатой r1 в выбранном произвольном масштабе mV, мм/м×с-1 отложим отрезок a a’. Через конец этого отрезка и начало координат проведем прямую, которая определит распределение скоростей для точек звена 1, лежащих на оси ri. Эта прямая образует с осью ri угол y1. Так как в точке с скорости звеньев 2 и 3 равны между собой и равны нулю, то соединяя точку с с прямой с точкой a’, получим линию распределения скоростей для звена 2. Так как точка принадлежит звеньям 2 и h, то ее скорость определяется по лучу с a’ для радиуса равного rB = (r1+r2), что в масштабе mV, мм/м×с-1 соответствует отрезку bb’. Соединяя точку b’ с началом координат прямой, найдем линию распределения скоростей для водила. Эта линия образует с осью ri угол yh. Передаточное отношение планетарного механизма определенное по данным графическим построениям можно записать так u1h(3)= w1/wh = tg y1 / tg yh = aa’/aa’’.
Вопрос №61
Подбор чисел зубьев по методу сомножителей.
Внутренним называют передаточное отношение механизма при остановленном водиле, то есть механизма с неподвижными осями или рядного механизма.
u14h = (z2×z4)/(z1×z3) =[ u1h / (0.95 … 1.05) – 1] = (B × D)/(A × C).
Разложим внутреннее передаточное отношение u14 h на сомножители - некоторые целые числа A, B, C и D. При этом сомножитель A соответствует числу зубьев z1, B - z2, C - z3 и D - z4 . Сомножители могут быть произвольными целыми числами, комбинация (B × D)/(A × C) которых равна u14 h. Для рассматриваемой схемы желательно придерживаться следующих диапазонов изменения отношений между сомножителями
B / A = z2 / z1 = 1 … 6 - внешнее зацепление ;
D / C = z4 / z3 = 1.1 … 8 – внутреннее зацепление .
Включим в рассмотрение условие соосности z1 + z2 = z4 - z3
и выразим его через сомножители a×(A + B) = b×(D – C).
Если принять, что коэффициенты a и b равны a = (D – C), b = (A + B),
то выражение превращается в тождество. Из этого тождества можно записать
z1= (D – C) × A × q; z3= (A + B) × C × q;
z2= (D – C) × B × q; z4= (A + B) × D × q;
где q - произвольный множитель.
Примеры подбора чисел зубьев для типовых планетарных механизмов.
Двухрядный планетарный редуктор с одним внешним и с одним внутренним зацеплением.
Дано: Схема планетарного механизма; u1h = 13; k = 3; Определить: zi -?
Внутреннее передаточное отношение механизма
u14 h = (z2×z4)/(z1×z3) =[ u1h/ (0.95 … 1.05) – 1] = 12 = (B×D)/(A×C) = 3×4/ (1×1) = 2×6/ (1×1)= 4×3/ (1×1) =...
Для первого сочетания сомножителей
z1= (D – C) × A × q = (4 – 1) × 1 × q = 3× q; z1= 18 > 17;
z2= (D – C) × B × q = (4 – 1) × 3 × q = 9× q; q = 6; z2= 54 > 17;
z3= (A + B) × C × q = (3 + 1) × 1 × q = 4× q; z3= 24 > 20;
z4= (A + B) × D × q = (3 + 1) × 4 × q = 16× q; z4= 96 > 85;
Проверка условия соседства sin(p/k) >max [(z2,3 + 2)/ (z1 + z2) ];
sin (p/3) > (54 + 2)/(18+54); 0.866 > 0.77 - условие выполняется.
Проверка условия сборки (u1h× z1 / k) × (1 + k × р) = B;
(13×18/3) ×(1 + 3 р) = В – целое при любом р.
Условие сборки тоже выполняется. То есть, получен первый вариант решения.
Габаритный размер R = (18 + 2× 54) = 126.
Для второго сочетания сомножителей
z1= (D – C) × A × q = (6 – 1) × 1 × q = 5× q; z1= 45 > 17;
z2= (D – C) × B × q = (6 – 1) × 2 × q = 10× q; q = 9; z2= 90 > 17;
z3= (A + B) × C × q = (2 + 1) × 1 × q = 3× q; z3= 27 > 20;
z4= (A + B) × D × q = (2 + 1) × 6 × q = 18× q; z4= 162 > 85;
Проверка условия соседства sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ];
sin (p/3) > (90 + 2)/(45+90); 0.866 > 0.681 - условие выполняется.
Проверка условия сборки (u1h× z1 / k) × (1 + k × р) = B;
(12×45/3) ×(1 + 3 р) = В – целое при любом р.
Условие сборки тоже выполняется и получен второй вариант решения.
Габаритный размер R = (45 + 2× 90) = 225.
Для третьего сочетания сомножителей
z1= (D – C) × A × q = (3 – 1) × 1 × q = 2× q; z1= 18 > 17;
z2= (D – C) × B × q = (3 – 1) × 4 × q = 8× q; q = 9; z2= 72 > 17;
z3= (A + B) × C × q = (1 + 4) × 1 × q = 5× q; z3= 45 > 20;
z4= (A + B) × D × q = (1 + 4) × 3 × q = 15× q; z4= 135 > 85;
Проверка условия соседства sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ];
sin (p/3) > (70 + 2)/(18+72); 0.866 > 0.8 - условие выполняется.
Проверка условия сборки (u1h× z1 / k) × (1 + k × р) = B;
(13×18/3) ×(1 + 3 р) = В – целое при любом р.
Условие сборки тоже выполняется и получен третий вариант решения.
Габаритный размер R = (18 + 2× 72) = 162.
Из рассмотренных трех вариантов габаритный наименьший размер получен в первом.
Вопрос №62
Условия подбора чисел зубьев.
Условия, которые необходимо выполнить при подборе чисел зубьев колес типового планетарного механизма:
1. заданное передаточное отношение с требуемой точностью;
u1h = [ 1+- (z2×z4)/(z1×z3) ] × (0.95 … 1.05).
2. соосность входного и выходного валов механизма;
mI (z1 +- z2) = mII × (z4 +- z3).z1 + z2 = z4 - z3
3. свободное размещение (соседство) сателлитов;
sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ].
4. сборку механизма при выбранных числах зубьев колес;
u1h× z1 / k (1 + k × р). = B.
5. отсутствие подреза зубьев с внешним зацеплением;
zi > zmin.(z с внеш>18)
6. отсутствие заклинивания во внутреннем зацеплении;
z с внеш. зуб. > 20; z с внутр. зуб. > 85;
zd = z с внутр. зуб - z с внеш. зуб. > 8.
7. минимальные относительные габариты механизма.
R = min [ max (z1 + 2×z2 ), (kK× z4) ],
kK - коэффициент, учитывающий особенности конструкции зубчатого колеса с внутренними зубьями.
Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис на звене 2 нарезаны два зубчатых венца:
z2, который зацепляется с зубчатым венцом z1 звена 1;
z3, который зацепляется с внутренним зубчатыми венцом z4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев
для внешнего зацепления колес z2 и z1 (w1-wh)/ (w2-wh) = - z2/z1;
для внутреннего зацепления колес z4 и z3 (w2-wh)/ (w3-wh) = z4/z3 .
Перемножим, правые и левые части этих уравнений, и получим
[(w1-wh)/ (w2-wh)]×[(w2-wh)/ (w3-wh)] = - z2× z4/(z1× z3),
[(w1-wh)/ (-wh)] = - z2× z4/(z1× z3),
u1h (3)= w1 / wh = 1 + z2×z4/(z1×z3).
Графическое определение передаточного отношения.
В системе координат ri0V построим треугольники распределения линейных скоростей звеньев. Для этого из точки А с ординатой r1 в выбранном произвольном масштабе mV, мм/м×с-1 отложим отрезок a a’. Через конец этого отрезка и начало координат проведем прямую, которая определит распределение скоростей для точек звена 1, лежащих на оси ri. Эта прямая образует с осью ri угол y1. Так как в точке с скорости звеньев 2 и 3 равны между собой и равны нулю, то соединяя точку с с прямой с точкой a’, получим линию распределения скоростей для звена 2. Так как точка принадлежит звеньям 2 и h, то ее скорость определяется по лучу с a’ для радиуса равного rB = (r1+r2), что в масштабе mV, мм/м×с-1 соответствует отрезку bb’. Соединяя точку b’ с началом координат прямой, найдем линию распределения скоростей для водила. Эта линия образует с осью ri угол yh. Передаточное отношение планетарного механизма определенное по данным графическим построениям можно записать так u1h(3)= w1/wh = tg y1 / tg yh = aa’/aa’’.
Вопрос №61
Подбор чисел зубьев по методу сомножителей.
Внутренним называют передаточное отношение механизма при остановленном водиле, то есть механизма с неподвижными осями или рядного механизма.
u14h = (z2×z4)/(z1×z3) =[ u1h / (0.95 … 1.05) – 1] = (B × D)/(A × C).
Разложим внутреннее передаточное отношение u14 h на сомножители - некоторые целые числа A, B, C и D. При этом сомножитель A соответствует числу зубьев z1, B - z2, C - z3 и D - z4 . Сомножители могут быть произвольными целыми числами, комбинация (B × D)/(A × C) которых равна u14 h. Для рассматриваемой схемы желательно придерживаться следующих диапазонов изменения отношений между сомножителями
B / A = z2 / z1 = 1 … 6 - внешнее зацепление ;
D / C = z4 / z3 = 1.1 … 8 – внутреннее зацепление .
Включим в рассмотрение условие соосности z1 + z2 = z4 - z3
и выразим его через сомножители a×(A + B) = b×(D – C).
Если принять, что коэффициенты a и b равны a = (D – C), b = (A + B),
то выражение превращается в тождество. Из этого тождества можно записать
z1= (D – C) × A × q; z3= (A + B) × C × q;
z2= (D – C) × B × q; z4= (A + B) × D × q;
где q - произвольный множитель.
Примеры подбора чисел зубьев для типовых планетарных механизмов.
Двухрядный планетарный редуктор с одним внешним и с одним внутренним зацеплением.
Дано: Схема планетарного механизма; u1h = 13; k = 3; Определить: zi -?
Внутреннее передаточное отношение механизма
u14 h = (z2×z4)/(z1×z3) =[ u1h/ (0.95 … 1.05) – 1] = 12 = (B×D)/(A×C) = 3×4/ (1×1) = 2×6/ (1×1)= 4×3/ (1×1) =...
Для первого сочетания сомножителей
z1= (D – C) × A × q = (4 – 1) × 1 × q = 3× q; z1= 18 > 17;
z2= (D – C) × B × q = (4 – 1) × 3 × q = 9× q; q = 6; z2= 54 > 17;
z3= (A + B) × C × q = (3 + 1) × 1 × q = 4× q; z3= 24 > 20;
z4= (A + B) × D × q = (3 + 1) × 4 × q = 16× q; z4= 96 > 85;
Проверка условия соседства sin(p/k) >max [(z2,3 + 2)/ (z1 + z2) ];
sin (p/3) > (54 + 2)/(18+54); 0.866 > 0.77 - условие выполняется.
Проверка условия сборки (u1h× z1 / k) × (1 + k × р) = B;
(13×18/3) ×(1 + 3 р) = В – целое при любом р.
Условие сборки тоже выполняется. То есть, получен первый вариант решения.
Габаритный размер R = (18 + 2× 54) = 126.
Для второго сочетания сомножителей
z1= (D – C) × A × q = (6 – 1) × 1 × q = 5× q; z1= 45 > 17;
z2= (D – C) × B × q = (6 – 1) × 2 × q = 10× q; q = 9; z2= 90 > 17;
z3= (A + B) × C × q = (2 + 1) × 1 × q = 3× q; z3= 27 > 20;
z4= (A + B) × D × q = (2 + 1) × 6 × q = 18× q; z4= 162 > 85;
Проверка условия соседства sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ];
sin (p/3) > (90 + 2)/(45+90); 0.866 > 0.681 - условие выполняется.
Проверка условия сборки (u1h× z1 / k) × (1 + k × р) = B;
(12×45/3) ×(1 + 3 р) = В – целое при любом р.
Условие сборки тоже выполняется и получен второй вариант решения.
Габаритный размер R = (45 + 2× 90) = 225.
Для третьего сочетания сомножителей
z1= (D – C) × A × q = (3 – 1) × 1 × q = 2× q; z1= 18 > 17;
z2= (D – C) × B × q = (3 – 1) × 4 × q = 8× q; q = 9; z2= 72 > 17;
z3= (A + B) × C × q = (1 + 4) × 1 × q = 5× q; z3= 45 > 20;
z4= (A + B) × D × q = (1 + 4) × 3 × q = 15× q; z4= 135 > 85;
Проверка условия соседства sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ];
sin (p/3) > (70 + 2)/(18+72); 0.866 > 0.8 - условие выполняется.
Проверка условия сборки (u1h× z1 / k) × (1 + k × р) = B;
(13×18/3) ×(1 + 3 р) = В – целое при любом р.
Условие сборки тоже выполняется и получен третий вариант решения.
Габаритный размер R = (18 + 2× 72) = 162.
Из рассмотренных трех вариантов габаритный наименьший размер получен в первом.
Вопрос №62
Условия подбора чисел зубьев.
Условия, которые необходимо выполнить при подборе чисел зубьев колес типового планетарного механизма:
1. заданное передаточное отношение с требуемой точностью;
u1h = [ 1+- (z2×z4)/(z1×z3) ] × (0.95 … 1.05).
2. соосность входного и выходного валов механизма;
mI (z1 +- z2) = mII × (z4 +- z3).z1 + z2 = z4 - z3
3. свободное размещение (соседство) сателлитов;
sin (p/k) > max [(z2,3 + 2)/ (z1 + z2) ].
4. сборку механизма при выбранных числах зубьев колес;
u1h× z1 / k (1 + k × р). = B.
5. отсутствие подреза зубьев с внешним зацеплением;
zi > zmin.(z с внеш>18)
6. отсутствие заклинивания во внутреннем зацеплении;
z с внеш. зуб. > 20; z с внутр. зуб. > 85;
zd = z с внутр. зуб - z с внеш. зуб. > 8.
7. минимальные относительные габариты механизма.
R = min [ max (z1 + 2×z2 ), (kK× z4) ],
kK - коэффициент, учитывающий особенности конструкции зубчатого колеса с внутренними зубьями.
 Вопрос №63
При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при заданном числе силовых потоков (или числе сателлитов k) и заданном передаточном отношении u необходимо подобрать числа зубьев колес zi, которые обеспечат выполнение ряда условий.
Обеспечение условия соседства сателлитов (при числе сателлитов k > 1).
Сателлиты размещаются на окружности радиуса aw. Вершины зубьев сателлитов не будут мешать движению друг друга, если выполняется условие
max (da2,3 ) < lB2B3.
Для зубчатых колес без смещения максимальный из диаметров сателлитов равен
=1 =0 =0
Вопрос №63
При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при заданном числе силовых потоков (или числе сателлитов k) и заданном передаточном отношении u необходимо подобрать числа зубьев колес zi, которые обеспечат выполнение ряда условий.
Обеспечение условия соседства сателлитов (при числе сателлитов k > 1).
Сателлиты размещаются на окружности радиуса aw. Вершины зубьев сателлитов не будут мешать движению друг друга, если выполняется условие
max (da2,3 ) < lB2B3.
Для зубчатых колес без смещения максимальный из диаметров сателлитов равен
=1 =0 =0

