КОНТРОЛЬНАЯ РАБОТА № 2
Введение в математический анализ.
Производная и ее приложения.
Найти пределы функций, не пользуясь правилом Лопиталя.
а)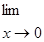 
;
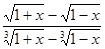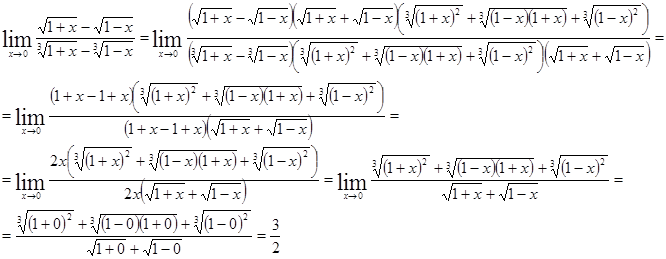
б)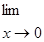 
;
в) 
;
г) 
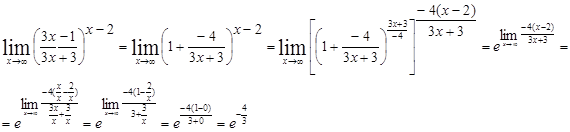
6.3.10. Задана функция у=f (х)и два значения аргумента x 1и х 2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
Данная функция определена и непрерывна на интервалах (-∞;-5),(-5;+∞).
Исследуем поведение функции в точках х1=-5, х2=-3. Найдём односторонние пределы.
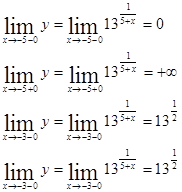
При х=-3 функция имеет одинаковые односторонние пределы и 
, значит, в этой точке функция непрерывна. При х=-5 функция имеет с одной стороны бесконечный предел, значит, в этой точках функция разрывна.
Сделаем схематический чертеж:
7.1.30. Найти производные 
данных функций.
a) 
;
б) 
при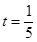 
;
в)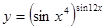 
.
Прологарифмируем обе части равенства:
Теперь продифференцируем обе части равенства:
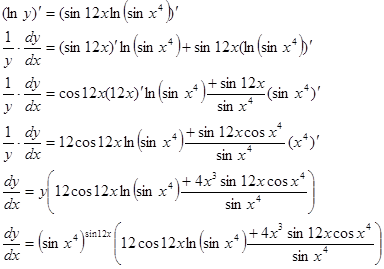
Найти пределы функции, применяя правило Лопиталя.
7.3.30. Методами дифференциального исчисления: а) исследовать функцию y = f (x) для 
и по результатам исследования построить ее график; б) Найти наименьшее и наибольшее значения заданной функции на отрезке [ a; b ].
а) 
б) [–2; 2].
1. Очевидно D (y) = (-¥;+¥).
2. 
. Функция является чётной.
3. Найдем точки пересечения с осями координат:
с осью Оу: x = 0, то у=-3;
с осью Ох: y = 0, то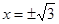 
.
4. Определим критические точки. Для этого найдем производную y'.
Тогда y' = 0 имеет решение х =0 –абсцисса точки экстремума. Определим знак первой производной на интервалах.
y'(x)
– +
Значит, на промежутке (0,+¥) функция возрастает, на промежутке (-¥,0) функция убывает.
5. Определим точки перегиба. Для этого найдем вторую производную y'' функции:
, тогда y'' = 0 имеет решение при 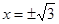- это абсциссы точек перегиба.
Определим знак второй производной на области определения.
y''(x)
– + –
Таким образом, при x Î(-¥, ), (, +¥) график функции выпуклый, при хÎ(, ) –вогнутый.
6. Функция определена и непрерывна на всей области определения. Выясним, имеет ли график функции наклонную асимптоту у=кх+в.
У=1 – горизонтальная асимптота.
По результатам исследования строим график функции:
б) Функция непрерывна на отрезке [-2;2]. Найдём производную
В данном случае критической является точка при х=0, причём точка принадлежит отрезку [-2;2]. Вычислим значение на концах отрезка:
Таким образом, наименьшее значение данной функции равно -0,333 и получаем его при х=0 в критической точке, наибольшее равное 0,077 получаем при х=-2 и х=2 на правой и левой границах.
КОНТРОЛЬНАЯ РАБОТА № 3
Неопределенный и определенный интегралы.
Функции нескольких переменных. Кратные интегралы.
Криволинейные и поверхностные интегралы.
Найти неопределенные интегралы. Результаты проверить дифференцированием.
а) 
Проверим результат дифференцированием:
б) 
;
Проверим результат дифференцированием:
в)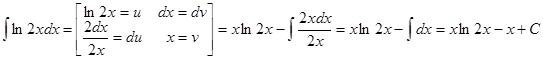 
;
Проверим результат дифференцированием:
г)
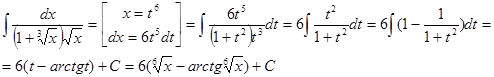
Проверим результат дифференцированием:
Исследовать интеграл на сходимость.
.
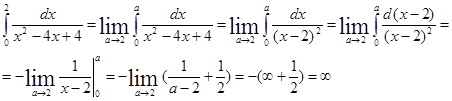Значит, интеграл расходится.
9.1.40. Дана функция двух переменных 
. Найти все частные производные первого и второго порядков. Обосновать равенство 
.
.
Равенство 
верно.
9.2.10. Дана функция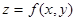 
и точка 
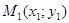. С помощью полного дифференциала вычислить приближенно значение функции в данной точке. Вычислить точное значение функции в точке 
и оценить относительную погрешность вычислений.
; 
.
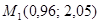Будем рассматривать z(М) как частное значение функции при x = 0,96 = x1, у =2,05 = у1. За x0 принимаем число 1, за у0 –число 2.
Тогда z (x 0,y0) = 
;
Переведём dx в радианы:
dx = x 1 – x 0 =0,96-1=-0,04,
dy = y 1 –y0 =2,05-2=0,05
Тогда получим:
» z (x 0,y0) + 
(x 0,y0) dx+ 
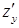(x 0,y0) dy =-3+(-2)(-0.04)-3*0.05=-3,07
Оценим погрешность: 
%
10.1.10. Вычислить криволинейный интеграл. Сделать чертеж дуги кривой L.
, где L – верхняя половина эллипса x = 3sin 2 t, y = 4cos 2 t. Интегрировать против часовой стрелки.
