Метод хорд (секущих).
Этот метод применяется при решении уравнений вида  , если корень уравнения отделён, т.е.
, если корень уравнения отделён, т.е.  и выполняются условия:
и выполняются условия:
1) 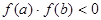 (функция
(функция  принимает значения разных знаков на концах отрезка
принимает значения разных знаков на концах отрезка  );
);
2) производная  сохраняет знак на отрезке
сохраняет знак на отрезке  (функция
(функция  либо возрастает, либо убывает на отрезке
либо возрастает, либо убывает на отрезке  ).
).
Первое приближение корня находится по формуле:  .
.
Для следующего приближения из отрезков 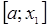 и
и  выбирается тот, на концах которого функция
выбирается тот, на концах которого функция  имеет значения разных знаков.
имеет значения разных знаков.
Тогда второе приближение вычисляется по формуле:
 , если
, если  или
или  , если
, если  .
.
Вычисления продолжаются до тех пор, пока не перестанут изменяться те десятичные знаки, которые нужно оставить в ответе.
Метод касательных (Ньютона).
Этот метод применяется, если уравнение  имеет корень
имеет корень 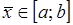 , и выполняются условия:
, и выполняются условия:
1)  (функция принимает значения разных знаков на концах отрезка
(функция принимает значения разных знаков на концах отрезка  );
);
2) производные  и
и 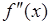 сохраняют знак на отрезке
сохраняют знак на отрезке  (т.е. функция
(т.е. функция  либо возрастает, либо убывает на отрезке
либо возрастает, либо убывает на отрезке  , сохраняя при этом направление выпуклости).
, сохраняя при этом направление выпуклости).
На отрезке  выбирается такое число
выбирается такое число  , при котором
, при котором 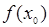 имеет тот же знак, что и
имеет тот же знак, что и 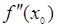 , т. е. выполняется условие
, т. е. выполняется условие  . Таким образом, выбирается точка с абсциссой
. Таким образом, выбирается точка с абсциссой  , в которой касательная к кривой
, в которой касательная к кривой  на отрезке
на отрезке  пересекает ось
пересекает ось  . За точку
. За точку  сначала удобно выбирать один из концов отрезка.
сначала удобно выбирать один из концов отрезка.
Первое приближение корня определяется по формуле:  .
.
Второе приближение корня определяется по формуле: 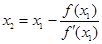 .
.
Вычисления ведутся до совпадения десятичных знаков, которые необходимы в ответе, или при заданной точности 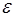 - до выполнения неравенства
- до выполнения неравенства  .
.
Достоинства метода: простота, быстрота сходимости.
Недостатки метода: вычисление производной и трудность выбора начального положения.
Комбинированный метод хорд и касательных.
Если выполняются условия:
1) 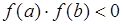 ,
,
2)  и
и 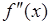 сохраняют знак на отрезке
сохраняют знак на отрезке  ,
,
то приближения корня  уравнения
уравнения  по методу хорд и по методу касательных подходят к значению этого корня с противоположных сторон. Поэтому для быстроты нахождения корня удобно применять оба метода одновременно. Т.к. один метод даёт значение корня с недостатком, а другой – с избытком, то достаточно легко получить заданную степень точности корня.
по методу хорд и по методу касательных подходят к значению этого корня с противоположных сторон. Поэтому для быстроты нахождения корня удобно применять оба метода одновременно. Т.к. один метод даёт значение корня с недостатком, а другой – с избытком, то достаточно легко получить заданную степень точности корня.
Схема решения уравнения методом хорд и касательных
1. Вычислить значения функции  и
и  .
.
2. Проверить выполнение условия  . Если условие не выполняется, то неправильно выбран отрезок
. Если условие не выполняется, то неправильно выбран отрезок  .
.
3. Найти производные  и
и 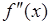 .
.
4. Проверить постоянство знака производных на отрезке  . Если нет постоянства знака, то неверно выбран отрезок
. Если нет постоянства знака, то неверно выбран отрезок  .
.
5. Для метода касательных выбирается за  тот из концов отрезка
тот из концов отрезка  , в котором выполняется условие
, в котором выполняется условие  , т.е.
, т.е. 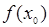 и
и  одного знака.
одного знака.
6. Приближения корней находятся:
а) по методу касательных:  ,
,
б) по методу хорд:  .
.
7. Вычисляется первое приближение корня:  .
.
8. Проверяется выполнение условия:  , где
, где 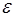 - заданная точность.
- заданная точность.
Если условие не выполняется, то нужно продолжить применение метода по схеме 1-8.
В этом случае отрезок изоляции корня сужается и имеет вид  . Приближённые значения корня находятся по формулам:
. Приближённые значения корня находятся по формулам:
 и
и  .
.
Вычисления продолжаются до тех пор, пока не будет найдено такое значение  , при котором
, при котором  и
и  совпадут с точностью
совпадут с точностью 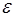 .
.
Пример. Решить уравнение 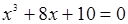 методом хорд и касательных с точностью 0,001, если известно, что корень уравнения
методом хорд и касательных с точностью 0,001, если известно, что корень уравнения  .
.
Решение.
1. Вычислим значения функции  на концах отрезка:
на концах отрезка:  ,
,  .
.
2. Проверим выполнение условия:  - условие выполняется.
- условие выполняется.
3. Найдём производные:  и
и 
 .
. 
4. На отрезке  производные
производные  и
и  , т.е. сохраняют знак, следовательно, условие выполняется.
, т.е. сохраняют знак, следовательно, условие выполняется.
5. Выберем значение  для метода касательных. Т.к.
для метода касательных. Т.к.  и
и  , то
, то  .
.
6. Найдём приближения корня:
а) по методу касательных: 
б) по методу хорд: 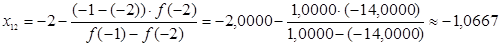 .
.
7. Найдём первое приближение корня:  .
.
8. Проверим выполнение условия:  - условие не выполняется, значит нужно продолжить вычисления.
- условие не выполняется, значит нужно продолжить вычисления.
9. Отрезок изоляции корня имеет вид:  .
.
10. Продолжим уточнение корня по схеме. Для этого найдём значения функции на концах суженного отрезка:
 ,
,  .
.
11. Проверим условие: 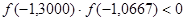 - выполняется, значит можно продолжить применение метода.
- выполняется, значит можно продолжить применение метода. 
12. Так как  и
и  на отрезке
на отрезке  , то для метода касательных:
, то для метода касательных: 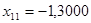 .
.
13. Вычислим значение производной:  .
.
14. Найдём новые значения концов отрезка изоляции:
 ,
,  .
.
15. Найдём второе приближение корня:  .
.
16. Проверим выполнение условия:  - неравенство неверное, значит необходимо продолжить вычисления.
- неравенство неверное, значит необходимо продолжить вычисления.
17. Отрезок изоляции корня имеет вид:  .
.
18. Вычислим значения функции:
 ,
,  .
.
19. Условие  - выполняется.
- выполняется.
20. Так как  и
и  на
на  , то для метода касательных
, то для метода касательных 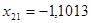 .
.
21. Вычислим производную: 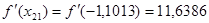 .
.
22. Вычислим:  ,
,
 .
.
23. Найдём третье приближение корня:  .
.
24. Проверим выполнение неравенства:  - условие выполняется, значит, цель достигнута.
- условие выполняется, значит, цель достигнута.
25. Следовательно,  или
или  - приближённое значение корня с точностью до 0,001.
- приближённое значение корня с точностью до 0,001.
Ответ:  .
.