В курсе кинематики было показано, что плоскопараллельное движение твердого тела эквивалентно движению плоской фигуры в ее плоскости. Последнее по методу полюса может быть разложено на переносное (поступательное движение вместе с кинематическими характеристиками точки, принятой за полюс), и относительное (вращение вокруг полюса). Первое из них определяется изменением во времени двух координат полюса, а второе – изменением во времени угла поворота. В задачах динамики в качестве полюса удобно выбирать центр масс тела С.
Для осуществления плоского движения свободного твердого тела необходимо выполнение следующих условий: масса тела должна быть распределена симметрично относительно плоскости движения, проходящей через центр масс; начальные скорости точек тела должны быть расположены в плоскостях, параллельных плоскости движения; главный вектор внешних сил должен лежать в этой плоскости, а главный момент – быть перпендикулярным к ней.
Для несвободного тела движение может быть плоским и в силу наложенных на него связей.
Задачи динамики плоского движения тела аналогичны задачам динамики материальной точки: либо по заданным силам требуется найти законы изменения во времени координат полюса и угла поворота, либо найти силы, вызывающие заданное плоское движение твердого тела.
Пусть система координат 
, имеющая начало в центре масс тела, движется поступательно относительно неподвижной координатной системы 
. Систему координат 
жестко свяжем с телом 
(рис. 3).
Рис. 3
Для описания поступательного движения тела применим теорему о движении центра масс; в проекциях на неподвижные оси получим
(12)
Дифференциальное уравнение вращения получим, применив теорему об изменении кинетического момента относительно оси 
, проходящей через центра масс С перпендикулярно плоскости движения. Тогда можно записать
(13)
Уравнения (12) и (13) называются дифференциальными уравнениями плоскопараллельного (или плоского) движения твердого тела.
Если тело совершает несвободное движение, то в число действующих сил необходимо включить реакции связей 
.
В таком случае уравнения плоского движения примут вид
(14)
Для получения решения задачи систему дифференциальных уравнений (14) следует дополнить уравнениями связей, наложенных на механическую систему.
Более подробно с материалом можно ознакомиться, например, в [1, 3, 4].
Пример решения задания
Механическая система, изображенная на рис. 4, состоит из груза 1, прикрепленного к земле демпфером, создающим силу сопротивления, пропорциональную скорости движения груза, двух соосных (насаженных неподвижно на единую ось) блоков и однородного диска. Составить математическую модель для определения движений всех тел механической системы, а так же реакций внешних и внутренних связей в виде замкнутой системы дифференциальных и алгебраических уравнений. Получить математическую модель для анализа условий равновесия рассматриваемой механической системы. Коэффициент сопротивления демпфера 
, вес груза 
, вес блоков 
, их радиусы 
и 
, а так же осевой момент инерции 
, вес диска 
и его радиус 
известны.
Рис. 4
Решение. Мысленно расчленим механическую систему на три тела (груз, соосные блоки и диск), приложив к каждому из тел соответствующие внешние силы (рис. 4). Для описания движения тел зададим соответствующие оси координат и запишем дифференциальные уравнения движения.
Уравнение для первого груза:
;
уравнения для соосных блоков:
;
;
;
уравнения для диска:
;
;
.
Сила сопротивления движению, создаваемая демпфером, пропорциональна скорости движения груза 
, а сопротивление качению диска учтено приложением момента трения качения 
.
Поскольку нити нерастяжимы, а качение диска происходит без проскальзывания, можно дополнить систему дифференциальных уравнений уравнениями кинематических связей:
или 
; или 
;
или 
; или 
;
или 
; или 
.
В итоге получена замкнутая система из двенадцати уравнений с двенадцатью неизвестными.
Рассматриваемая механическая система обладает одной степенью свободы, что позволяет кинематические характеристики выразить через соответствующие характеристики одного тела, например груза. Тогда для скоростей тел можно записать соотношения
.
Очевидно, что для ускорений должны быть записаны аналогичные соотношения.
Теперь умножим дифференциальные уравнения тел на соответствующие переходные коэффициенты (так уравнение вращения соосных блоков на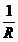 
, дифференциальное уравнение поступательного движения диска на 
, а дифференциальное уравнение вращения диска на 
) и сложим полученные выражения с учетом уравнений кинематических связей. После несложных преобразований получим дифференциальное уравнение, описывающее движение первого груза не содержащее реакций внутренних связей:
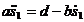, или 
,
где 
, 
Заметим, что при условии 
механическая система стремиться двигаться в предполагаемом направлении. Если это условие не выполняется, то рассматриваемая механическая система стремиться двигаться в противоположном направлении. В таком случае все слагаемые в выражении для 
, кроме момента трения качения, изменят свои знаки на противоположные, что изменит значение величины .
Решение этого неоднородного дифференциального уравнения может быть получено либо методом разделения переменных, либо угадыванием решения. Рассмотрим второй путь получения решения. Как известно, решение неоднородного дифференциального уравнения представимо суммой решения однородного дифференциального уравнения и частного решения неоднородного уравнения:
.
Будем предполагать, что решение однородного уравнения 
имеет вид 
. Тогда 
, а 
Подставим полученные выражение в однородное уравнение. Оно выполняется при 
, 
. Найденное решение однородного уравнения имеет вид 
.
Частное решение будем искать в виде 
, где 
– неизвестная постоянная.
Заметим, что рекомендация о поисках частного решения в виде правой части нами не могла быть выполнена, так как константа 
уже содержится в решении однородного дифференциального уравнения; отмеченная особенность потребовала искать линейно независимый вид решения, например, умножив константу на время 
.
Возьмем от выражения для частного решения первую и вторую производные и подставим их в исходное дифференциальное уравнение. Оно удовлетворяется при 
. Теперь общее решение примет вид 
.
Постоянные интегрирования и 
находятся из начальных условий. Так если в начальный момент времени груз получил скорость 
, то 
. Окончательно выражение для закона движения груза механической системы будет
.
Решение задачи выполнено в общем виде. Напомним, что движение тела (или механической системы) обусловлено действующими силами и начальными условиями. Если в начальный момент механическая система покоилась, то при условии
она стремится двигаться в предполагаемом направлении.
При условии
,
что означает, момент трения качения больше момента сил, действующих на диск, механическая система будет покоиться. Если эти условия не выполняются, то рассматриваемая механическая система стремится двигаться в противоположном направлении. В таком случае все слагаемые в выражении для , кроме момента трения качения, изменят свои знаки на противоположные, что изменит значение величины , т.е.
.
Если в начальный момент времени какому либо из тел механической системы придали скорость движения, то могут иметь место несколько случаев. Так, при выполнении первого условия и совпадении направления начальной скорости с предполагаемым направлением движения, механическая система будет двигаться в том же направлении с изменяющейся скоростью до тех пор, пока сила сопротивления от демпфера не уравновесит действие остальных сил; после этого скорость движения механической системы будет постоянной. Если направление начальной скорости не совпадает с предполагаемым направлением движения, то движение механической системы будет происходить в два этапа. На первом этапе движение механической системы будет происходить в заданном направлении до полной остановки с уменьшающейся скоростью (при этом в дифференциальном уравнении вместо следует использовать 
). Второй этап движения будет иметь нулевую начальную скорость и происходить так, как в случае совпадения направления начальной скорости с предполагаемым направлением движения механической системы.
При выполнении второго условия скорость движения механической системы будет уменьшаться до полной остановки вне зависимости от направления начальной скорости движения.
При выполнении условия
механическая система стремится двигаться в сторону, противоположную указанной на рис. 4. Если направление начальной скорости задано в ту же сторону – механическая система будет двигаться в том же направлении с изменяющейся скоростью до тех пор, пока сила сопротивления от демпфера не уравновесит действие остальных сил; после этого скорость движения механической системы будет постоянной. Если направление начальной скорости не совпадает с предполагаемым направлением движения, то движение механической системы будет происходить, как указывалось выше, в два этапа.
В случае необходимости определить законы движения других элементов механической системы следует воспользоваться уравнениями кинематических связей.
Если требуется рассчитать величины реакций внешних и внутренних связей, следует воспользоваться дифференциальными уравнениями движения тел, подставив в них выражения соответствующих ускорений и скоростей (либо алгебраическими уравнениями, если изменения соответствующей координаты не происходит).
При анализе условий равновесия механической системы в составленных дифференциальных уравнениях следует положить ускорения и скорости движения равными нулю, а перемещения (если они входят в выражения для действующих сил) – равными отклонениям в положении статического равновесия (последнее замечание актуально для механических систем с упругими связями).
Уравнение равновесия для первого груза:
;
уравнения для соосных блоков:
;
;
;
уравнения для диска:
;
;
.
При записи уравнений учтено, что в состоянии покоя сила сопротивления демпфера 
, а момент трения качения 
.
Полученная система алгебраических уравнений позволяет записать условия равновесия и вычислить реакции внешних и внутренних связей. Очевидно, что для рассмотренного случая равновесие будет иметь место при условии
.
Напомним, что учет трения скольжения и (или) трения качения для одного твердого тела приводил к определению диапазона значений параметров, при которых равновесие было возможно. Для механической системы можно сделать аналогичные выводы. Например: равновесие рассматриваемой механической системы возможно при 
, где
.
С решением подобных примеров можно ознакомиться, например, в [2, 3, 4].
Задание 4. Применение теоремы об изменении
кинетической энергии к изучению
движения механической системы