Запишем теорему об изменении кинетической энергии механической системы в дифференциальной форме:
(30)
– производная по времени от кинетической энергии механической системы равна мощности всех действующих сил (внешних и внутренних, либо активных (задаваемых) и реакций связей).
В дифференциальной форме, основанной на понятии работы силы за элементарный промежуток времени, получим
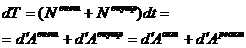(31)
Интегрируя (31) на интервале времени [0; 
], получим интегральную форму записи теоремы об изменении кинетической энергии
(32)
В частном случае, когда для совокупности внешних и внутренних сил системы можно записать выражение потенциальной энергии
,
вместо (31) имеем соотношение
(33)
В такой системе выполняется закон сохранения полной механической энергии
,
а сама система называется консервативной.
Заметим, что хотя теорема об изменении кинетической энергии позволяет составить для механической системы только одно уравнение, этого уравнения оказывается вполне достаточно для исследования движения многих систем с одной степенью свободы.
В случае, когда связи между телами механической системы не деформируются (например, нити не растягиваются и не провисают), мощность (работа) внутренних сил действия и противодействия равна нулю, а выражения (30), (31) и (32) приобретают более простой вид.
В случае наличия идеальных связей (мощность (работа) их реакций равна нулю), выражения (30), (31) и (32) так же приобретают более простой вид.
Более подробно с материалом можно ознакомиться, например, в [1, 3, 4].
Пример решения задания
Для механической системы, изображенной на рис. 4, получить дифференциальное уравнение движения груза.
Решение. Для решения задачи воспользуемся теоремой об изменении кинетической энергии в дифференциальной форме (30). Мысленно освободимся от связей, приложив к телам механической системы соответствующие реакции (рис. 4).
Составим выражение для кинетической энергии механической системы:
.
Запишем уравнения кинематических связей:
или 
;
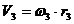или 
;
или 
.
При записи учтено, что мгновенный центр скоростей диска, катящегося без скольжения, расположен в точке его соприкосновения с плоскостью.
В формулу для кинетической энергии подставим угловые скорости вращения соосных блоков, диска и скорость центра масс диска, выраженные через скорость первого груза; тогда
.
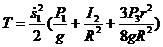При получении результата учтено, что осевой момент инерции однородного диска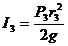 
.
Продифференцировав выражение для кинетической энергии по времени, получим левую часть равенства (29):
.
Отметим, что в рассматриваемой системе внутренние связи не деформируемы, поэтому мощность внутренних сил должна быть равна нулю. Точка приложения опорных реакций соосных блоков неподвижна, а точка приложения опорных реакций диска является его мгновенным центром скоростей; очевидно, что эти связи идеальны.
Запишем выражение для мощности действующих сил:
при записи учтено, что сила сопротивления демпфера 
, а момент трения качения 
.
В выражение для мощности подставим скорость центра диска, выраженную через скорость первого груза, и вынесем последнюю за общие скобки; тогда
.
Приравняем выражения для левой и правой частей равенства (29) и сократим их на 
. Перенесем переменные величины в левую часть равенства и поделим все слагаемые на постоянный коэффициент при ускорении первого груза. Окончательный вид искомого дифференциального уравнения будет
,
где 
.
Решение полученного неоднородного дифференциального уравнения было получено выше.
С решением подобных примеров можно ознакомиться, например, в [2, 3, 4].
Задание 5. Применение метода кинетостатики
для определения усилий в связях механической системы