Вопрос 1. Систематические коды

Обратное преобразование линейного кода

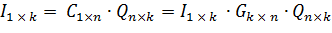, (1.1)

где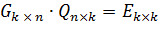

получают передаваемое сообщение I _{1 x k}.

 

Можно облегчить процесс декодирования и сделать С более наглядным.

При изучении свойств кодов, исправляющих ошибки, надо иметь в виду, что для любого канала с независимыми ошибками два кода, отличающиеся только расположением символов, имеют одну и ту же вероятность ошибки. Вообще между двумя такими кодами имеется очень тесная связь, и поэтому они называются эквивалентными. В результате любой элементарной опе­рации ^[1] над строками матрицы получается матрица с тем же самым пространством строк, и поэтому измененная матрица является по­рождающей матрицей для того же самого кода.

 

Если одна матрица может быть получена из другой путем комбинации элементарных операций над строками и перестановок столбцов, то эти две матри­цы называются комбинаторно-эквивалентными.

Любая порождающая матрица G комбинаторно-эквивалентна некоторой матрице G’, имеющей ступенчатую каноническую фор­му:

1. Первый ненулевой элемент каждой строки равен «1»;

2. Каждый столбец, содержащий первый ненулевой элемент некоторой строки, в качестве всех остальных элементов содержит нули;

3. первый ненулевой элемент каждой строки стоит правее первого ненулевого столбца каждой предыдущей строки.

4. Все нулевые строки расположены ниже всех ненулевых строк.

Пример: левый край матрицы приведенного ступенчатого вида по строкам не обязательно имеет вид единичной матрицы, поскольку константы в третьем столбце не являются ведущими элементами своих строк

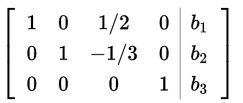
Перестановкой столбцов можно образовать приведено-ступенчатую матрицу: сгруппировать слева k столбцов, содержащих единицы в качестве первых ненулевых элементов каждой строки, так чтобы они образовали единичную матрицу размерности k x k, в результате чего получится комбинаторно-эк­вивалентная матрица G" вида

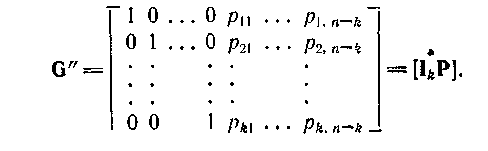
Таким об­разом, для каждой порождающей матрицы G существует комби­наторно-эквивалентная ей матрица G", имеющая приведенно-ступенчатую форму, и каждый код эквивалентен пространству строк некоторой матрицы, имеющей приведенно-ступенчатую форму.

Следует обратить внимание, что матрица G” порождает другой код, но эквивалентный исходному по помехоустойчивости.

Тогда пусть I_{1 x k} = (I₁,I₂,..., I_k) – произвольный набор длины k. Рассмотрим вектор С:

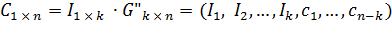
где

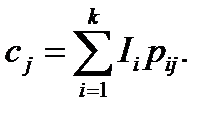
Таким образом, первые k компонент кодового вектора могут быть произвольно выбранными информационными символами, а каж­дая из последних n — k компонент является линейной комбина­цией первых k компонент.

Благодаря этому код становится систематическим (линейным разделимым) кодом, кодирование сильно упрощается, а раскодирование вообще не требует алгебраических операций.

Справка: в разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат исключительно для коррекции ошибок. Неразделимые коды не имеют четкого разделения кодовой комбинации на информационные и проверочные символы.

Разделимые блочные коды, в свою очередь, делятся на несистематические и систематические. Наиболее многочисленный класс разделимых кодов составляют систематические коды. Основная их особенность в том, что проверочные символы образуются как линейные комбинации информационных символов.

 

Существует теорема: Каждый линейный код эквивалентен систематиче­скому коду.

Существует простой способ нахождения проверочной матрицы кода, если задана порождающая матрица кода в приведенно-сту­пенчатой форме.

Теорема. (О проверочной матрице). Если V’— пространство строк матрицы G” = [E_kP], где E_k— единичная матрица размерности k x k, a Р— матрица размерности k x (n — k), то V’ является нулевым пространством матрицы Н” = [ – Р^Т E_n-k], где E_n-k — единичная матрица размер­ности (n - k) x (n - k).

Здесь уместно отметить, что «– P» это матрица, такая, что P + (–P) = 0. Для двоичного исчисления «–P» = P.

Пример. Порождающая матрица задана в приведенно-ступенчатой форме.

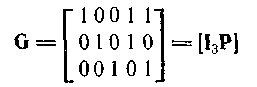
Если положить

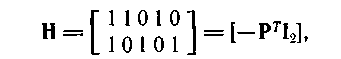
то GH^T=HG^T = 0, и пространство строк каждой матрицы яв­ляется нулевым пространством для другой матрицы.

Вопрос 2. Коды Хэмминга

Двоичный код Хэмминга (Ричард Уэсли Хэмминг –Richard Wesley Hamming), систематический код, имеет кодовое расстояние d = 3 и позволяет обнаруживать и исправлять одиночную ошибку.

Корректирующие коды обозначают (n,k), где n – количество символов в кодовой комбинации, из них k – количество информационных символов.

Коды Хэмминга для r проверочных символов

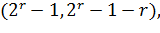r = 3, 4, 5, …

т.е. (7, 4), (15, 11), (31,26) и т.д.

Построение кодов Хэмминга основано на принципе проверки на четность числа единичных символов: каждый проверочный символ представляет собой сумму по модулю 2 некоторой подпоследовательности информационных символов.

Рассмотрим варианты кода Хэмминга для r = 3.

Вариант 1.

Пусть

Тогда для преобразования

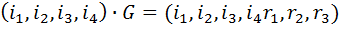
нужна матрица

,

а по теореме 2.1. (о проверочной матрице)

.

Само преобразование

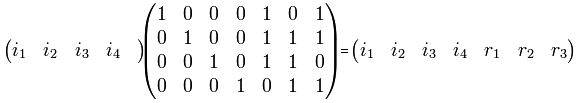
В декодере строится вектор-синдром (S ₁, S ₂, S ₃)

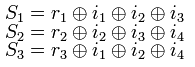
Если синдром равен «0» т.е. (0, 0, 0), то это означает, что ошибки нет.

Если синдром отличен от нуля, то по таблице синдромов можно найти позицию ошибки:

Рассмотрим еще один вариант, который иногда только и называется кодом Хэмминга (т.е. предыдущий вариант в этом смысле – не код Хэмминга).

Код сначала зададим при помощи его проверочной матрицы.

Рассмотрим матрицу Н из нулей и еди­ниц, содержащую m = 3 строки и 2^m — 1= 7 столбцов, причем столбцами являются все ненулевые двоичные наборы длины т, записанные так, что номер столбца записан в двоичной системе счисления в этом столбце

,

 

Число проверочных символов со­ставляет r = 3, число информационных символов равно 4, а общее количество бит в кодовой комбинации = 7.

Код по определению является разделимым (систематическим), т.е. в нем явным образом заданы информационные и проверочные символы.

Можно было бы задать например I₁I₂I₃I₄P₁P₂P₃, но так делать нецелесообразно.

Кодирование легко проводится, если в качестве проверочных вы­браны первый, второй и четвертый символы, так как в этом случае каждый из этих символов входит только в одно из проверочных соотношений, задаваемых матрицей Н. Т.е. используют следующую последовательность: P₁P₂I₁P₃I₂I₃I₄.

Чтобы рассчитать P₁P₂ и P₃, следует решить следующую систему уравнений, которая при данной последовательности распадается на отдельные уравнения.

 

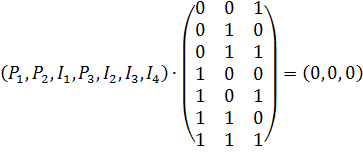
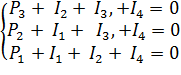
Откуда

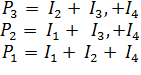
Если при принятой нами проверочной матрице H взять последовательность I₁I₂I₃I₄P₁P₂P₃, то система не распадется на три независимых уравнения.

Полученные уравнения для P₁P₂P₃ позволяют воссоздать порождающую код матрицу G

 

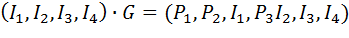
Рассмотрим обнаружение ошибок.

Предположим, что передавался кодовый вектор u и появилась одна ошибка. Тогда будет получен вектор u + е, где е — вектор, содержащий «1» в том разряде, где произошла ошибка, и «0» во всех остальных разрядах.

Синдром равен

 

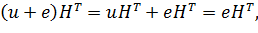
так как u — кодовый вектор и поэтому принадлежит нулевому пространству матрицы Н и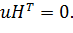

Но поскольку е — вектор, содержащий единственную единицу в разряде, соответствующем ошибке, то синдром еН^Т равен как раз той строке матрицы Н^Т, которая соот­ветствует ошибке.

Таким образом, сравнивая синдром с матрицей Н^Т, можно найти положение ошибки и затем исправить ее, просто заменив соответствующий символ на правильный.

Особенно удобно это делать, если использовать в качестве i-гo столбца матрицы Н двоичное представление числа i. Тогда для каждой отдельной оди­ночной ошибки синдром является двоичным представлением но­мера разряда, в котором произошла ошибка. Это расположение первоначально использовано Хэммингом.

Пример. Чтобы закодировать информационные символы 1100, нужно определить проверочные символы в слове P₁ P₂ 1 Р₃ 1 0 0. Кодовый вектор равен 0111100.

Предположим, что пятый символ принят ошибочно, тогда будет получен вектор 0111000. Легко вычислить синдром, который оказывается равным 101 — величине, соответ­ствующей пятому столбцу матрицы Н и указывающей на то, что ошибка произошла в пятом символе полученного вектора. Синдром является двоичным кодом числа 5, поскольку каждый столбец матрицы Н выбирался как двоичное представление номера столбца.

Существует понятие расширенный код Хэмминга. для q ≥ 2.