, (6)
где 
- постоянные, а 
- функция специального вида. Из теории известно, что общее решение (16) имеет вид
,
где 
- общее решение соответствующего однородного уравнения, а 
- частное решение неоднородного уравнения (6).
Укажем вид частного решения уравнения (16), если имеет вид
, (7)
где 
и 
- вещественные числа, 
и 
- многочлены соответственно степеней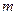 
и 
.
Составим контрольное число 
.
· Если число не является корнем характеристического уравнения, то
(8)
где 
и 
- многочлены степени 
с неизвестными коэффициентами.
· Если число 
есть корень характеристического уравнения кратности 
, то
. (9)
Пример 3. Определить и записать структуру частного решения линейного неоднородного дифференциального уравнения по виду функции 
.
. Это линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами вида (16). Найдем общее решение однородного уравнения:
, 
, 
, 
.
1) 
.
Правая часть неоднородного уравнения имеет вид (17).
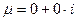=0. Числа 0 нет среди корней характеристического уравнения, следовательно, учитывая (8),
, 
многочлен второй степени, или 
.
2) 
.
=1. Число 1 содержится два раза среди корней характеристического уравнения. Тогда из (19)
, 
.
3) 
. Здесь 
. Число 
не содержится среди корней характеристического уравнения, следовательно:
4) 
. Число не содержится среди корней характеристического уравнения, поэтому:
, или 
(
константа).
Следовательно, частное решение представляет собой сумму
.
Пример 4. Найти методом неопределенных коэффициентов общее решение дифференциального уравнения 
.
Общее решение неоднородного уравнения имеет вид: 
,
где 
- общее решение соответствующего однородного уравнения, 
- частное решение неоднородного уравнения.
Найдем общее решение линейного однородного уравнения 
.
Составим характеристическое уравнение:
, 
, 
; 
,
.
Найдем частное решение по виду правой части 
.
Контрольное число 
. Числа 
нет среди корней характеристического уравнения, следовательно:
.
Подставим в исходное уравнение 
. В таблице 2 в первом столбце представлено частное решение и его производные с соответствующими коэффициентами, во втором столбце - выражение этих функций с учетом вида 
.
Таблица 2.
Вычисление левой части неоднородного дифференциального уравнения методом неопределенных коэффициентов
| 
|
| 
|
| 
|
Суммируем все строки таблицы и приравниваем к правой части (22). Затем приравниваем коэффициенты при одинаковых функциях:
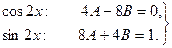
Отсюда 
; 
, 
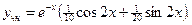
Общее решение
.
2.3. Метод Лагранжа, или метод вариации произвольных постоянных. Метод Лагранжа можно применять в случаях, когда правая часть уравнения (6) не имеет специального вида (7). В этом случае общее решение (6) ищется в виде
. (10)
Здесь 
и 
- неизвестные функции 
, удовлетворяющие системе уравнений
, (11)
и 
составляют фундаментальную систему решений соответствующего однородного уравнения.
Пример 5. Решить дифференциальное уравнение методом вариации произвольных постоянных (методом Лагранжа).
- неоднородное линейное уравнение 2-го порядка вида (6). Т.к. правую часть этого уравнения нельзя представить в виде (7), метод неопределенных коэффициентов здесь неприемлем. Применяем метод Лагранжа. Пусть 
, где 
и 
- неизвестные функции, 
- фундаментальная система решений. Найдем и 
.
, 
, 
, 
, 
.
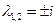Для нахождения функций и составим систему (11):
Решаем ее методом Крамера:
.
Решая последние два дифференциальных уравнения, получим:
;
;
- общее решение уравнения (9).