Дифференциальным уравнением первого порядка называется уравнение вида 
или 
, где 
- неизвестная функция от 
. Иногда дифференциальное уравнение 1-го порядка записывают в дифференциалах: 
.
Решением дифференциального уравнения называется такая дифференцируемая функция 
, которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество.
Общим решением дифференциального уравнения первого порядка в области 
называется функция 
, обладающая следующими свойствами:
1) она является решением данного уравнения при любых значениях произвольной постоянной 
;
2) для любого начального условия 
при 
, т.е.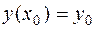 
, такого, что 
, существует единственное значение 
, при котором решение 
удовлетворяет заданному начальному условию.
Равенство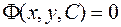 
, неявно задающее общее решение, называется общим интегралом дифференциального уравнения.
Частным решением дифференциального уравнения называется любая функция 
, которая получается из общего решения при конкретном значении . (
называется частным интегралом).
Задача, в которой требуется найти частное решение уравнения , удовлетворяющее начальному условию 
при 
(или 
) называется начальной задачей или задачей Коши.
Построенный на плоскости 
график любого решения 
дифференциального уравнения называется интегральной кривой.
1.1 Дифференциальное уравнение с разделяющимися переменными. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде
или в виде
(1)
уравнение (1) преобразуют следующим образом:
Предполагая, что 
и 
, разделим уравнение (2) на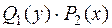 
. Получим уравнение, которое решается такое уравнение почленным интегрированием
.
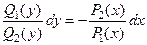
Пример 1. Найти общее решение дифференциального уравнения 
; построить несколько интегральных кривых; найти уравнение кривой, проходящей через точку с координатами (1,-3).
- это дифференциальное уравнение с разделяющимися переменными вида (1). Преобразуем его:
тогда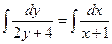 
;
, или 
.
Чтобы упростить данное выражение, запишем произвольную постоянную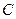 
в виде 
:
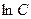(произвольная постоянная 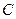не изменится при делении или умножении на любое число, отличное от нуля).
Чтобы найти уравнение кривой, проходящей через точку (1;-3), найдем 
по начальным условиям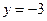 
при 
:
.
Уравнение кривой: 
. Это частное решение заданного уравнения.
1.2. Линейные дифференциальные уравнения первого порядка. Уравнение вида
(2)
где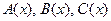 
- заданные функции и 
, или после деления на 
и некоторого преобразования записанное в виде
, (3)
называется линейным дифференциальным уравнением 1-го порядка. Решение линейного уравнения 1-го порядка может быть получено с помощью подстановки:
; 
, где 
- неизвестные дифференцируемые функции.
Пример 2. Уравнение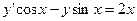 
- линейное уравнение первого порядка вида (2), где 
. Введем подстановку (9). Подставляя вместо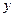 
и 
соответствующие выражения, получим
Приравнивая выражение в скобках к нулю, получим уравнение:
, которое является уравнением 1-го порядка с разделяющимися переменными. Решим его:
- общее решение.
, 
, 
, 
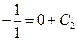, частное решение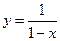 
.
.