Для разработки поискового алгоритма КЭНС необходимо задать область поиска. При этом учитывают возможный темп изменения различных ошибок и длительность функционирования поискового алгоритма. Время одного цикла функционирования поискового алгоритма КЭНС в практических реализациях составляет единицы минут.
В наиболее простом виде поисковый алгоритм КЭНС представляет собой различитель числовых последовательностей конечной длины на фоне помех с критерием оптимизации по минимуму целевой функции сравнения.
Одна из сравниваемых последовательностей заполняется измерениями высоты рельефа местности в темпе их поступления в процессе функционирования алгоритма КЭНС. Для определенности будем называть эту последовательность «измеренной». Остальные последовательности заполняются значениями высот рельефа местности из эталонной бортовой карты рельефа местности в точках, соответствующих заданным гипотезам об ошибках определения навигационных параметров грубой навигационной системой.
Область поиска КЭНС представляет собой подобласть в пространстве Rn, которая в большинстве случаев является n -мерным прямоугольным параллелепипедом, построенный вокруг точки текущих навигационных определений ГНС ЛА, n – размерность вектора состояния модели ошибок ГНС. Для построения гипотез в области поиска задается сетка разбиения, узловые точки которой характеризуются фиксированными значениями оцениваемых параметров.
Δ xi 1(0), Δ yi 2(0), Δ Нi 3(0), Δ Vxi 4(0), Δ Vyi 5(0), …;
где i 1 = 1, …, N 1;
i 2 = 1, …, N 2;
N 1 – число гипотез о значении ошибки по координате x;
N 2 – число гипотез о значении ошибки по координате y.
Общее число гипотез в области поиска определяется произведением
|
|
N = N 1× N 2× N 3…× N n, (1)
и влечет за собой соответствующие требования к вычислительным ресурсам для реализации алгоритма сравнения N гипотез. Последнее обстоятельство объясняет тот факт, что на практике поисковые алгоритмы КЭНС чаще всего применяются для моделей ошибок с минимальной размерностью вектора состояния.
В поисковом алгоритме КЭНС должны проверяться гипотезы о возможных значениях ошибок местоположения ЛА. Одна из гипотез состоит в том, что позиционные ошибки БИНС нулевые, т.е. δx = 0 и δy = 0, будем обозначать ее как Н 00. Другие гипотезы соответствуют предположениям о том, что ошибки БИНС ненулевые и кратны линейным интервалам дискретизации области поиска ∆ x и ∆ y. Интервалы ∆ х, ∆ у выбираются из соображений желаемой точности оценивания. Тогда полное множество гипотез может быть записано в виде:
Hmn = { δxm = m ∆ x, δyn = n ∆ y }, (2)
где - Nx ≤ m ≤ Nx; - Ny ≤ n ≤ Ny. 
Параметры Nx и Ny выбираются на основании априорной информации об ошибках БИНС к моменту запуска алгоритма КЭНС так, чтобы обеспечить накрытие сеткой разбиения всей предопределенной области возможных ошибок БИНС, т.е. чтобы выполнялось условие полноты набора гипотез:
Чаще всего линейные интервалы дискретизации ∆ x и ∆ y, а также константы алгоритма Nx и Ny выбирают одинаковыми по величине, поэтому при дальнейшем изложении материала без потери общности можно считать, что
Δ x = Δ y = Δ;
Nx = Ny = N.
Принцип функционирования поискового алгоритма КЭНС для задачи оценивания координатных ошибок иллюстрирует рисунок 1.
|
|
Рисунок 1 − Принцип функционирования поискового алгоритма КЭНС
Выходом БИНС в моменты времени tj, j = 1, 2, … S являются оценки текущих координат местоположения ЛА, преобразованные в прямоугольную систему координат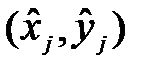 
.
Для каждой точки 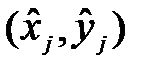определяются координаты точек, соответствующих гипотезам Hmn:
.
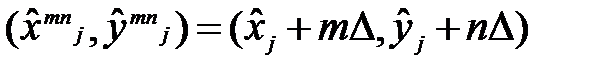В точках 
осуществляется восстановление эталонных значений высоты рельефа местности:
.
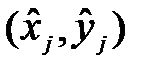Положение точек относительно представлено на рисунке 1 черными точками.
Целевая функция поискового алгоритма КЭНС является функцией двух целочисленных аргументов – индексов m, n, и зависит от числа измерений S как параметра. Для каждой пары индексов (m, n) она представляет собой сумму S квадратов разностей измеренных значений высоты рельефа местности и эталонных значений для гипотезы с индексами (m, n):
; (3)
где – Nx ≤ m ≤ Nx;
– Ny ≤ n ≤ Ny;
– эталонное значение высоты рельефа местности из бортовой карты;
– измеренное значение высоты рельефа местности, соответствующее формуле (18);
Δ – линейный интервал дискретизации области поиска.
Решением поисковой КЭНС является точка сетки разбиения, в которой целевая функция (3) принимает наименьшее значение:
. (4)