На рисунке 4 приведен модуль, моделирующий работу грубой коррекции местоположения с помощью КЭНС.
Входными параметрами данного модуля являются:
1) координаты местоположения ЛА, полученные от БИНС;
2) показания баровысотомера
3) показания радиовысотомера.
Также необходимо заранее задать шаг координатной сетки в подключаемой карты.
В блоке Differences calculation реализовано грубое определение смещения реального положения ЛА относительно измеренного с помощью БИНС. Для этого, вокруг грубых координат, полученных от БИНС строится область поиска (её размер выбирается исходя из баланса между высокой нагрузкой на ЭВМ и точностью работы системы). Внутри каждого узла области поиска записываются квадраты разностей высот – измеренной и эталонной (полученной из карты). При этом, в одном из узлов, формируется экстремум. Расстояние от этого максимума до центра области поиска (координат, полученных от БИНС) и есть реальное положение ЛА.

Рисунок 4 – Модуль, моделирующий работу грубой коррекции КЭНС в пакете Matlab-Simulink
Для формирования экстремума, необходимо, чтобы система отработала несколько циклов работы, при этом данные, записанные в области поиска накапливаются и экстремум становится более выраженным. Блок Chart является конечным автоматом с двумя состояниями, он оценивает получаемую от блока Differences calculation матрицу данных, и если координаты экстремума внутри матрицы значительно не смещаются в течение нескольких тактов работы системы, то автомат переходит во второе состояние и устанавливается флаг о готовности решения КЭНС, данные передаются в БИНС, накопленные значения сбрасываются. Если положение минимума изменяется, то система продолжает накапливать и оценивать получаемые данные. На рисунке 3 приведен принцип функционирования КЭНС.

Рисунок 4– Принцип работы КЭНС
2.3 Моделирование работы α - β фильтра
На рисунке 5 приведены входные и выходные данные, необходимые для работы данного фильтра. Входными параметрами являются – смещения координат от КЭНС, и текущее время работы системы. На выходе получаем скорректированные значения тех же смещений КЭНС, а также время проведения последней коррекции.

Рисунок 5 – Блок реализующий алгоритм работы α - β фильтра в пакете Matlab-Simulink
Ниже приведен алгоритм работы α - β фильтра, реализованного в виде функции Matlab.
function [corr, t_corr] = fcn(delta, t)%описание функции фильтра
persistent x alfa beta t_pred state;%объявление внутренних переменных
if isempty(x)
%первый такт работы фильтра, инициализация переменных,
%запись полученных от КЭНС данных
%фильтрация невозможно из-за недостатка данных
x = zeros(1,4);
x(1:2) = delta;
alfa = 0.75;
beta = 0.45;
t_pred = t;
state = 1;
else
%второй такт работы фильтра,
%оценивается скорость изменения данных за 2 такта
x_ = x;
dT = t - t_pred;
t_pred = t;
if state == 1
state = 2;
x(1:2) = delta;
x(3:4) = (x(1:2)-x_(1:2))/dT;
else
%третий такт работы фильтра, оценивается скорость изменения данных
%и полученные координаты от КЭНС, вносятся поправочные
%коэффициенты, рассчитанные ранее.
x(1:2) = x_(1:2) + dT*x_(3:4);
x(3:4) = x(3:4) + beta/dT*(delta - x(1:2));
x(1:2) = x(1:2) + alfa*(delta - x(1:2));
end
end
%данные поступают на выход фильтра
corr = x;
t_corr = t;
end
3 ЛАБОРАТОРНАЯ РАБОТА. МОДЕЛИРОВАНИЕ СИСТЕМЫКЭНС
Необходимо промоделировать работу системы КЭНС по высотам рельефа местности в пакете Matlab-Simulink.
Примерный состав данной системы (рисунок 6):
- Модуль полета ЛА вдоль некоторой траектории;
- Модуль измерения радио- и баровысотомеров;
- Модуль работы БИНС;
- Модуль работы КЭНС;
- Модуль работы α - β фильтра.
Также в модели используется блок начальной инициализации данных – 6.
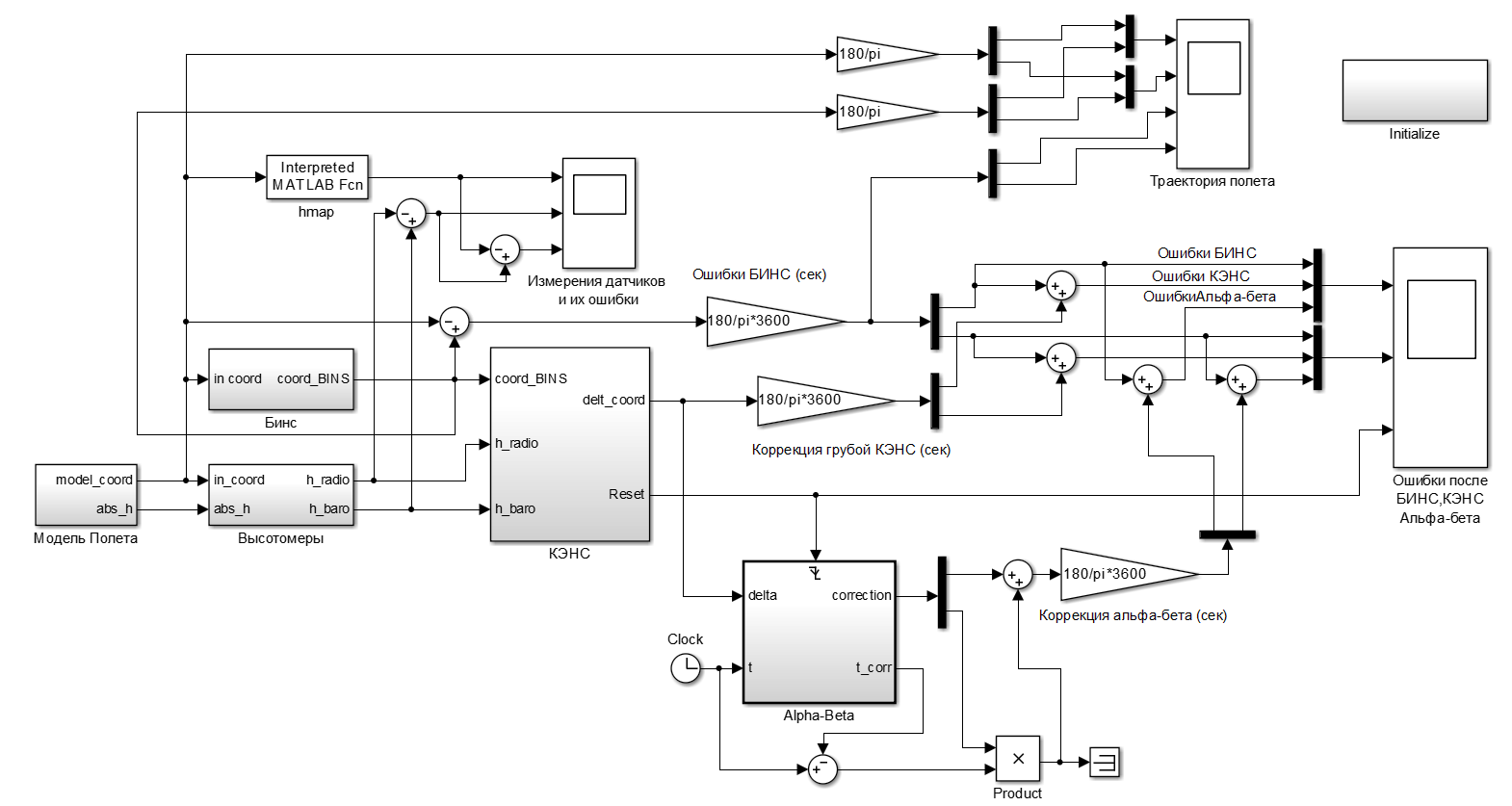
Рисунок 6 – Схема, моделирующая работу системы КЭНС в пакете Matlab-Simulink