Лекции по теории и приложениям искусственных нейронных сетей
Сергей А. Терехов
Лаборатотория Искусственных Нейронных Сетей НТО-2, ВНИИТФ, Снежинск
ЛЕКЦИЯ 8. Модель Хопфилда.
Конфигурация и устойчивость сетей с обратными связями. Модель Хопфилда. Правило обучения Хебба. Ассоциативная память. Распознавание образов.
Модель Хопфилда (J.J.Hopfield, 1982) занимает особое место в ряду нейросетевых моделей. В ней впервые удалось установить связь между нелинейными динамическими системами и нейронными сетями. Образы памяти сети соответствуют устойчивым предельным точкам (аттракторам) динамической системы. Особенно важной оказалась возможность переноса математического аппарата теории нелинейных динамических систем (и статистической физики вообще) на нейронные сети. При этом появилась возможность теоретически оценить об'ем памяти сети Хопфилда, определить область параметров сети, в которой достигается наилучшее функционирование.
В этой лекции мы последовательно начнем рассмотрение с общих свойств сетей с обратными связями, установим правило обучения для сети Хопфилда (правило Хебба), и затем перейдем к обсуждению ассоциативных свойств памяти этой нейронной сети при решении задачи распознавания образов.
Сети с обратными связями
Рассмотренный нами ранее ПЕРСЕПТРОН относится к классу сетей с направленным потоком распространения информации и не содержит обратных связей. На этапе функционирования каждый нейрон выполняет свою функцию - передачу возбуждения другим нейронам - ровно один раз. Динамика состояний нейронов является безитерационной.
Несколько более сложной является динамика в сети Кохонена. Конкурентное соревнование нейронов достигается путем итераций, в процессе которых информация многократно передается между нейронами.
В общем случае может быть рассмотрена нейронная сеть (см. Рис. 8.1), содержащая произвольные обратные связи, по которым переданное возбуждение возвращается к данному нейрону, и он повторно выполняет свою функцию. Наблюдения за биологическими локальными нейросетями указывают на наличие множественных обратных связей. Нейродинамика в таких системах становится итерационной. Это свойство существенно расширяет множество типов нейросетевых архитектур, но одновременно приводит к появлению новых проблем.

Рис. 8.1. Фрагменты сетей с прямым рапространением (A) и с наличием обратных связей (B).
Безитерационная динамика состояний нейронов является, очевидно, всегда устойчивой. Обратные связи могут приводить к возникновению неустойчивостей, подобно тем, которые возникают в усилительных радитехнических системах при положительной обратной связи. В нейронных сетях неустойчивость проявляется в блуждающей смене состояний нейронов, не приводящей к возникновению стационарных состояний. В общем случае ответ на вопрос об устойчивости динамики произвольной системы с обратными связями крайне сложен и до настоящего времени является открытым.
Ниже мы остановимся на важном частном случае нейросетевой архитектуры, для которой свойства устойчивости подробно исследованы.
Нейродинамика в модели Хопфилда
Рассмотрим сеть из N формальных нейронов, в которой степень возбуждения каждого из нейронов Si, i=1..N, может принимать только два значения {-1, +1}. Любой нейрон имеет связь со всеми остальными нейронами Sj, которые в свою очередь связаны с ним. Силу связи от i-го к j-му нейрону обозначим как Wij.
В модели Хопфилда предполагается условие симметричности связей Wij=Wji, с нулевыми диагональными элементами Wii=0. К сожалению, это условие имеет весьма отдаленное отношение к известным свойствам биологических сетей, в которых, наоборот, если один нейрон передает возбуждение другому, то тот, в большинстве случаев, непосредственно не связан с первым. Однако именно симметричность связей, как будет ясно из дальнейшего, существенно влияет на устойчивость динамики.
Изменение состояния каждого нейрона Sj в модели Хопфилда происходит по известному правилу для формальных нейронов МакКаллока и Питтса. Поступающие на его входы сигналы Si в момент t взвешиваются с весами матрицы связей Wij и суммируются, определяя полный уровень силы входного сигнала:

Далее в момент t+1 нейрон изменяет состояние своего возбуждения в зависимости от уровня сигнала h и индивидуального порога каждого нейрона T:

Изменение состояний возбуждения всех нейронов может происходить одновременно, в этом случае говорят о параллельной динамике. Рассматривается также и последовательная нейродинамика, при которой в данный момент времени происходит изменение состояния только одного нейрона. Многочисленные исследования показали, что свойства памяти нейронной сети практически не зависят от типа динамики. При моделировании нейросети на обычном компьютере удобнее последовательная смена состояний нейронов. В аппаратных реализациях нейросетей Хопфилда применятся параллельная динамика.
Совокупность значений возбуждения всех нейронов Si в некоторый момент времени образует вектор состояния S сети. Нейродинамика приводит к изменению вектора состояния S (t). Вектор состояния описывает траекторию в пространстве состояний нейросети. Это пространство для сети с двумя уровнями возбуждения каждого нейрона, очевидно, представляет собой множество вершин гиперкуба размерности, равной числу нейронов N. Возможные наборы значений координат вершин гиперкуба (см. Рис.8.2) и определяют возможные значения вектора состояния.

Рис. 8.2. Проекция 4-х мерного гиперкуба на плоскость. Указанные на рисунке три точки служат примерами возможных состояний нейронной сети из 4-х нейронов.
Рассмотрим теперь проблему устойчивости динамики изменения состояний. Поскольку на каждом временном шаге некоторый нейрон i изменяет свое состояние в соответствии со знаком величины (hi - Ti), то приведенное ниже соотношение всегда неположительно:

Таким образом, оответствующая величина E, являющаяся суммой отдельных значений Ei, может только убывать, либо сохранять свое значение в процессе нейродинамики.

Введенная таким образом величина E является функцией состояния E=E(S) и называется энергетической функцией (энергией) нейронной сети Хопфилда. Поскольку она обладает свойством невозрастания при динамике сети, то одновременно является для нее функцией Ляпунова (А.М. Ляпунов, 1892). Поведение такой динамической системы устойчиво при любом исходном векторе состояния S (t=0) и при любой симметричной матрице связей W с нулевыми диагональными элементами. Динамика при этом заканчивается в одном из минимумов функции Ляпунова, причем активности всех нейронов будут совпадать по знаку с входными сигналами h.
Поверхность энергии E(S) в пространстве состояний имеет весьма сложную форму с большим количеством локальных минимумов, образно напоминая стеганое одеяло. Стационарные состояния, отвечающие минимумам, могут интерпретироваться, как образы памяти нейронной сети. Эволюция к такому образу соотвествует процессу извлечения из памяти. При произвольной матрице связей W образы также произвольны. Для записи в память сети какой-либо осмысленной информации требуется определенное значение весов W, которое может получаться в процессе обучения.
Правило обучения Хебба
Правило обучения для сети Хопфилда опирается на исследования Дональда Хебба (D.Hebb, 1949), который предположил, что синаптическая связь, соединяющая два нейрона будет усиливатьося, если в процессе обучения оба нейрона согласованно испытывают возбуждение либо торможение. Простой алгоритм, реализующий такой механизм обучения, получил название правила Хебба. Рассмотрим его подробно.
Пусть задана обучающая выборка образов x a, a = 1..p. Требуется построить процесс получения матрицы связей W, такой, что соответствующая нейронная сеть будет иметь в качестве стационарных состояний образы обучающей выборки (значения порогов нейронов T обычно полагаются равными нулю).
В случае одного обучающего образа правило Хебба приводит к требуемой матрице:
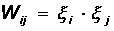
Покажем, что состояние S=x является стационарным для сети Хопфилда с указанной матрицей. Действительно, для любой пары нейронов i и j энергия их взаимодействия в состоянии x достигает своего минимально возможного значения Eij = -(1/2) x i x j x i x j = -1/2.
При этом Е -полная энергия равна E = -(1/2) N 2, что отвечает глобальному минимуму.
Для запоминания других образов может применяется итерационный процесс:

который приводит к полной матрице связей в форме Хебба:

Устойчивость совокупности образов не столь очевидна, как в случае одного образа. Ряд исследований показывает, что нейронная сеть, обученная по правилу Хебба, может в среднем, при больших размерах сети N, хранить не более чем p » 0.14 N различных образов. Устойчивость может быть показана для совокупности ортогональных образов, когда

В этом случае для каждого состояния x a произведение суммарного входа i-го нейрона hi на величину его активности Si = x ai оказывается положительным, следовательно само состояние xa является состоянием притяжения (устойчивым аттрактором):

Таким образом, правило Хебба обеспечивает устойчивость сети Хопфилда на заданном наборе относительно небольшого числа ортогональных образов. В следующем пункте мы остановимся на особенностях памяти полученной нейронной сети.