Лекция 11
Производная по направлению. Градиент функции.
Вопросы:
1. Частные производные высших порядков.
2. Производная по направлению. Градиент.
3. Экстремум функции.
4. Наибольшее и наименьшее значения функции двух переменных.
Частные производные высших порядков
Пусть частные производные fx' (x, y) и fy' (x, y) функции z=f (P), определенной на некотором множестве D, существуют в каждой точке этого множества. В этом случае частные производные представляют собой функции двух переменных x и y, определенные на D. Назовем их частными производными первого порядка.
Определение 5.19. Частные производные по переменным x и y от функций fx' (x, y) и fy' (x, y) в точке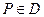 
, если они существуют, называются производными второго порядка относительно функции f (P) в этой точке. Они обозначаются символами
.
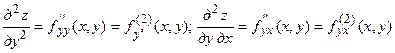Частные производные второго порядка вида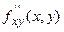 
и 
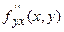называются смешанными частными производными.
Пример 5.11. Найти частные производные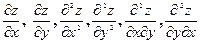 
функции 
.
Решение.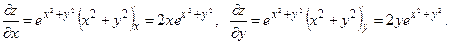 
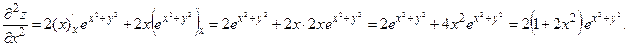
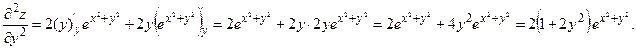
Пример 5.12. Найти частные производные второго порядка функции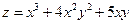 
.
Решение. Имеем: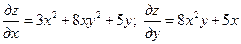 
. Следовательно,
.
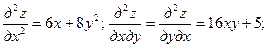
Теорема. Если в некоторой окрестности точки P (x,y) производные 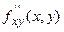и 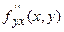существуют и непрерывны в самой точке P, то они равны между собой в этой точке, т.е.
.
Аналогично вводятся понятия частных производных 3-го, 4-го, …, n -го порядков с соответствующей символикой и доказывается теорема о смешанных производных любого порядка.
Производная по направлению. Градиент
Рассмотрим функцию z=f (P), определенную на некотором множестве D и единичный вектор 
произвольного направления.
Рис. 5.4.
Для характеристики скорости изменения функции в точке P (x, y) в направлении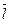 
введем понятие производной по направлению.
Через точку М проведем прямую параллельно вектору 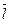и возьмем на ней точку М 1(x+ 
, y+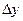 
) (рис.5.4). Функция f (М) получит при этом полное приращение
Δ z = f (x + , y + 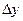)– f (x, y).
Определение 5.20. Предел отношения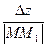 
при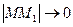 
, (
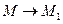), если он существует, называется производной функции z=f (М) в точке М (x, y) по направлению вектора 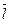и обозначается 
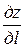, т.е. 
.
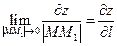Если функция f (М) дифференцируема в точке М, то учитывая, что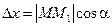 
, 
, производная в данном направлении определяется формулой
. (5.5)
Пример 5.13. Вычислить производную функции z=x 2+ y 2 x в точке P (1;2) по направлению вектора 
, где P 1(3;0).
Решение. Находим единичный вектор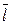 
данного направления:
; 
; 
.
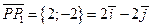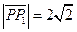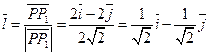Отсюда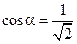 
, 
.
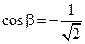Частные производные функции в точке P (1;2):
fx ´(x, y)=2 x + y 2, fy ´(x, y)=2 xy, fx ´(1,2)=6, fy ´(1,2)=4. Следовательно,
.
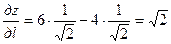Определение 5.21. Градиентом функции z=f (P) в точке P (x, y) называется вектор, проекции которого на координатные оси совпадают с соответствующими частными производными 
, 
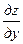, взятыми в точке P (x, y).
Он обозначается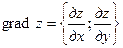 
.
Используя понятие градиента функции, представим формулу (5.5) в виде скалярного произведения векторов
.
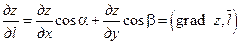Так как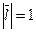 
, то, учитывая определение скалярного произведения, имеем
,
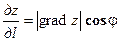где 
— угол между градиентом и вектором .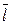
Из последнего равенства следует, что производная функции по направлению будет наибольшей при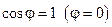 
, т.е. когда направление вектора 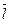совпадает с направлением градиента z, при этом
.
Таким образом, градиент функции z=f (P) в точке P (x, y) характеризует направление и величину максимального роста этой функции в точке P (x, y).
Замечание. Аналогично определяется производная по направлению для функции трех переменных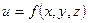 
. При этом справедлива формула
,
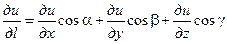где 
— направляющие косинусы, т.е. 
, градиент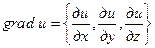 
.
Пример 5.14. Найти производную функции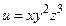 
в точке М (3;2;1) в направлении вектора 
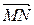, где N (5;4;2).
Решение. Найдем координаты вектора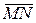 
и его направляющие косинусы:
, 
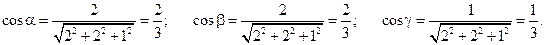
Значения частных производных:
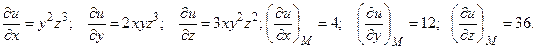
Следовательно,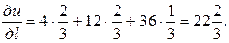 
Градиент в произвольной точке равен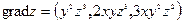 
, а в точке М 
или 