Пусть функция z=f(x, y) непрерывна в ограниченной замкнутой области D и дифференцируема в этой области.
Тогда она имеет в этой области наибольшее и наименьшее значения (глобальный максимум и минимум), которые достигаются или внутри области или на ее границе. Если наибольшее или наименьшее значения функция принимает во внутренних точках D, то эти точки, очевидно, являются точками экстремума функции z=f(x, y). Таким образом, точки, в которых функция принимает наибольшее или наименьшее значения являются либо точками экстремума функции, либо граничными точками области D.
Итак, чтобы найти наименьшее и наибольшее значения функции в ограниченной замкнутой области D, следует определить значение функции в критических точках, лежащих внутри D, а также ее наименьшее и наибольшее значения на границе области D. Наибольшее и наименьшее значение из всех перечисленных значений являются соответственно наибольшим и наименьшим значениями функции z=(x, y) в области D.
Пример 5.17. Найти наибольшее и наименьшее значения функции z= x 2– y 2 в круге x2+y2£4.
Решение. Частные производные первого порядка:

Решая систему уравнений
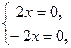
получим одну критическую точку P0(0, 0), в которой значение функции z(P0)=0.
Найдем теперь наибольшее и наименьшее значения функции на границе, т.е. на окружности x2+y2=4. Для точек этой окружности функцию z=x2–y2 можно представить как функцию одной переменной x:
z=x2–(4-x2)=2x2–4,
причем -2£x£2. Следовательно, нахождение наибольшего и наименьшего значений функции двух переменных x2+y2=4 сводится к нахождению наибольшего и наименьшего значений функции одной переменной z=2x2–4 на отрезке [-2;2]. Найдем критические точки этой функции на интервале (-2;2):
 ,
,
откуда получаем критическую точку x=0.
Вычислим значения функции в критической точке и на концах интервала. Имеем
 .
.
Сравнивая значения функции в критической точке P0 внутри области и полученные значения на границе, определяем, что наибольшее значение z= x 2– y 2 в круге x2+y2£4 принимает в точках M1(-2;0) и M2(2;0) окружности x2+y2=4, а наименьшее — в точках M3(0;2) и M4 (0;-2) той же окружности, причем:
zнаиб=4; zнаим=-4.
ЛИТЕРАТУРА
Для содержательных модулей
1. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.
2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. — М.: Наука, 1988.
Основная
1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.
2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.
3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.
4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.
5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.
6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.
7. Руководство к решению задач с экономическим содержанием по курсу высшей математики./ Под ред. А.И. Карасева и Н.Ш. Кремера. — М.: Экономическое образование, 1989.
8. Данко П.Е., Попова А.Г. Высшая математика в упражнениях и задачах. — М.: Высш.шк., 1974.
Сборники задач
1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.
2. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.