Лекция 12
Метод наименьших квадратов. Условный экстремум. Производные неявных функций.
Вопросы:
1. Условный экстремум.
2. Экстремум функции нескольких переменных (общий случай.)
3. Условный экстремум (общий случай).
4. Метод наименьших квадратов.
Условный экстремум
До сих пор рассматривался экстремум функции в предположении, что x и y — независимые переменные, определенных в D. В подобных случаях максимумы и минимумы называются абсолютными.
Рассмотрим теперь случай, когда переменные, от которых зависит функция 
, связаны некоторым соотношением j (x;y)=0 (уравнением связи). В этих случаях максимумы и минимумы называются условными.
Разрешим уравнение j(x, y)=0 относительно y, получим функцию, зависящую от х:
y=y(x).
Подставляя это выражение в функцию z=f(x, y), получим функцию одной переменной x, т.е. придем к задаче отыскания абсолютного экстремума.
Пример 5.18. Найти экстремум функции двух переменных 
при условии 
Решение. Из уравнения связи 
. Следовательно, 
при 
причем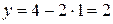 
, 
. Поэтому функция имеет в точке 
минимум 
Этот прием мы применяли в последнем примере при нахождении наибольшего и наименьшего значений функции 
на границе области x2+y2=4. Но разрешение уравнения j(x,y)=0 относительно y бывает иногда затруднительно или даже невыполнимо. Поэтому укажем другой способ решения задачи, метод множителей Лагранжа.
Отыскание условного экстремума сводится в этом случае к исследованию на обычный экстремум так называемой функции Лагранжа
L=f(x,y)+lj(x,y),
где l — неопределенный постоянный множитель (множитель Лагранжа). Необходимыми условиями экстремума будут:
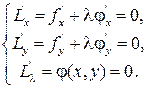
Из этой системы трех уравнений находятся неизвестные значения: x, y, l.
Вопрос о существовании и характере условного экстремума можно решить на основании достаточного условия экстремума для функции Лагранжа. А именно, если 
для функции 
в стационарной точке положителен, то в этой точке имеется условный максимум функции 
, если 
(или 
), и условный минимум, если 
(или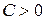 
).
При решении практических задач, в большинстве случаев, наперед ясно какой экстремум будет в критической точке, и поэтому критические точки дополнительно не исследуются.
Пример 5.19. Найти экстремум функции z=x+y при условии, что 
.
Решение. Рассмотрим функцию Лагранжа
Имеем
.
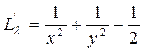Из системы уравнений (необходимое условие экстремума)
находим, что
, 
.
Частные производные второго порядка имеют вид
~ А, 
~ В, 
~С.
Следовательно:
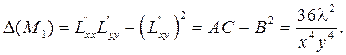
Для точки M1(-2, -2) и l=-4 получаем
Таким образом, M1(-2, -2) — точка максимума.
Для M2(2, 2) и l=4 находим:
Следовательно, M2(2, 2) — точка минимума.
Итак, данная функция z=x+y имеет два условных экстремума:
zmax=z| x = y =-2=-4; zmin=z| x = y =2=4.
В заключение приведем пример применения рассмотренного метода к решению экономических задач.
Пример 5.20. Предприятие располагает двумя способами производства некоторого продукта. Общие издержки производства при каждом способе зависят от произведенных количеств x и y следующим образом:
U1(x)=a0+a1x+a2x2; a0, a1, a2 > 0;
U2(y)=b0+b1y+b2y2; b0, b1, b2 > 0.
Таким образом, суммарные издержки
U(x, y) = U1(x) + U2(y).
За некоторый промежуток времени предприятие должно произвести ровно C единиц продукта, x+y=C, комбинируя его производство различными способами так, чтобы минимизировать общую стоимость. Функция Лагранжа для этой задачи будет
L(x,y,l)=a0+a1x+a2x2+b0+b1y+b2y2+l(C-x-y),
Решая систему, получаем
Здесь необходимо отметить, что эти решения имеют смысл только тогда, когда x0 и y0 неотрицательны. Из написанных выше выражений следует, что это условие выполнено, если
Пример 5.21. Производственная функция Кобба-Дугласа 
не имеет конечного максимума. Но на практике объемы ресурсов ограничены, в этом случае решение соответствующей производственной проблемы сводится к решению задачи на условный экстремум.
Фирма собирается вложить 45000$ в увеличение выпуска продукции, причем стоимость единицы труда – 100$, единицы капитала – 300$. При каком распределении денежных ресурсов фирма получит наибольшее увеличение объема выпуска продукции?
Решение. Согласно условию, надо найти max Q, если 100 L +300 К =45000.
Отсюда L =450–3 K и
Q (K)=50(450–3 K)⅔ K ⅓, где 0≤ K ≤150.
Q ΄(К)=50·⅔·(-3)(450–3 К) - ⅓ К ⅓ +50·⅓(450–3 К)⅔ 
.
После упрощения, получим
Q´(К)= 
.
Приравнивая Q ´(К) к нулю, находим К 1=50, L 1=300.
Для определения наибольшего значения функции Q ´(К) на отрезке [0;150] надо выбрать большее из значений Q (0), Q (50), Q (150).
К 0=0, L 0=450, Q (0)=0.
К 1=50, L 1=300, Q (50)=50·300⅔50⅓=2500·6⅔≈8250.
К 2=150, L 2=0, Q (150)=0.
Таким образом, при вложении 45000$ можно получить увеличение объема производства в 8250 единиц.
Экстремум функции нескольких переменных (общий случай)
Пусть дана дифференцируемая функция u=f(x1,x2,…,x n).
Необходимым условием существования экстремума является обращение в нуль частных производных первого порядка.
Таким образом, координаты критических точек находим, решая систему уравнений
Критические точки являются точками возможного экстремума.
Приведем достаточное условие экстремума.
Рассмотрим определитель
Если главные миноры
положительны, то точка P является точкой локального минимума функции.
Если же D1<0, D2>0, D3<0,…, т.е. знаки главных миноров чередуются в указанном порядке, то P — точка максимума.