В различных исследованиях приходится пользоваться формулами, составленными на основании данного эксперимента. Одним из способов получения таких формул является метод наименьших квадратов.
Пусть на основании данного эксперимента необходимо установить функциональную зависимость между двумя величинами, например, между производительностью труда и себестоимостью продукции. Производим n измерений и по результатам которых составляем таблицу:
| x | x1 | x2 | x3 | … | xn |
| y | y1 | y2 | y3 | … | yn |
При этом вид функции y = f(x) устанавливается или из теоретических исследований, или по характеру расположения на координатной плоскости экспериментальных точек. Пусть, например, точки, взятые из таблицы, группируются около некоторой прямой. В данном случае естественно предположить, что зависимость между x и y линейная y=ax+b.
Эта формула является приближенной, т.к. точки (x1,y1), (x2,y2), …, (x n,y n) могут не лежать на прямой. По методу наименьших квадратов в качестве неизвестных параметров 
выбирают такие значения, при которых сумма квадратов отклонений 
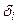теоретических значений 
найденных по эмпирической формуле 
, от соответствующих опытных значений 
т. е. 
была минимальной.
Рассмотрим сумму квадратов отклонений
где x i, y i — заданные числа, коэффициенты a и b — неизвестные величины, подлежащие определению, т.е. S (a, b) можно рассматривать как функцию двух переменных a и b и исследовать ее на экстремум.
Составим систему уравнений
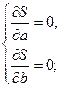или 
(5.5)
После преобразований систему уравнений можно представить в виде
Эта система называется нормальной системой уравнений и имеет единственное решение, так как ее определитель
(а точнее 
, что можно доказать непосредственным упрощением или методом математической индукции при 
).
Если экспериментальные данные таковы, что при построении графика они примерно располагаются на гиперболе, то можно искать приближенную зависимость в форме
.
Аналогично изложенному выше, может быть получена система двух уравнений для определения неизвестных параметров с, d:
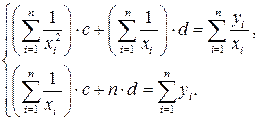
Если экспериментальные данные таковы, что при построении графика они примерно располагаются по параболе, то можно искать приближенную зависимость в форме
y=ax2+bx+c.
Аналогично может быть получена система трех уравнений первой степени для определения неизвестных параметров a, b и c:
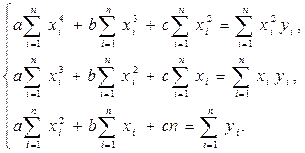
Пример 5.16. Полученные из опыта значения функции y при различных значениях переменной x приведены в таблице
| X | 1,5 | 2,1 | |||
| Y | 2,9 | 6,3 | 7,9 | 10,0 | 13,2 |
Предполагая, что между переменными х и у линейная зависимость, найти эмпирическую формулу вида 
, используя метод наименьших квадратов.
Решение. Построив соответствующие точки, убеждаемся, что они расположены примерно на прямой. Следовательно, зависимость между x и y близка к линейной y=ax+b. Составим расчетную таблицу
| i | x i | y i | 
| xi yi |
| 2,9 | 0,00 | 0,00 | ||
| 1,0 | 6,3 | 1,00 | 6,30 | |
| 1,5 | 7,9 | 2,25 | 11,85 | |
| 2,1 | 10,0 | 4,41 | 21,00 | |
| 3,0 | 13,2 | 9,00 | 39,60 | |
| S | 7,6 | 40,3 | 16,66 | 78,75 |
Составим систему уравнений вида (5.5):
Решая эту систему, находим a =3,42; b =2,86. Отсюда формула искомой прямой
y=3,42x+2,86.
Аналитическая функция, приближенно заменяющая табличные данные, полученные опытным путем, может быть разных видов: обратно-пропорциональной, показательной и т.д.
ЛИТЕРАТУРА
Для содержательных модулей
1. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.
2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. — М.: Наука, 1988.
Основная
1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.
2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.
3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.
4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.
5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.
6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.
7. Руководство к решению задач с экономическим содержанием по курсу высшей математики./ Под ред. А.И. Карасева и Н.Ш. Кремера. — М.: Экономическое образование, 1989.
8. Данко П.Е., Попова А.Г. Высшая математика в упражнениях и задачах. — М.: Высш.шк., 1974.
Сборники задач
1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.
2. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.