Лекция 15
Дифференциальные уравнения первого порядка. Линейные и однородные уравнения первого порядка.
Вопросы:
1. Понятие дифференциального уравнения. Задача Коши. Общее и частное решения.
2. Дифференциальные уравнения первого порядка.
3. Методы решения дифференциальных уравнений первого порядка:
а) дифференциальные уравнения с разделяющимися переменными;
б) дифференциальные уравнения с разделёнными переменными;
в) однородные уравнения;
г) линейные дифференциальные уравнения первого порядка
Изучение предшествующих разделов высшей математики показало, что исследование зависимостей между величинами с помощью математического аппарата удобно производить в том случае, когда эта зависимость задана аналитическим выражением y = f (x). Но иногда в процессе моделирования некоторого экономического явления или процесса получаются другие формы задания соответствующих зависимостей.
Вернемся к изучению вопроса о цене равновесия между спросом d и предложением s. Простейшая математическая модель рассмотрена в первом разделе. Практика показывает, что неизменной цена товара может быть только в течение небольшого промежутка времени. Естественно, что тенденция формирования цены товара р влияет на величину и спроса и предложения s. Математически тенденция формирования цены может быть задана производной по времени 
. Зависимости величины спроса и предложения от цены товара могут быть в этом случае:
.
Приравняв эти выражения, получаем следующее уравнение для определения цены равновесия:
или
.
Как найти из этого уравнения цену в момент времени Т? Что является решением этого уравнения?
Изучению и решению такого типа уравнений посвящен этот раздел курса высшей математики.
Основные определения. Задача Коши. Общее и частное решениЯ
Определение 9.1. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, искомую функцию этих переменных и производные (или дифференциалы) этой функции.
Если независимая переменная одна, то уравнение называется обыкновенным; если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.
Определение 9.2. Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения.
Например:
1) 
— обыкновенное дифференциальное уравнение первого порядка;
2) 
— обыкновенное дифференциальное уравнение второго порядка;
3) 
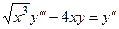— обыкновенное дифференциальное уравнение третьего порядка;
4) 
— дифференциальное уравнение в частных производных первого порядка.
Далее рассматриваются только обыкновенные дифференциальные уравнения, причем слово «обыкновенные» будем опускать.
В общем случае дифференциальное уравнение n –го порядка можно записать следующим образом
, (9.1)
где F — некоторая функция от 
переменных, 
.
Определение 9.3. Дифференциальное уравнение n –го порядка называется разрешенным относительно старшей производной, если оно имеет вид
, (9.2)где f — некоторая функция от 
переменных.
Определение 9.4. Решением дифференциального уравнения n –го порядка называется такая дифференцируемая n раз функция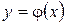 
, которая при подстановке в уравнение вместо неизвестной функции y и ее производных, обращает его в тождество.
Пример 9.1. Решить уравнение 
.
Решение. Запишем уравнение в виде 
. Отсюда 
, тогда 
, где 
— произвольные постоянные.
Пример 9.2. Решить уравнение 
.
Решение. 
,
тогда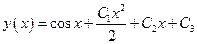 
. Здесь 
— произвольные постоянные.
Отсюда можно предположить, что решение дифференциального уравнения n –го порядка должно зависеть от n произвольных постоянных. Потому, не соблюдая строгости, можно дать следующие определения.
Определение 9.5. Общим решением дифференциального уравнения n –го порядка называется такая функция 
зависящая от 
, которая является решением уравнения при любых значениях постоянных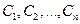 
.
Определение 9.6. Если общее решение задано в неявном виде
,
то оно называется общим интегралом.
Определение 9.7. Частным решением дифференциального уравнения называется решение, полученное из общего решения при некоторых конкретных числовых значениях постоянных 
Определение 9.8. Решение, которое не получатся из общего ни при каких значениях постоянных 
называется особым решением.
Для дифференциального уравнения n –го порядка рассматривается задача Коши, которая ставится так: найти решение дифференциального уравнения (9.1), которое при 
удовлетворяет условиям
где 
— произвольные наперед заданные числа. Взятые вместе числа 
называются начальными данными.
Задача Коши для дифференциального уравнения 1-го порядка:
или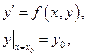 
для уравнения второго порядка:
или 
Определение 9.9. Операция нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения.
Интегрирование дифференциального уравнения зависит от его порядка и вида функции 
.
Далее рассматриваются некоторые виды дифференциальных уравнений, достаточно часто встречающиеся при моделировании экономических процессов и методы их интегрирования.