Определение 9.13. Если правая часть  может быть представлена в виде произведения двух сомножителей, один из которых зависит только от х, второй от у, т.е.
может быть представлена в виде произведения двух сомножителей, один из которых зависит только от х, второй от у, т.е.
f (x, y)= f 1(x)· f 2(y),
то уравнение
dy=f 1(x) ·f 2(y) dx (9.5)
называется дифференциальным уравнением с разделяющимися переменными.
Оно преобразуется к уравнению вида
 ,
,
в котором переменные х и у "разделены". Вычислив первообразные функций
 ,
,
 ,
,
находим общий интеграл такого уравнения
F 2(y)= F 1(x)+ С,
где  .
.
Пример 9.3. Найти зависимость цены на некоторый товар от времени, если известна скорость изменения этой цены  .
.
Решение. Полагая  , f 2(p)= p –30, получаем
, f 2(p)= p –30, получаем
 , т. е.
, т. е.
 .
.
Поскольку интегралы правой и левой части табличные, то нет необходимости в сложных преобразованиях и можно сразу выписать результат
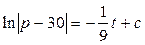 .
.
Разрешая относительно p, получим
 .
.
Если в некоторый исходный момент времени t 0=0 цена товара была известна и р 0=40, можно найти соответствующее частное решение  , отсюда С= 10. Тогда частное решение, удовлетворяющее начальным условиям
, отсюда С= 10. Тогда частное решение, удовлетворяющее начальным условиям  ,
, 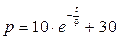 .
.
Пример 9.4. В настоящее время средний темп прироста населения Земли 5 человек на каждую тысячу за год. Определить каким будет население в 2100 году?
Решение. Обозначим x (t) население в момент времени t. Тогда в момент t +Δ t население составит х +Δ х,отношение  — средняя скорость прироста населения.
— средняя скорость прироста населения.
Предел этого отношения при Δ t →0 будет  .
.
По условию х'= 0,005 x и, следовательно, dx= 0,005 xdt, где f 1(t)=0,005, f 2(x)= x, отсюда
 ,
,
 ,
,
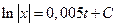
и  — общее решение.
— общее решение.
Подставив начальные условия t 0=2000 и x 0=6·109, найдем С 0:
6·109= С·е 0,005·2000, 6·109= С·е 10 и, значит, С 0=6·109· е -10. Тогда частное решение имеет вид: x= 6·109· e -10· e 0,005 t.
При  находим
находим
 ,
, 
Т.е. если тенденция прироста населения сохранится, то к 2100 оно будет около 10 миллиардов человек.
Замечание. Уравнение вида  с решением
с решением  часто встречаются в практических исследованиях, при описании так называемых процессов «рождения и гибели». В биологии так определяется количество особей в популяции, в медицине — количество заболевших инфекционными заболеваниями, в экономике — количество предметов, находящихся в использовании и т.д.
часто встречаются в практических исследованиях, при описании так называемых процессов «рождения и гибели». В биологии так определяется количество особей в популяции, в медицине — количество заболевших инфекционными заболеваниями, в экономике — количество предметов, находящихся в использовании и т.д.
Например, если стоит задача определения загруженности дорог, необходимо учесть количество автомашин, использующих эти трассы. Коэффициент пропорциональности  , где
, где  — количество автомашин, выпущенных автозаводами (или закупленных населением изучаемого района),
— количество автомашин, выпущенных автозаводами (или закупленных населением изучаемого района),  — количество машин выбывших из употребления (аварии, естественный износ и т.п.).
— количество машин выбывших из употребления (аварии, естественный износ и т.п.).
Пример 9.5. При реализации товара число потенциальных покупателей N человек, в момент времени t товар приобретен x (t) клиентами. Определить тенденцию роста производства для удовлетворения спроса на данный товар.
Решение. Постановка этой задачи похожа на пример 9.4, но необходимо учесть насыщение рынка. Следовательно,
 ,
, 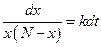 ,
,
 ,
,  .
.
Разрешив относительно х, получим,
 ,
,  .
.
Это уравнение логистической кривой, часто используемой в экономике при описании тенденций роста производства предметов потребления, количества наличных денег в обороте, эффективности рекламы и т.д.
Однородные уравнения
Определение 9.14. Функция  называется однородной функциейстепени n относительно переменных х и y, если при любом
называется однородной функциейстепени n относительно переменных х и y, если при любом  справедливо тождество
справедливо тождество  .
.
Определение 9.15. Уравнение первого порядка 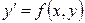 называется однородным относительно x и y, если
называется однородным относительно x и y, если  есть однородная функция нулевой степени относительно x и y.
есть однородная функция нулевой степени относительно x и y.
Полагая 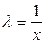 , в силу однородности
, в силу однородности  нулевой степени, получаем
нулевой степени, получаем  Это означает, что уравнение однородное, если его можно представить виде
Это означает, что уравнение однородное, если его можно представить виде

Его решают с помощью замены  т.е.
т.е.  . Тогда
. Тогда  Подставляя в исходное уравнение, получим
Подставляя в исходное уравнение, получим
 .
.
Или  — это уравнение с разделяющимися переменными. Поэтому
— это уравнение с разделяющимися переменными. Поэтому
 .
.
Подставляя после интегрирования  получим общий интеграл исходного уравнения.
получим общий интеграл исходного уравнения.
Пример 9.6. Решить задачу Коши: 
 .
.
Решение. Данное уравнение однородное. Разделив обе его части на х, получим
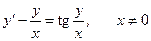 .
.
Сделаем замену  , или
, или  , тогда
, тогда  . Подставляя в уравнение, имеем
. Подставляя в уравнение, имеем

или
 .
.
Решаем полученное дифференциальное уравнение с разделяющимися переменными:
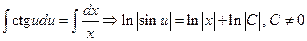 ,
,
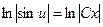 ,
,
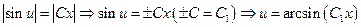 .
.
Сюда включили решение 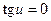 при
при  . Возвращаясь к неизвестной функции y, получаем
. Возвращаясь к неизвестной функции y, получаем  .
.
Используя заданное начальное условие, имеем  , откуда
, откуда  . Итак, искомое частное решение имеет вид
. Итак, искомое частное решение имеет вид  .
.
Ответ.  .
.