Лекция 1.4. Скалярное, векторное и смешанное произведения векторов
Скалярное произведение векторов
Определение 1.1 Скалярным произведением двух векторов 
и 
называется число, равное произведению модулей этих векторов на косинус угла между ними
(1.1)
Скалярное произведение двух векторов можно рассматривать как произведение модуля одного из этих векторов на ортогональную проекцию другого вектора на направление первого 
.
Свойства:
1) 
– действие скалярного произведения коммутативно;
2) 
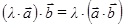– ассоциативно относительно умножения на скаляр;
3) 
– дистрибутивно относительно сложения векторов;
4) 
– скалярный квадрат вектора;
5) если 
то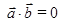 
Если известны координаты векторов 
и 
, то, выполнив разложение векторов по базису 
: 
и 
, найдём
,
т.к. 
, 
, то
(1.2)
.
Условие перпендикулярности векторов: 
.
Пример 1.1 Найти 
, если 
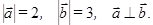
Решение.
Применяя свойства скалярного произведения векторов, получим
.
Пример 1.2 Найти угол между векторами и , если 
.
Решение.
Так как = (1, 2, 3) и = (6, 4, -2), то × = 6 + 8 – 6 = 8,
.
cosj = 
Пример1.3. Найти скалярное произведение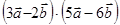 
, если 
Решение.
= 
.
Пример 1.4. Найти угол между векторами и , если 
.
Решение.
Так как 
, 
, то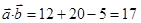 
, 
, следовательно 
Векторное произведение векторов
Обозначения: 
или 
Векторным произведением вектора на вектор в трехмерном евклидовом пространстве называется такой вектор 
, который удовлетворяет условиям:
1) 
(
);
2) вектор 
перпендикулярен плоскости векторов и , т.е. 
, 
;
3) вектор направлен так, что если смотреть с конца вектора , то кратчайший поворот вектора к вектору должен происходить против часовой стрелки 
(векторы , и образуют правую тройку).
|
|
Свойства:
1) 
– действие векторного произведения анти коммутативно;
2) 
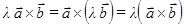– ассоциативно относительно умножения на скаляр;
3) 
– дистрибутивно относительно сложения векторов;
4) Если векторы и коллинеарны, то 
, в частности 
.
Рассмотренные алгебраические свойства позволяют найти аналитическое выражение для векторного произведения через координаты составляющих векторов в ортонормированном базисе 
.
Пусть 
и , тогда
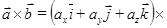
т.к. 
, 
, 
, 
, 
, 
, 
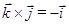, то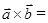 
.
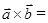
Эту формулу можно записать в форме определителя третьего порядка:
.
Пример 2.1. Найти векторное произведение векторов 
и 
.
Решение. = (2, 5, 1); = (1, 2, -3)
.
Пример 2.3. Найти площадь параллелограмма, построенного на векторах 
,
если 
Решение. 
(ед2).
Некоторые приложения векторного произведения
Определение момента силы относительно точки
Пусть в точке А приложена сила 
и О — некоторая точка пространства (рис. 2.1).
рис. 2.1
Из курса физики известно, что моментом силы 
относительно точки О называется вектор 
, который проходит через точку О и:
1) перпендикулярен плоскости, проходящей через точки О, А, В;
2) численно равен произведению модуля силы на плечо 
3) образует правую тройку с векторами 
и .
Таким образом, 
.
Нахождение линейной скорости вращения
Скорость 
точки М твердого тела, вращающегося с угловой скоростью 
вокруг неподвижной оси, определяется формулой Эйлера 
, где 
, т.О – некоторая неподвижная точка оси (рис. 2.2).
рис. 2.2
Смешанное произведение векторов
Смешанным произведением трех векторов , и 
называется число, равное векторному произведению 
, умноженному скалярно на вектор .
|
|
.
Верно следующее равенство: 
, поэтому смешанное произведение записывают 
или 
.
Как следует из определения, результатом смешанного произведения трёх векторов является число. Это число имеет наглядный геометрический смысл:
Модуль смешанного произведения 
равен объёму параллелепипеда, построенного на приведённых к общему началу векторах , и .
Рис. 3.1. Геометрическая интерпретация смешанного произведения векторов.
Свойства смешанного произведения:
1) 
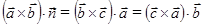, т. е. смешанное произведение не меняется при циклической перестановке векторов;
2) т. е. смешанное произведение не меняется при перестановке знаков векторного и скалярного произведения;
3) 
, т.е. смешанное произведение меняет знак на противоположный при перестановки двух векторов – сомножителей;
4) 
(объём параллелепипеда равен нулю), если векторы 
, 
, 
лежат в одной или параллельных плоскостях, следовательно они компланарны или два из перемножаемых векторов коллинеарны.
5) 
;
6) 
;
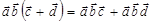7) 
.
Если векторы , , заданы в ортонормированном базисе своими координатами, вычисление смешанного произведения осуществляется по формуле
Выведем формулы вычисления смешанного произведения в координатной форме. Пусть в системе координат 0xyz заданы три вектора: , , 
. Найдем как произведение 
:
= 
Из этой формулы следует условие компланарности векторов , и в координатной форме:
Действительно, если 
, то 
Если векторы , , компланарны, то векторное произведение перпендикулярно вектору . И наоборот, если , то объем параллелепипеда равен нулю, а это возможно только в том случае, когда векторы компланарны (линейно зависимы) или хотя бы один из них является нулевым вектором.
|
|
Таким образом, три вектора компланарны, тогда и только тогда, когда их смешанное произведение равно нулю.
Пример 3.1 Доказать, что точки А(5; 7; -2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.
Найдем координаты векторов: 
. 
, 
Найдем смешанное произведение полученных векторов:
Таким образом, полученные выше векторы компланарны. Следовательно, точки A, B, C и D лежат в одной плоскости.
Пример 3.2 Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).
Найдем координаты векторов: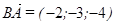 
.
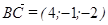Объем пирамиды
Для нахождения длины высоты пирамиды найдем сначала площадь основания BCD.
Sосн = 
(ед2)
Т.к. V = 
; 
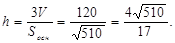(ед3)