ОТЧЁТ
О лабораторной работе №5
по дисциплине: «Экономико-математическое моделирование»
На тему: «Модель рыночной экономики Кейнса»
вариант № 3
Выполнил
студент дневного отделения
факультета менеджмента
II курса 241 группы
Погосян Т.Р.
Гатчина
содержание
Введение
ГЛАВА 1. ОПРЕДЕЛЕНИЕ УСЛОВИЙ РАВНОВЕСИЯ НА РЫНКАХ ДЕНЕГ И ТОВАРОВ
Постановка задачи
1.2. Алгоритм вычисления показателей и экономический анализ полученных результатов
ГЛАВА 2. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ МОДЕЛИ
Постановка задачи
Определение параметров уравнения регрессии с использованием КМНК
2.3 Определение параметров уравнения регрессии с использованием МНК
2.4. Экономический анализ полученных результатов
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
ПРИЛОЖЕНИЯ
Введение
Классическая модель давала ответ на задачу поиска равновесия в экономике в условиях полной занятости. В модели Кейнса показано, что равновесие при полной занятости не является общим случаем. Общий случай - это равновесие при наличии безработицы, а полная занятость лишь особый случай. Но как прийти к равновесию, если экономика при определенном стечении обстоятельств далеко отошла от равновесного состояния и характеризуется массовой безработицей? Чтобы достигнуть желаемого состояния полной занятости, государство обязано проводить особую политику по её достижению, поскольку автоматически действующие рыночные силы без этой поддержки не гарантируют её достижения. Рассмотрим, как определяется равновесное состояние экономики в модели, предложенной Кейнсом.
Целью данной работы является определение условий равновесия на рынках денег и товаров, а также определение параметров модели косвенным методом наименьших квадратов.
Данная работа состоит из введения, двух глав, заключения и двух приложений.
Первая глава посвящена определению условий равновесия на рынках денег и товаров, даётся постановка задачи, вычисляются показатели, и даётся экономический анализ полученных результатов.
Вторая глава работы посвящена определению параметров уравнения функции потребления в простой кейнсианской модели формирования доходов, определяются параметры уравнения регрессии косвенным методом наименьших квадратов, а также даётся экономический анализ полученных результатов.
ГЛАВА 1. ОПРЕДЕЛЕНИЕ УСЛОВИЙ РАВНОВЕСИЯ НА РЫНКАХ ДЕНЕГ И ТОВАРОВ
Постановка задачи
В модели предполагается, что существует три вида активов: деньги, облигации, физический капитал. Относительная цена денег, выраженная в облигациях, - это ставка процента по облигациям. Предполагается, что в условиях равновесия норма прибыли на физический капитал (т.е. на имеющийся запас инвестиционных товаров) равна ставке дохода по облигациям.
Таким образом, появляется возможность проследить, как денежно-кредитная политика влияет на производство. Например, увеличение денежной массы путем печатания новых денег изменяет пропорции обмена между деньгами и облигациями. Если денег станет больше, их будут хранить только при снижении нормы процента на облигации (альтернативный вид активов), при этом норма прибыли также должна снизиться, поскольку облигации и капитал – близкие предметы.
Рассмотрим теперь критерий максимума прибыли по отношению к капиталу (фондам) при фиксированном уровне занятости. Прибыль определяется по формуле:
П = p*F(K, L) – r*К, (1.1)
где р – цена единицы валового внутреннего продукта;
К – капитал, вовлеченный в производство;
L – трудовые ресурсы, вовлеченные в производство;
r – норма прибыли (ставка процента).
Необходимое условие экстремума:
, (1.2)
поскольку 
, то действительно получим условие максимума
(1.3)
т.е. предельная производительность фондов в стоимостном виде равна норме прибыли (ставке процента).
Таким образом, падение нормы прибыли согласно (1.3) означает падение предельного продукта капитала, а поскольку предельный продукт падает с ростом К, то падение нормы прибыли с необходимостью предполагает увеличение спроса на инвестиционные товары, следовательно, и на товары в целом. Проследив всю причинно-следственную цепочку, видим, что сравнительно небольшое увеличение денежной массы приводит к росту спроса на товары, соответственно, к росту предложения товаров, т.е. к увеличению конечного продукта.
Рассмотрим более подробно рынок труда в модели Кейнса. Напомним, что в классической модели равновесие наступало при полной занятости, и равновесное значение реальной заработной платы 
определялось из условия:
(1.4)
При этом равновесный конечный продукт определяется формулой: Y0 = F(K, L0), где L0- число занятых при полной занятости. Предположим теперь, что по определенным причинам спрос Е (на продукцию) оказался меньше предложения Y0 при полной занятости. В этом случае, как считал Кейнс, фактически произведённый конечный продукт Y будет равен спросу: Y = E.Таким образом, фактическая занятость будет меньше полной занятости Y < Y0. Это немедленно окажет влияние на рынок рабочей силы в связи с тем, что при прочих равных условиях меньший объём продукта можно произвести с помощью меньшего числа рабочих, т.е. L < L0.
Таким образом, если в классической модели реальная заработная плата (w/p)0определяла число занятых 
, то в модели Кейнса спрос на товары Е определяет уровень занятости L. При этом ∆L = L0 - L и есть тот уровень безработицы, который диктуется рынками денег и товаров.
Дело в том, что производители не могут продать столько, сколько они хотели бы, но производят и продают только в объёме спроса. Поэтому кривая спроса на рабочую силу, которая выводилась в предположении максимизации прибыли, не может быть применена.
Следовательно, основные новшества модели Кейнса по сравнению с классической моделью состоят в следующем:
1. Равновесие на рынке товаров достигается при равенстве планируемого спроса и фактического предложения.
2. Фактический спрос на рабочую силу определяется фактически востребованным продуктом, и, значит, равновесие на рынке рабочей силы может быть достигнуто тогда, когда рынок товаров находится в равновесии.
В целом модель Кейнса можнозаписать в следующем виде:
Рынок рабочей силы:
LS = LS (w / p), LD = LD(Y 0). (1.5)
Рынок денег:
M S = M S ; M D = k * p * Y + Lq(r), 
< 0, (1.6)
M S = M D, (1.7)
где Lq(r) - спрос на облигации в зависимости от процентной ставки.
Рынок товаров:
Y=Y(L), E=C(Y)+I(r), 
(1.8)
Y=E. (1.9)
При исследовании поведения экономики формулы (1.5) – (1.9) должны быть заменены конкретными зависимостями, отражающими поведение рынков.
Рассмотрим равновесие на рынке товаров, полагая, что зависимости C(Y),I (r)линейные. В этом случае спрос на потребительские товары растёт линейно с ростом предложения товаров:
C(Y) = a + b * Y, (1.10)
где а > 0, 0 < b < 1.
Спрос на инвестиционные товары линейно убывает с ростом нормы процента:
I(r) = d – f * r, (1.11)
где d >0, f > 0.
В этом случае условие равновесия(1.9) запишется в следующей форме:
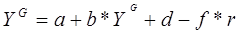, (1.12)
откуда
, (1.13)
т.е. кривая равновесия на рынке товаров (кривая IS ) является линейно-убывающей функцией r и, следовательно, при фиксированном значении rимеется единственное равновесное значение Y G (r ).
Рассмотрим теперь равновесие на рынке денег в предположении, что спрос на облигации Lq(r) линеен:
Lq (r) = h – j*r. (1.14)
Условие равновесия (1.7) при этом запишется в следующем виде:
. (1.15)
Таким образом, кривая равновесия на рынке денег (кривая LM) является возрастающей линейной функцией r,следовательно, при фиксированном r имеется единственное равновесное значение Y M (r).
Общее равновесие на рынках денег и товаров достигается в том случае, когда:
YG (r0) =Y M (r0) = Y0,(1.16)
причём точка равновесия (Y0, r0), т.е. точка пересечения кривых IS и LMединственна.
Общая картина равновесия может быть представлена графически. При этом в первом квадрате изображены кривые IS и LM, а в четвёртом квадрате производственная функция экономики ПФ как функция трудовых ресурсов, в третьем - кривые спроса LD и предложения LS на рабочую силу.
Рис. 1.
На рис. 1. приняты следующие обозначения:
- r0, Y0, L0, (w/p)0, (w/p)n – соответственно, процентная ставка, конечный продукт, занятость, максимальный и минимальный уровни реальной заработной платы при неполной занятости;
- r0, Y0, L0, (w/p)0 – соответственно, процентная ставка, конечный продукт, занятость, уровень реальной заработной платы при полной занятости.
Причинные связи направлены от рынков товаров и денег к рынку рабочей силы через производственную функцию. Причём рынок труда не является определенным. Совокупное равновесие на рынках денег и товаров однозначно определяет фактическую потребность в рабочей силе Y0= F(K, L0) и, если классическая модель предполагает автоматическую тенденцию к полной занятости, то в модели Кейнса таковой нет.
Действительно, пусть равновесие установилось при занятости L0 < L0. Тогда, для того чтобы добиться полной занятости L0,надо увеличить выпуск продукции до Y0 = F(K, L0),что потребовало бы сместить кривую LM в положение LM0 . Как это видно из (1.15), такое смещение можно обеспечить при экзогенно заданном предложении денег MS и фиксированных коэффициентах k и hтолько путём снижения цен р,но никакого механизма снижения цен при фиксированной ставке заработной платы w0 в модели Кейнса не заложено. Следовательно, для перехода к полной занятости нужна специальная государственная политика.
И ещё одна особенность: уровень планируемых расходов Е бывает настолько высок, что производство Y не может достигнуть этого уровня. Это происходит тогда, когда точка пересечения кривых IS и LM имеет отрицательное значение нормы процента.
Коррекцией подхода Кейнса является монетаристский подход к анализу экономики, развитый в начале 70-х годов XX в. Фридменом. Суть различия в подходах Кейнса и Фридмена в следующем. Кейнс считал, что самое значительное влияние на движение основных макроэкономических показателей оказывает спрос на товары, в то время как, по мнению Фридмена, главное - это контроль над предложением денег.
Монетаристы считают, что спекулятивный спрос на деньги не зависит от ставки процента, поэтому увеличение предложения денег приводит к росту цен, но не объёмов производства, как это следовало бы из модели Кейнса. Монетаристы считают, что денежно-кредитная политика не может повлиять в долгосрочном плане на реальный объём производства и безработицу, хотя в краткосрочном плане это возможно.
Как свидетельствует опыт России и других стран, иногда оправдывался подход Кейнса, иногда подход Фридмена. При малой и контролируемой государством инфляции действует кейнсианский подход. При гиперинфляции и слабом контроле государства действует монетаристский подход.
1.2. Алгоритм вычисления показателей и экономический анализ полученных результатов
В качестве изучаемой системы берётся экономика условного объекта.
Исходные данные приведены в таблице 1:
Таблица 1
| a | d | f | b | MS | k | h | j | p | A | |
| 0,31 | 0,25 | 0,3 | 0,51 |
По заданным в таблице 1 значениям: a, b, d, f, используя табличный редактор Excel, рассчитываем по формуле (1.13) зависимость YG = F1(r). Значения r задаём в пределах от 0 до 1,0 с шагом ∆r=0,05. Результаты вычислений представлены в таблице 2:
Таблица 2
| r | YG |
| 0,05 | 291340,58 |
| 0,1 | 274710,14 |
| 0,15 | 258079,71 |
| 0,2 | 241449,28 |
| 0,25 | 224818,84 |
| 0,3 | 208188,41 |
| 0,35 | 191557,97 |
| 0,4 | 174927,54 |
| 0,45 | 158297,10 |
| 0,5 | 141666,67 |
| 0,55 | 125036,23 |
| 0,6 | 108405,80 |
| 0,65 | 91775,36 |
| 0,7 | 75144,93 |
| 0,75 | 58514,49 |
| 0,8 | 41884,06 |
| 0,85 | 25253,62 |
| 0,9 | 8623,19 |
| 0,95 | -8007,25 |
| -24637,68 |
Аналогично производим расчёты значений функции YМ = F2(r), используя формулу (1.15). Численные значения MS, h, j, k, p приведены в таблице 1.
Результаты вычислений приведены в таблице 3:
Таблица 3
| r | YM |
| 78666,67 | |
| 0,05 | 91866,67 |
| 0,1 | 105066,67 |
| 0,15 | 118266,67 |
| 0,2 | 131466,67 |
| 0,25 | 144666,67 |
| 0,3 | 157866,67 |
| 0,35 | 171066,67 |
| 0,4 | 184266,67 |
| 0,45 | 197466,67 |
| 0,5 | 210666,67 |
| 0,55 | 223866,67 |
| 0,6 | 237066,67 |
| 0,65 | 250266,67 |
| 0,7 | 263466,67 |
| 0,75 | 276666,67 |
| 0,8 | 289866,67 |
| 0,85 | 303066,67 |
| 0,9 | 316266,67 |
| 0,95 | 329466,67 |
| 342666,67 |
По полученным данным строим графики зависимостей YG = F1(r) и YМ = F2(r), применив «Мастер диаграмм» табличного редактора Excel (Приложение 1). По точке пересечения этих графиков находим величиныY0 и r0, определяющие равновесие на рынках денег и товаров:
| r0 | 0,4 |
| YG0 | 184266,67 |
 |
Исходя из условия равновесия на рынках денег и товаров, определяем аналитическим путём величину r0 по формуле:
По формуле (1.17) получаем: r0 = 0,38
Сравнивая полученное значение r0 со значением r0, найденным графическим путем, делаем вывод, что они совпадают. Подставляем значение r0 в формулы (1.13) и (1.15) и находим аналитическое значение Y0. Аналитическое значение Y0 = 180134,09. Сравнивая его с Y0, полученным графическим путем, делаем вывод, что они практически совпадают.
Используя производственную функцию вида:
Y=A*L, (1.18)
находим величину L0 по формуле:
(1.19)
Значения величин A и берём из таблицы 1. По формуле (1.19) получаем:
L0 = 3775,08.
Рассчитываем по формуле (1.18) производственную функцию Y = F3(L) и строим её график, используя возможности табличного редактора Excel (Приложение 2). Результаты вычислений приведены в таблице 4:
Таблица 4
| L | Y |
| 87138,73 | |
| 124953,04 | |
| 154281,66 | |
| 179177,07 | |
| 201222,08 | |
| 221232,99 | |
| 239696,79 | |
| 256931,9 | |
| 273160,15 | |
| 288543,46 | |
| 303204,36 | |
| 317238,21 | |
| 330721,01 | |
| 343714,47 | |
| 356269,54 | |
| 368428,85 | |
| 380228,51 | |
| 391699,43 | |
| 402868,32 | |
| 413758,41 |
По значению Y0 находим графическим путем величину L0. Графическое значение L0 = 3775,08. Сравнивая его со значением L0, полученным аналитически, делаем вывод, что они совпадают.
ГЛАВА 2. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ МОДЕЛИ
Постановка задачи
В данной работе необходимо определить в простой кейнсианской модели формирования доходов параметры уравнения функции потребления. Исходная система уравнений имеет вид:
Ct = a + b*Yt + ut; (2.1)
Yt = Ct + It, (2.2)
где t – индекс, указывающий на то, что уравнения (2.1), (2.2) являются системой одновременных уравнений для моментов времени t1-tn;
ut – случайная составляющая;
Ct, Yt – функции потребления и дохода, соответственно являющиеся эндогенными переменными;
It – экзогенно заданная функция, отражающая инвестиционный спрос.
Переменные Ct и Yt являются эндогенными. Эндогенной считается та переменная, значение которой определяется внутри уравнения регрессии, внутри модели. В качестве экзогенной переменной в данной задаче выступают инвестиции It. Экзогенной является та переменная, значение которой определяется вне уравнения регрессии, вне модели и поэтому берется как заданная.
Параметры уравнения регрессии необходимо определить двумя способами:
· косвенным методом наименьших квадратов;
· прямым методом наименьших квадратов.