Определение 4.1 Базисом на прямой называется любой ненулевой вектор, принадлежащий этой прямой.
Определение 4.2 Базисом на плоскости называется любая упорядоченная пара линейно независимых векторов, принадлежащих этой плоскости.
Определение 4.3 Базисом в пространстве называется любая упорядоченная тройка линейно независимых векторов.
Определение 4.4 Базис называется ортогональным, если образующие его векторы попарно ортогональны (взаимно перпендикулярны).
Определение 4.5 Ортогональный базис называется ортонормированным, если образующие его векторы имеют единичную длину.
Пространственный базис, составленный из линейно независимых векторов 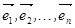 , будем обозначать
, будем обозначать  .
.
Теорема. Пусть дан базис 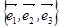 , тогда любой вектор
, тогда любой вектор 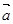 в пространстве
в пространстве  может быть представлен и притом единственным образом в виде
может быть представлен и притом единственным образом в виде  , где
, где 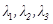 – некоторые числа.
– некоторые числа.
Доказательство.
Докажем вначале существование таких чисел.
Совместим начала всех векторов 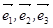 и
и 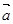 в точке O и проведем через конец вектора
в точке O и проведем через конец вектора  плоскость, параллельную плоскости O,
плоскость, параллельную плоскости O,  (рис. 4.1). Построим новые векторы
(рис. 4.1). Построим новые векторы 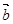 и
и 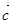 так, что
так, что 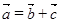 , а
, а 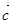 и
и 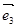 были коллинеарны, тогда в силу коллинеарности векторов
были коллинеарны, тогда в силу коллинеарности векторов 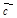 и
и 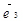 имеем
имеем  . Перенеся затем начало вектора
. Перенеся затем начало вектора 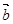 в точку O, получим
в точку O, получим  и, следовательно,
и, следовательно,  что доказывает существование разложения.
что доказывает существование разложения.

Рис. 4.1 Разложения вектора  по базису
по базису 
Докажем единственность разложения по базису. Пусть мы имеем  и допустим, что существует другая тройка чисел
и допустим, что существует другая тройка чисел  таких, что
таких, что 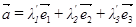
Вычитая почленно эти равенства, получаем

где в силу сделанного предположения о не единственности разложения
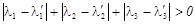
Но полученное неравенство означает, что линейная комбинация
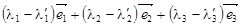
нетривиальна, векторы 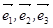 линейно зависимы и, следовательно, не могут быть базисом в силу определения 2.4.1. Полученное противоречие доказывает единственность разложения.
линейно зависимы и, следовательно, не могут быть базисом в силу определения 2.4.1. Полученное противоречие доказывает единственность разложения.
Определение 4.6 Числа 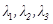 – коэффициенты в разложении
– коэффициенты в разложении  – называются координатами вектора
– называются координатами вектора 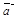 в базисе
в базисе 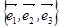
Для сокращенной записи координатного разложения вектора  используются формы:
используются формы:  или
или 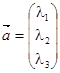
Наконец, если вектор 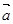 в базисе
в базисе 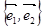 на плоскости может быть представлен как
на плоскости может быть представлен как 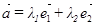 , то его координатная запись имеет вид
, то его координатная запись имеет вид  .
.
Отметим, что указание координат вектора вовсе не фиксирует жестко его положение в пространстве. Координаты вектора лишь отражают его аналитическую связь с базисом, задающим систему координат. В данном случае мы рассматриваем свободные векторы, и любой вектор, полученный из данного путем параллельного переноса, будет иметь те же координаты.
Пример 4.1. Даны векторы 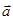 = (1; 2; 3),
= (1; 2; 3),  = (-1; 0; 3),
= (-1; 0; 3), 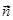 = (2; 1; -1) и
= (2; 1; -1) и 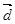 = (3; 2; 2) в некотором базисе. Показать, что векторы
= (3; 2; 2) в некотором базисе. Показать, что векторы 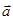 ,
,  и
и 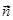 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 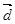 в этом базисе.
в этом базисе.
Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:
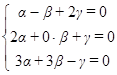 линейно независимы.
линейно независимы.
Тогда  .
.
Это условие выполняется, если определитель матрицы системы отличен от нуля.


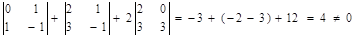
 Для решения этой системы воспользуемся методом Крамера.
Для решения этой системы воспользуемся методом Крамера.
D1 = 
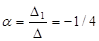 ;
;
D2 = 
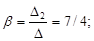
D3 = 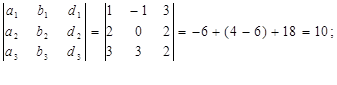
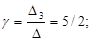
Таким образом, координаты вектора  в базисе
в базисе 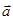 ,
,  ,
, 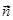 :
:  { -1/4, 7/4, 5/2}.
{ -1/4, 7/4, 5/2}.
Введение базиса в пространстве и на плоскости позволяет поставить в соответствие каждому вектору  упорядоченную тройку (пару) чисел – его координаты. Это, в свою очередь, позволяет установить связь между геометрическими объектами и числами, делает возможным аналитически описывать и исследовать положение и движение физических объектов.
упорядоченную тройку (пару) чисел – его координаты. Это, в свою очередь, позволяет установить связь между геометрическими объектами и числами, делает возможным аналитически описывать и исследовать положение и движение физических объектов.
Базис еще называют репером пространства. Параллельным переносом приведем векторы, образующие базис, к общему началу. Совокупность точки и базиса называют системой координат.
С каждым из базисных векторов можно связать одинаково ориентированную с ним ось. Эти оси и образуют в общем случае так называемую аффинную систему координат (рис. 4.2).

Рис. 4.2. Аффинная система координат.
Если векторы, образующие базис единичны и попарно перпендикулярны, то система координат называется прямоугольной, а базис ортонормированным.
Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.
Впервые прямоугольную систему координат ввел Рене Декартв своей работе «Рассуждение о методе» в 1637году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлеруже в XVIII веке.