Лекция 3. Векторы в пространстве. Линейные операции над векторами. Разложение вектора по базису
Направленные отрезки
Определение 1.1 Отрезок прямой, концами которого служат точки А и В называется направленным отрезком, если указано, какая из этих двух точек является началом и какая – его концом.
Такой направленный отрезок обозначается символом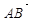 
или 
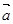. Расстояние между точками А и В называется длиной (модулем) направленного отрезка 
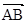и обозначается соответственно 
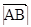или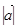 
. Направленные отрезки также называют связанными векторами.
Направленный отрезок, начало и конец которого совпадают, называется нулевым направленным отрезком.
Действия с направленными отрезками
Определение 1.2. Два ненулевых направленных отрезка 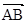и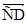 
называются эквивалентными, если их начала и их концы могут быть совмещены параллельным переносом одного из этих отрезков.
То, что направленный отрезок 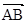имеет ту же длину и направление, что и отрезок 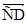обозначается следующим образом: ~ .
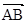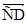Отметим следующие свойства отношения «~»:
1) 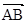~ 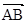(отношение ~ рефлексивно);
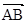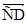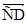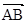2) Если ~ , то ~ (отношение ~ симметрично);
3) Если 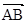~ 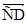, и ~ 
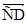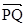, то 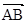~ 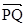(отношение ~ транзитивно).
Таким образом, отношение ~ есть отношение эквивалентности.
Если направленные отрезк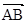и и 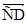эквивалентны, то 
= 
.
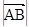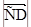Рассмотрим два направленных отрезка 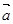и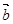 
. Совместим начало направленного отрезка 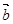с концом отрезка 
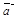(построим направленный отрезок 
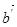, эквивалентный 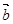, начало которого совпадает с концом отрезка ).
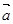Определение 1.3 Суммой двух направленных отрезков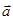 
и 
называется отрезок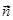 
, начало которого совпадает с началом 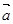и конец с концом .
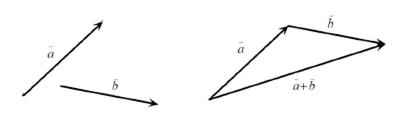
Рис.1.1
Это определение иногда называют правилом треугольника.
Замечание 1. Операция сложения направленных отрезков может быть выполнена по правилу параллелограмма: суммойдвух направленных отрезков 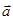и называется отрезок 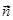, выходящий из их общего начала и являющийся диагональю параллелограмма, построенного на отрезках 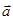и как на сторонах.
|
|
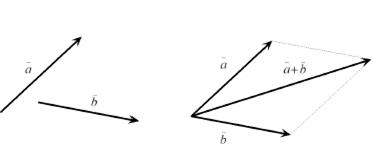
Рис.1.2
Обобщение правила треугольника на любое число слагаемых носит название правила замыкающей.
Чтобы построить сумму любого числа направленных отрезков, нужно в конец 1-го слагаемого направленного отрезка поместить начало 2-ого, в конец 2-ого – начало 3-его и т.д. Направленный отрезок, замыкающий полученную ломаную линию, является суммой. Начало его совпадает с началом 1-ого, а конец – с концом последнего слагаемого направленного отрезка.
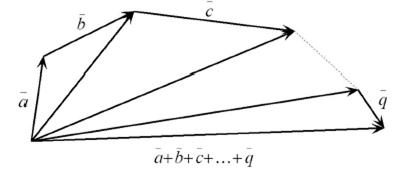
Рис.1.3
Разностью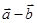 
направленных отрезков 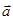и называется направленный отрезок 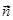, удовлетворяющий условию 
.
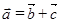Замечание 2. Любой направленный отрезок при сложении с нулевым не изменяется.
Определение 1.3. Под произведением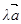 
направленного отрезка на число 
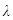понимают:
при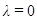 
нулевой направленный отрезок,
при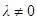 
направленный отрезок, для которого
1) длина равна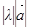 
;
2) направление совпадает с направлением 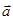, если 
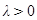, направление противоположно направлению 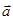, если 
.
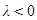Векторы и линейные операции над ними
Определение 2.1 Множество всех направленных отрезков, для которых определены операции сравнения, сложения, умножения на вещественное число, называется множеством векторов. Конкретный элемент этого множества будем называть вектором и обозначать символом с верхней стрелкой, например, 
.
Термин вектор (от лат. Vector – «несущий») впервые появилось в 1845г. в работах ирландского математика Уильяма Гамильтона.
|
|
Нулевой вектор обозначается символом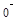 
Операции сложения и умножения на вещественное число на множестве векторов обладают свойствами:
1°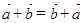 
– коммутативность;
2°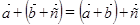 
, 
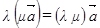– ассоциативность;
3° 
, 
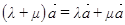– дистрибутивность (для любых векторов 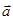, и 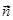и любых вещественных чисел 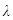и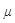 
).