25. Найдите в справочнике формулы сокращенного умножения и запишите их:
 __________________ ___________________________ ____,
__________________ ___________________________ ____,
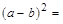 _________________________________________________,
_________________________________________________,
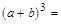 _________________________________________________,
_________________________________________________,
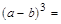 _________________________________________________,
_________________________________________________,
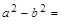 _________________________________________________,
_________________________________________________,
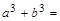 _________________________________________________,
_________________________________________________,
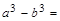 _________________________________________________,
_________________________________________________,
26. Разложите на множители:
Образец: 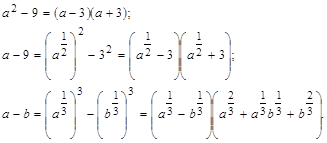
|
а) 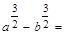
б) 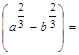
27. Разложите на множители числитель или знаменатель дроби и сократите дробь:
Образец:
 . .
|
а) 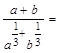
б) 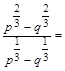
в) 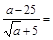
г) 
28. Упростите выражения:
а) 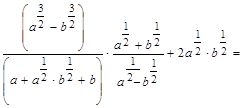
б) 
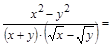
в) 
г) 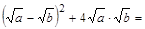
д) 
Линейная функция. Линейные уравнения
И неравенства
29. Построить графики функций (на одном чертеже):
| а) у =2 х +3; | х | ||
| у |
| б) у = –3 х; | х | ||
| у |
| в) у =5. | х | ||
| у |
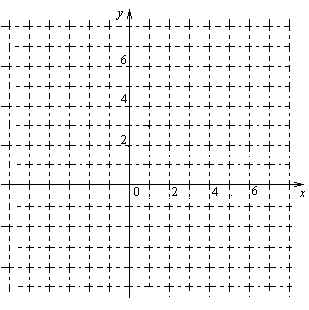 |
Указания: прочтите в справочнике материал по теме «Линейная функция и её график», постройте графики в декартовой системе координат, составив для графика таблицу из двух контрольных точек.
30. Упростите выражения:
1) 3 (4 –2 х) + 7 (1 – х) =
2) 8 (х –2) – 4 (1 –2 х) =
31. Решите уравнения
а) 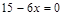 ;
;
б) 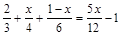 .
.
Указание: упростите уравнение, умножив обе части на наименьшее общее кратное чисел 3, 4, 6 и 12.
32. Решите неравенства устно и запишите ответ:
| 1) х + 3 < 2 | 2) х – 2 > – 3 |
| Ответ: | Ответ: |
| 3) – 2 х < 6 | 4) х + 2 > – 3 х |
| Ответ: | Ответ: |
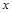 33. Решите неравенство и изобразите множество его решений на числовой оси:
33. Решите неравенство и изобразите множество его решений на числовой оси:
| 1) 3 х + 7 < 13 | 2) 6 х – 5 > 13 |
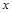  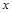 
| |
| 2) 2 – 3 х < 14 | 4) 11 – 4 х > 19 |
  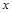 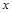
|
34. Решите неравенства
| 1) 6 (х –5) > 2(х– 3); | 2) 7(у +1) < 9(у –3); |
3) 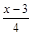 < 3; < 3;
| 4) 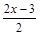 > > 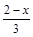 . .
|
35. Найдите наибольшее целое число, являющееся решением неравенства и укажите в ответе.
| 1) 5 – 6 х > 2(4– х) | 2) 6(1– х) > х –1 |
| Ответ: | Ответ: |
36. Найти наименьшее целое число, являющееся решением
неравенства и укажите в ответе.
| 1) 3,2 х – 2 > 2 х + 0,4 | 2) 5,5 + 4 х > 1 + х |
| Ответ: | Ответ: |
37. Заполните таблицу:
 Двойное неравенство Двойное неравенство
| Числовой промежуток | Изображение на числовой оси |
| -9 < х < 0 | (–9; 0) | –9 0 |
| – 3 ≤ х < 7 | ||
–0,5 < х  6 6
| ||
– 11  х х  11 11
| ||
| (-5; 5 ] | ||
| (1,2; 3,5) | ||
[– 4 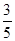 ; –1 ; –1 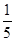 ] ]
| ||
| [0,6; 9] | ||

| –2,5 –1 | |

| –12 12 | |

| –3,7 2,7 | |

| 1 6,5 |
Квадратичная функция. Квадратные уравнения
И неравенства
38. Найдите в справочнике формулу для отыскания корней квадратного уравнения и запишите её:
 D=
D= 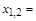
39. Заполните таблицу:
| № | Уравнение

| 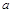
| 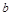
| 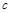
| 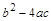
| 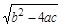
|
| х 2 –5 х +4 = 0 | -5 | (–5)2– 4.1. 4 = 4 | ||||
| х 2 +6 х + 8 = 0 | ||||||
| 2 х 2 + 3 х – 2 = 8 | ||||||
| – х 2 + 7 х + 18 = 0 | ||||||
| – 2 х 2 + 7 х – 3 = 0 | ||||||
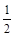 х 2 – 2 = 0 х 2 – 2 = 0
| ||||||
– 3 х 2 + 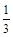 = 0 = 0
| ||||||
| 5 х 2 – х = 0 | ||||||
| х 2 –6 х + 9 = 0 |
40. Заполните таблицу:
| № | Уравнение

| 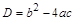
| Количество корней |
| х 2 –2 х + 3 = 0 | (–2)2 – 4. 1. 3 = –8 < 0 | корней нет | |
| х 2 + 7 х – 1 = 0 | |||
| 2 х 2 - 3 х + 5 = 0 | |||
| -3 х 2 + х – 2 = 0 | |||
 х 2 – 3 х – 6 = 0 х 2 – 3 х – 6 = 0
|
41. Завершите решение уравнений:
| 1) х 2 + 4 х – 12 = 0 | 2) х 2 – 4 х – 21 = 0 |
| а = 1, b = 4, с = –12 | а =…, b =…., с =….. |
| х 1, 2 = | х 1, 2 = |
| х 1= х 2 = | х 1= х 2 = |
42. Решите уравнения:
| 1) 2 х 2 + 7 х – 4 = 0; | 7) 4 х 2 – 20 х + 25 = 0; |
| 2) 3 х 2 – х – 2 = 0; | 8) 25 х 2 – 10 х + 2 =0; |
| 3) 9 х 2 + 6 х + 1 = 0; | 9) 12 х 2 – 5 х – 2 = 0; |
| 4) – 4 х 2 + 12 х – 9 = 0; | 10) 15 х 2 + 7 х – 2 = 0; |
| 5) 5 х 2 – 6 х + 2 = 0; | 11) 5 х 2 – 3 х = 0; |
| 6) 3 х 2 + 4 х + 7 = 0; | 12) 4 х 2 – 9 = 0; |
43. Решите уравнения:
| 1) х (х + 2) = 6 + х – х 2; |
2) 2 х – х 2 – 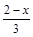 = 0; = 0;
|
3)  – – 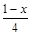 + + 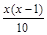 = 0; = 0;
|
4) х 2 – 3 = 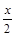 + 2; + 2;
|
5) 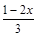 = х 2 –– = х 2 –– 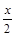 ; ;
|
6) 2 х 2 + х = 1 – 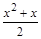 ; ;
|
7) 2 х 2 – 2 х – 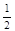 = = 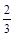 х 2 – х 2 – 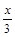
|
44. Постройте графики функций:
а) 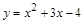 ; б)
; б) 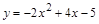
Указание: прочтите в справочнике материал по теме «Квадратичная функция и её график». для построения каждой параболы выполните следующие пункты плана.
а)  ; ;
| б) 
| ||||||||||||
| 1)Укажите направление ветвей каждой параболы | |||||||||||||
| 2)Найдите координаты вершин каждой параболы | |||||||||||||
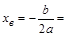
| 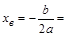
| ||||||||||||
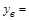
| 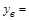
| ||||||||||||
| 3) Найдите нули функций, решив квадратное уравнение | |||||||||||||

| 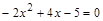
| ||||||||||||
| 4) Составьте таблицы контрольных точек | |||||||||||||
| х | х | ||||||||||||
| у | у | ||||||||||||
5) постройте параболы | |||||||||||||

45. Определите взаимное расположение графиков функций 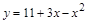 и
и  . если графики имеют общие точки, найдите их координаты.
. если графики имеют общие точки, найдите их координаты.
Указания: 1) прочтите в справочнике тему «Квадратичная функция и её график» и решение систем квадратных уравнений.
2) для определения общих точек графиков функций составьте систему квадратных уравнений
3) Решите систему методом исключения неизвестной, для этого приравняйте правые части уравнений и решите получившееся квадратное уравнение.
Ответ:
46. Определите взаимное расположение графиков функций:
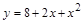 и
и 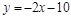 .
.
Указания: 1) Составьте систему уравнений для определения общих точек.
2) Решите полученную систему методом исключения.
Ответ:
47. Разложите квадратные трёхчлены на линейные множители и заполните таблицу:
| № | Квадратный трехчлен

| Корни уравнения
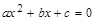
| Разложение а на множители |
| 5 х 2 –9 х– 2 | х 1,2 = 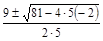 х 1 =
х 1 = 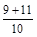 = 2
х 2 = = 2
х 2 = 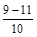 = - = - 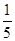
|
5(х– 2) (х + 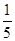 ) )
| |
| –5 х2 – 9 х + 2 | |||
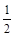 х2– х – 12 х2– х – 12
| |||
– 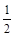 х 2 + 4 х – 8 х 2 + 4 х – 8
| |||
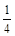 х 2 – 3 х + 2,25 х 2 – 3 х + 2,25
| |||
– 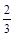 х2 – х + 3 х2 – х + 3
|
48. Разложите квадратные трёхчлены на линейные множители и сократите дроби:
1) 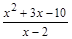 = = 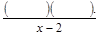 х 2 + 3 х – 10 = 0,
х 1 =, х 2 = ;
х 2 + 3 х – 10 = 0,
х 1 =, х 2 = ;
|
2) 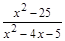 = =
|
3) 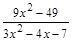 = =
|
49. Укажите, при каких значениях х функция, заданная графически, принимает значения, указанные в первом столбце таблицы, и заполните соответствующие строки таблицы.

|
|

| |

| 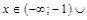 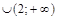
| 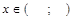
| 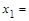 ; ;
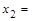 . .
|
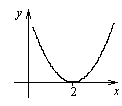
| |||
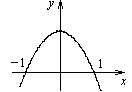
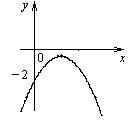
|
50. Заполните пустые клетки таблицы, указав знаком ↑ или ↓
направление ветвей параболы
| Функция | у = 1 – х 2 | у = 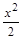 + 3 х –1 + 3 х –1
| у= –5 х 2 + х + 1 | 
|
 Направление ветвей параболы Направление ветвей параболы
|
51. Решить квадратные неравенства с помощью эскиза графика квадратичной функции:
Образец:
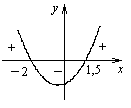
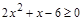
Введём функцию 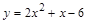 .
.
Ветви параболы направлены вверх.
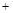
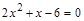 при
при 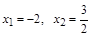
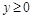 при
при 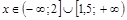 .
.
Ответ:  .
.
1) 4 х – х 2 > 0;

|
2) х 2 + 2 х – 15 ≥ 0;

|
3) 3 х 2 + 14 х ≤ 0;

|
4) 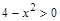 ; ;

|
5) 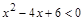 ; ;

|
6) 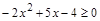 ; ;

|
7) 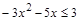 ; ;

|
8) 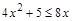 . .

|