Так как теоретически показали, что время работы всех алгоритмов в среднем O (log N), то следует ожидать при тестировании почти всегда результаты отличающиеся на константу.
Проведем исследования зависимости времени работы алгоритмов от размеров задачи при равномерном распределении точек:
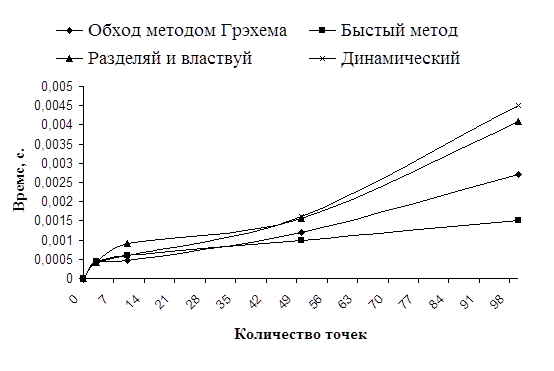
Рис. 5: Зависимость время выполнения алгоритмов при равномерном случайном расположении точек (N<=100).
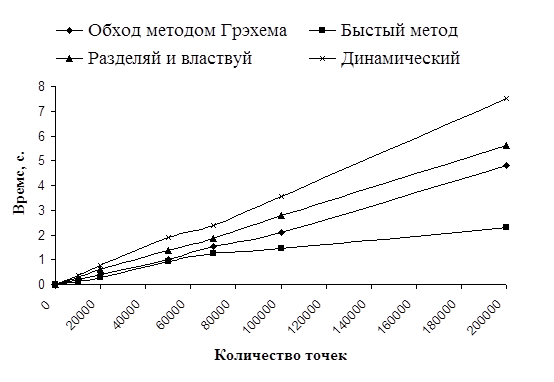
Рис. 6: Зависимость время выполнения алгоритмов при равномерном случайном расположении точек (N<=200000).
Как видно из диаграмм, все алгоритмы в среднем при равномерном распределении точек показали почти линейное время. Различается время примерно в одинаковое число раз, что связано с реализацией данных алгоритмов. Так же видно, при данном распределении быстрее всех работает быстрый алгоритм построения выпуклой оболочки. Это объясняется тем, что в этом случае при каждом шаге он отбрасывает примерно одинаковую часть точек. Поэтому на каждом i -том уровне рекурсии происходит обработка Nki точек, где k часть вершин, которая остается. Это k будет меньше единицы, и не будет сильно изменяться на более глубоких вызовах рекурсивной процедуры. Отсюда получаем то, что время будет стремиться к линейному.
Такого не должно наблюдаться при тестах, в которых почти все данные точки будут являться вершинами выпуклой оболочки.
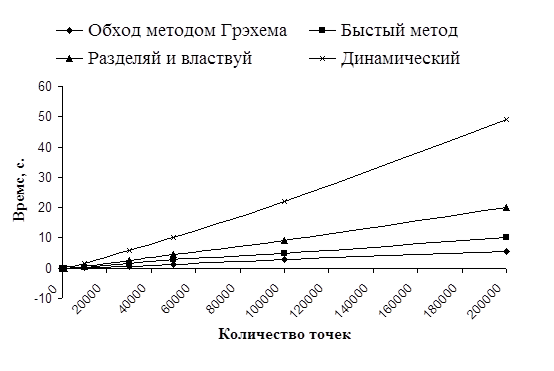
Рис. 7: Зависимость время выполнения при расположении точек на окружности.
Как видно в данном случае алгоритм Грэхема оказался самым эффективным. Быстрый метод в этом случае не выбрасывает на каждом шаге точек, но так как делит их примерно на равные части, то получается, что он работает примерно время O (N log N), что вполне приемлемо. Что касается динамического построения, то в процессе добавления точек в дерево попадают все вершины, а так как при работе с AWL деревом в моей реализации используются сложные операции с указателями то и процедура получилась медленной.
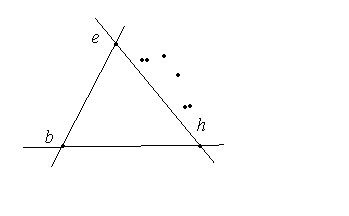
Рис. 8: Нежелательный случай расположения точек для быстрого алгоритма.
Из алгоритма быстрого построения следует, что в некоторых случая на каком-то шаге может оказаться, что не была удалена ни одна вершина, и все точки оказались по одну сторону от bh и eh (рис. 8). Если такое случается очень редко, то это не отразится на времени выполнения значительно, а если такое происходит на каждом шаге, то это приводит к оценке O (N 2). Для моей реализации этого алгоритма можно взять график ex и точку, расположенную на оси ординат над точкой O.

Рис. 9: Время работы быстрой оболочки O (N 2).
Выводы
Как видно из результатов тестов, быстрый метод с данной задачей справляется неудовлетворительно.
Теперь можно подвести итоги. В большинстве случаев самыми быстрыми являются алгоритмы Грэхема и быстрый алгоритм. С учетом того, что они просты для реализации, они вполне приемлемы для многих задач.
Но быстрый метод имеет существенный недостаток. Если нас интересует поведение алгоритма в худшем случае, он неприемлем.
Алгоритм типа “разделяй и властвуй” не показал очень быстрых результатов и не является очень простым в реализации, но он в худшем случае все равно имеет оптимальную оценку. Так же он может быть очень эффективно распараллелен.
Динамический способ стоит реализовывать только в случае, если требуется открытый алгоритм, так как он не является очень быстрым и его реализация связана с различными трудностями.
Заключение
В этой работе были показаны основные алгоритмы построения выпуклых оболочек на плоскости. Так же были проведены сравнения на конкретных реализациях алгоритмов и тестах. Все задачи, поставленные перед этой работой, на мой взгляд, решены.
Приложение Unit1.pas
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
ExtCtrls, StdCtrls, Spin;
const timew=10/24/60/60;
type
tp=extended;
pr=^rr;
rr=record
x,y:tp;
n:pr;
end;
TForm1 = class(TForm)
Panel1: TPanel;
ResetButton: TButton;
PaintBox1: TPaintBox;
RandomButton: TButton;
Label2: TLabel;
Label1: TLabel;
Label3: TLabel;
QRandom: TSpinEdit;
Range: TSpinEdit;
GrahamButton: TButton;
TimeL: TLabel;
QButton: TButton;
DiveRule: TButton;
Circle: TButton;
Button1: TButton;
Button2: TButton;
Button3: TButton;
procedure PaintBox1Paint(Sender: TObject);
procedure RandomButtonClick(Sender: TObject);
procedure ResetButtonClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure GrahamButtonClick(Sender: TObject);
procedure PaintBox1MouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
procedure QButtonClick(Sender: TObject);
procedure DiveRuleClick(Sender: TObject);
procedure CircleClick(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
cn,sn:pr;
mx,my:tp;
strr:string;
x0,y0:integer;
time:double;
tt:pr;
kkk:integer;
implementation
{$R *.DFM}
procedure Writ(x,y:tp);
var t:pr;
begin
new(t);
t^.x:=x;
t^.y:=y;
t^.n:=sn;
sn:=t;
end;
procedure TForm1.PaintBox1Paint(Sender: TObject);
var t:pr;
rect:TRect;
x,y:integer;
begin
with PaintBox1 do
begin
Canvas.Brush.Color:=clBtnFace;
rect.Left:=0;
rect.Top:=0;
rect.Bottom:=Height;
rect.Right:=Width;
Canvas.FillRect(rect);
Canvas.Pen.Color:=clGray;
x0:=Width div 2;
y0:=Height div 2;
Canvas.MoveTo(x0,y0);
Canvas.LineTo(x0,0);
Canvas.MoveTo(x0,y0);
Canvas.LineTo(x0,Height);
Canvas.MoveTo(x0,y0);
Canvas.LineTo(0,y0);
Canvas.MoveTo(x0,y0);
Canvas.LineTo(Width,y0);
Canvas.Pen.Color:=clGreen;
if sn<>nil then
begin
t:=sn;
x:=x0+Trunc(t^.x*mx);
y:=y0+Trunc(t^.y*my);
Canvas.MoveTo(x,y);
while t<>nil do
begin
x:=x0+Trunc(t^.x*mx);
y:=y0+Trunc(t^.y*my);
Canvas.LineTo(x,y);
t:=t^.n;
end;
x:=x0+Trunc(sn^.x*mx);
y:=y0+Trunc(sn^.y*my);
Canvas.LineTo(x,y);
end;
Canvas.Pen.Color:=clBlue;
t:=cn;
while t<>nil do
begin
x:=x0+Trunc(t^.x*mx);
y:=y0+Trunc(t^.y*my);
Canvas.Ellipse(x-1,y-1,x+1,y+1);
t:=t^.n;
end;
end;
end;
procedure TForm1.RandomButtonClick(Sender: TObject);
var
i:integer;
t:pr;
begin
randomize();
while cn<>nil do
begin
t:=cn^.n;
dispose(cn);
cn:=t;
end;
while sn<>nil do
begin
t:=sn^.n;
dispose(sn);
sn:=t;
end;
mx:=0;
my:=0;
for i:=1 to QRandom.Value do
begin
new(t);
t^.n:=cn;
cn:=t;
t^.x:=random(2*Range.Value+1)-Range.Value;
t^.y:=random(2*Range.Value+1)-Range.Value;
if mx<abs(t^.x) then mx:=abs(t^.x);
if my<abs(t^.y) then my:=abs(t^.y);
end;
if mx<>0 then mx:=0.8*(Width div 2)/mx;
if my<>0 then my:=0.8*(Height div 2)/my;
PaintBox1.Refresh;
end;
procedure TForm1.ResetButtonClick(Sender: TObject);
var
t:pr;
begin
while cn<>nil do
begin
t:=cn^.n;
dispose(cn);
cn:=t;
end;
while sn<>nil do
begin
t:=sn^.n;
dispose(sn);
sn:=t;
end;
mx:=1;
my:=1;
PaintBox1.Refresh;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
cn:=nil;
sn:=nil;
mx:=1;
my:=1;
with PaintBox1 do
begin
x0:=Width div 2;
y0:=Height div 2;
end;
end;
procedure TForm1.GrahamButtonClick(Sender: TObject);
label repl;
type
prec=^rec;
rec=record
x,y:tp;
next,prev:prec;
end;
var st,t,s,l,r,p:prec;
procedure inss(var st:prec;t,d:prec);
begin
if st=nil then
begin
st:=t;
d^.next:=t;
st^.prev:=d;
end else
begin
st^.prev^.next:=t;
d^.next:=st;
t^.prev:=st^.prev;
st^.prev:=d;
end;
end;
procedure ins(var st,t:prec);
begin
if st=nil then
begin
st:=t;
st^.next:=t;
st^.prev:=t;
end else
begin
t^.next:=st;
t^.prev:=st^.prev;
st^.prev^.next:=t;
st^.prev:=t;
end;
end;
procedure cut(var st,t:prec);
begin
if st^.next=st then st:=nil else
begin
if t=st
then st:=t^.next;
t^.next^.prev:=t^.prev;
t^.prev^.next:=t^.next;
end;
end;
procedure sort(var b:prec;e:prec);
var p,q:prec;
x:tp;
begin
if b=e then exit;
if b^.next=e then
begin
if (b^.x>e^.x) or ((b^.x=e^.x)and(b^.y>e^.y)) then
begin
x:=b^.x;
b^.x:=e^.x;
e^.x:=x;
x:=b^.y;
b^.y:=e^.y;
e^.y:=x;
end;
exit;
end;
p:=b;
q:=e;
while (p<>q)and(p^.next<>q) do
begin
p:=p^.next;
q:=q^.prev;
end;
if p=q then q:=q.next;
p^.next:=b;
b^.prev:=p;
q^.prev:=e;
e^.next:=q;
sort(b,p);
sort(q,e);
p:=b;
b:=nil;
while (p<>nil)and(q<>nil) do
begin
if (p^.x>q^.x)or((p^.x=q^.x)and(p^.y>q^.y)) then
begin
e:=q;
cut(q,e);
ins(b,e);
end else
begin
e:=p;
cut(p,e);
ins(b,e);
end;
end;
if p<>nil then
begin
e:=p;
inss(b,e,e^.prev);
end;
if q<>nil then
begin
e:=q;
inss(b,e,e^.prev);
end;
end;
procedure sort2(var b:prec;e:prec);
var p,q:prec;
x:tp;
begin
if b=e then exit;
if b^.next=e then
begin
if (b^.x<e^.x) or ((b^.x=e^.x)and(b^.y<e^.y)) then
begin
x:=b^.x;
b^.x:=e^.x;
e^.x:=x;
x:=b^.y;
b^.y:=e^.y;
e^.y:=x;
end;
exit;
end;
p:=b;
q:=e;
while (p<>q)and(p^.next<>q) do
begin
p:=p^.next;
q:=q^.prev;
end;
if p=q then q:=q.next;
p^.next:=b;
b^.prev:=p;
q^.prev:=e;
e^.next:=q;
sort2(b,p);
sort2(q,e);
p:=b;
b:=nil;
while (p<>nil)and(q<>nil) do
begin
if (p^.x<q^.x)or((p^.x=q^.x)and(p^.y<q^.y)) then
begin
e:=q;
cut(q,e);
ins(b,e);
end else
begin
e:=p;
cut(p,e);
ins(b,e);
end;
end;
if p<>nil then
begin
e:=p;
inss(b,e,e^.prev);
end;
if q<>nil then
begin
e:=q;
inss(b,e,e^.prev);
end;
end;
procedure grah(var st:prec);
var r,t,g:prec;
f:integer;
begin
if st^.next=st^.prev then exit;
r:=st;
t:=st;
f:=0;
while (f<=0) or (t<>r) do
begin
if (t^.next^.x-t^.prev^.x)*(t^.y-t^.prev^.y)>=(t^.x-t^.prev^.x)*(t^.next^.y-t^.prev^.y) then
begin
if t=r then
begin
dec(f);
r:=t^.next;
end;
t:=t^.prev;
g:=t^.next;
cut(st,g);
dispose(g);
end else
begin
t:=t^.next;
if t=r then inc(f);
end;
end;
end;
begin
time:=now;
kkk:=0;
repeat
while sn<>nil do
begin
tt:=sn^.n;
dispose(sn);
sn:=tt;
end;
st:=nil;
s:=nil;
tt:=cn;
if tt=nil then exit;
while tt<>nil do
begin
new(t);
t^.x:=tt^.x;
t^.y:=tt^.y;
tt:=tt^.n;
ins(st,t);
end;
if st=nil then exit;
l:=st;
r:=st;
t:=st;
repeat
if (r^.x<t^.x) or ((r^.y<t^.y)and(r^.x=t^.x)) then r:=t;
if (l^.x>t^.x) or ((l^.y>t^.y)and(l^.x=t^.x)) then l:=t;
t:=t^.next;
until t=st;
if l^.x=r^.x then
begin
str((now-time)*24*60*60:0:2,strr);
TimeL.Caption:=strr+'s';
writ(l^.x,l^.y);
if not((r^.x=l^.x)and(r^.y=l^.y)) then writ(r^.x,r^.y);
t:=l;
while l<>nil do
begin
t:=l;
cut(l,t);
dispose(t);
end;
exit;
end;
t:=l;
t:=st;
repeat
repl:
if st=nil then break;
p:=t;
t:=t^.next;
if (p^.x-l^.x)*(r^.y-l^.y)<=(p^.y-l^.y)*(r^.x-l^.x) then
begin
cut(st,p);
ins(s,p);
goto repl;
end;
until t=st;
sort2(s,s^.prev);
if st <> nil then
begin
sort(st,st^.prev);
t:=st^.prev;
st^.prev^.next:=s;
st^.prev:=s^.prev;
s^.prev^.next:=st;
s^.prev:=t;
st:=st^.prev;
grah(s);
end;
t:=s;
repeat
writ(t^.x,t^.y);
t:=t^.next;
until t=s;
while s<>nil do
begin
t:=s;
cut(s,t);
dispose(t);
end;
inc(kkk);
until now-time>timew;
str((now-time)/kkk*24*60*60:0:6,strr);
TimeL.Caption:=strr+'s';
PaintBox1.Refresh;
end;
{ end graham}
procedure TForm1.PaintBox1MouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
var
t:pr;
begin
new(t);
t^.x:=(x-x0)/mx;
t^.y:=(y-y0)/my;
t^.n:=cn;
cn:=t;
Canvas.Pen.Color:=clBlue;
Canvas.Ellipse(x-1,y-1,x+1,y+1);
end;
{-------------------------------------}
procedure TForm1.QButtonClick(Sender: TObject);
type prec=^rec;
rec=record
x,y:tp;
p,n:prec;
end;
list=record
b,e:prec;
end;
var t,bb,ee:prec;
ll,gr,ls:list;
procedure cut(var l:list;t:prec);
begin
if t^.p<>nil then t^.p^.n:=t^.n
else l.b:=t^.n;
if t^.n<>nil then t^.n^.p:=t^.p
else l.e:=t^.p;
end;
procedure clr(var l:list);
begin
l.b:=nil;
l.e:=nil;
end;
procedure add(var l:list;var t:prec);
begin
t^.n:=nil;
if l.e<>nil then l.e^.n:=t;
t^.p:=l.e;
l.e:=t;
if l.b=nil then l.b:=t;
end;
procedure con(var l1,l2:list);
begin
if l2.b<>nil then l2.b^.p:=l1.e else exit;
if l1.b<>nil then l1.e^.n:=l2.b else
begin
l1:=l2;
exit;
end;
l1.e:=l2.e;
end;
procedure proc(var ls:list;b,e:prec);
var l1,l2:list;
r,t,m:prec;
begin
if ls.b=nil then exit;
t:=ls.b;
m:=t;
while t<>nil do
begin
if (b^.x-m^.x)*(b^.y+m^.y)+(m^.x-e^.x)*(e^.y+m^.y)<(b^.x-t^.x)*(b^.y+t^.y)+(t^.x-e^.x)*(e^.y+t^.y) then
m:=t;
t:=t^.n;
end;
cut(ls,m);
clr(l1);
t:=ls.b;
while t<>nil do
begin
r:=t^.n;
if (t^.x-b^.x)*(m^.y-b^.y)>(m^.x-b^.x)*(t^.y-b^.y) then
begin
cut(ls,t);
add(l1,t)
end;
t:=r;
end;
clr(l2);
t:=ls.b;
while t<>nil do
begin
r:=t^.n;
if (t^.x-e^.x)*(m^.y-e^.y)<(m^.x-e^.x)*(t^.y-e^.y) then
begin
cut(ls,t);
add(l2,t)
end;
t:=r;
end;
con(gr,ls);
proc(l1,b,m);
proc(l2,m,e);
ls:=l1;
add(ls,m);
con(ls,l2);
end;
begin
time:=now;
kkk:=0;
repeat
while sn<>nil do
begin
tt:=sn^.n;
dispose(sn);
sn:=tt;
end;
clr(ls);
clr(gr);
tt:=cn;
if tt=nil then exit;
while tt<>nil do
begin
new(t);
t^.x:=tt^.x;
t^.y:=tt^.y;
tt:=tt^.n;
add(ls,t);
end;
bb:=ls.b;
t:=ls.b;
while t<>nil do
begin
if (t^.x<bb^.x)or((t^.x=bb^.x)and(t^.y<bb^.y))
then bb:=t;
t:=t^.n;
end;
cut(ls,bb);
t:=ls.b;
while (t<>nil) and ((t^.x=bb^.x)and(t^.y=bb^.y)) do
t:=t^.n;
ee:=t;
while t<>nil do
begin
if ((t^.x<>bb^.x)or(t^.y<>bb^.y)) and
(((t^.x-bb^.x)*(ee^.y-bb^.y)<(ee^.x-bb^.x)*(t^.y-bb^.y)) or
(((t^.x-bb^.x)*(ee^.y-bb^.y)=(ee^.x-bb^.x)*(t^.y-bb^.y))and(abs(ee^.x-bb^.x)+abs(ee^.y-bb^.y)<abs(t^.x-bb^.x)+abs(t^.x-bb^.x))))
then ee:=t;
t:=t^.n;
end;
if (ee<>nil) and ((ee^.x<>bb^.x) or (ee^.y<>bb^.y)) then
begin
cut(ls,ee);
proc(ls,bb,ee);
clr(ll);
add(ll,bb);
con(ll,ls);
add(ll,ee);
ls:=ll;
end else
begin
clr(ls);
add(ls,bb);
dispose(ee);
end;
t:=ls.b;
while ls.b<>nil do
begin
if (t=ls.b)or(t=ls.e)or
((t^.x-t^.p^.x)*(t^.n^.y-t^.p^.y)<>(t^.n^.x-t^.p^.x)*(t^.y-t^.p^.y)) then writ(t^.x,t^.y);
t:=t^.n;
dispose(ls.b);
ls.b:=t;
end;
t:=gr.b;
while t<>gr.e do
begin
t:=t^.n;
dispose(t^.p);
end;
if t<>nil then dispose(t);
inc(kkk);
until now-time>timew;
str((now-time)/kkk*24*60*60:0:6,strr);
TimeL.Caption:=strr+'s';
PaintBox1.Refresh;
end;
{------------------------------}
procedure TForm1.DiveRuleClick(Sender: TObject);
type
prec=^rec;
rec=record
a,x,y:tp;
p,n:prec;
end;
var r,t,ls,gs:prec;
procedure add(var l:prec;t:prec);
begin
if l=nil then
begin
l:=t;
t^.n:=l;
t^.p:=l
end else
begin
t^.n:=l;
t^.p:=l^.p;
l^.p^.n:=t;
l^.p:=t;
end;
end;
function arc(x,y:extended):extended;
begin
if abs(x)>abs(y) then
begin
if x>0 then
arc:=1+y/x
else
arc:=5+y/x;
end
else
begin
if y>0 then
arc:=3-x/y
else
begin
if abs(y)=0 then
arc:=0
else
arc:=7-x/y;
end;
end;
end;
procedure con(var l1,l2:prec);
var t:prec;
begin
if l2=nil then exit;
if l1=nil then
begin
l1:=l2;
exit;
end;
l1^.p^.n:=l2;
l2^.p^.n:=l1;
t:=l1^.p;
l1^.p:=l2^.p;
l2^.p:=t;
end;
procedure cut(l1,l2:prec);
var t:prec;
begin
l1^.p^.n:=l2;
l2^.p^.n:=l1;
t:=l1^.p;
l1^.p:=l2^.p;
l2^.p:=t;
end;
procedure grah(var st:prec);
var r,t,d:prec;
f:integer;
begin
if st^.n=st^.p then exit;
r:=st;
t:=st;
f:=0;
while (f<=0) or (t<>r) do
begin
if t^.n=t^.p then break;
if ((t^.n^.x-t^.p^.x)*(t^.y-t^.p^.y)>(t^.x-t^.p^.x)*(t^.n^.y-t^.p^.y))
or (((t^.n^.x-t^.p^.x)*(t^.y-t^.p^.y)=(t^.x-t^.p^.x)*(t^.n^.y-t^.p^.y))
and (abs(t^.y-t^.p^.y)+abs(t^.y-t^.n^.y)=abs(t^.p^.y-t^.n^.y)) and(abs(t^.x-t^.p^.x)+abs(t^.x-t^.n^.x)=abs(t^.p^.x-t^.n^.x)))
then
begin
if t=r then
begin
dec(f);
r:=t^.n;
end;
d:=t;
t:=t^.n;
cut(t,d);
t:=t^.p;
con(gs,d);
end else
begin
t:=t^.n;
if t=r then inc(f);
end;
end;
st:=t;
end;
procedure proc(var ls:prec);
var t,l1,l2,r,l:prec;
x,y:tp;
f:boolean;
begin
if ls^.n=ls
then exit;
l1:=ls;
l2:=ls;
repeat
l1:=l1^.n;
l2:=l2^.p;
until (l1=l2) or (l1^.p=l2);
l1:=ls;
cut(l1,l2);
proc(l1);
proc(l2);
if l1^.n=l1 then
if l2^.n<>l2 then begin
t:=l1;
l1:=l2;
l2:=t;
end else
begin
l1^.n:=l2;
l1^.p:=l2;
l2^.n:=l1;
l2^.p:=l1;
ls:=l1;
exit;
end;
x:=(l1^.x+l1^.n^.x+l1^.n^.n^.x)/3;
y:=(l1^.y+l1^.n^.y+l1^.n^.n^.y)/3;
r:=l1;
r^.a:=arc((r^.x-x),(r^.y-y));
t:=l1;
repeat
t^.a:=arc((t^.x-x),(t^.y-y));
if (r^.a>t^.a) or ((r^.a=t^.a) and (abs(r^.x-x)+abs(r^.y-y)>abs(t^.x-x)+abs(t^.y-y))) then r:=t;
t:=t^.n;
until t=l1;
l1:=r;
l:=l2;
r:=l;
t:=r;
f:=false;
repeat
if (t.x-x)*(r^.y-y)>(r^.x-x)*(t.y-y) then r:=t;
if (t.x-x)*(l^.y-y)<(l^.x-x)*(t.y-y) then l:=t;
f:=f or((x-t^.p^.x)*(t^.y-t^.p^.y)>(t^.x-t^.p^.x)*(y-t^.p^.y));
t:=t^.n;
until (t=l2);
if (l^.x=x) and (l^.y=y) then r:=r^.n
else l:=l^.n;
if f then
begin
cut(l,r);
if l<>r then con(gs,l);
end;
l2:=r;
r:=l2;
r^.a:=arc((r^.x-x),(r^.y-y));
t:=l2;
repeat
t^.a:=arc((t^.x-x),(t^.y-y));
if (r^.a>t^.a) or ((r^.a=t^.a) and (abs(r^.x-x)+abs(r^.y-y)>abs(t^.x-x)+abs(t^.y-y))) then r:=t;
t:=t^.n;
until t=l2;
l2:=r;
l1^.p^.n:=nil;
l2^.p^.n:=nil;
r:=l1;
l:=l2;
ls:=nil;
while (r<>nil) and (l<>nil) do
begin
if (r^.a<l^.a)or((r^.a=l^.a)and(abs(r^.x-x)+abs(r^.y-y)<abs(l^.x-x)+abs(l^.y-y)))then
begin
t:=r;
r:=r^.n;
if r<>nil then r^.p:=t^.p;
add(ls,t);
end else
begin
t:=l;
l:=l^.n;
if l<>nil then l^.p:=t^.p;
add(ls,t);
end;
end;
if r<>nil then
begin
r^.p^.n:=r;
con(ls,r);
end;
if l<>nil then
begin
l^.p^.n:=l;
con(ls,l);
end;
grah(ls);
end;
begin
time:=now;
kkk:=0;
repeat
while sn<>nil do
begin
tt:=sn^.n;
dispose(sn);
sn:=tt;
end;
ls:=nil;
gs:=nil;
tt:=cn;
if tt=nil then exit;
while tt<>nil do
begin
new(t);
t^.x:=tt^.x;
t^.y:=tt^.y;
tt:=tt^.n;
add(ls,t);
end;
proc(ls);
t:=ls;
if t<>nil then
repeat
r:=t;
writ(t^.x,t^.y);
t:=t^.n;
dispose(r);
until t=ls;
t:=gs;
if t<>nil then
repeat
r:=t;
t:=t^.n;
dispose(r);
until t=gs;
inc(kkk);
until now-time>timew;
str((now-time)/kkk*24*60*60:0:6,strr);
TimeL.Caption:=strr+'s';
PaintBox1.Refresh;
end;
{Div end}
procedure TForm1.CircleClick(Sender: TObject);
var
i:integer;
t:pr;
begin
while cn<>nil do
begin
t:=cn^.n;
dispose(cn);
cn:=t;
end;
while sn<>nil do
begin
t:=sn^.n;
dispose(sn);
sn:=t;
end;
mx:=0;
my:=0;
for i:=1 to QRandom.Value do
begin
new(t);
t^.n:=cn;
cn:=t;
t^.x:=Range.Value*sin(i);
t^.y:=Range.Value*cos(i);
if mx<abs(t^.x) then mx:=abs(t^.x);
if my<abs(t^.y) then my:=abs(t^.y);
end;
if mx<>0 then mx:=0.8*(Width div 2)/mx;
if my<>0 then my:=0.8*(Height div 2)/my;
PaintBox1.Refresh;
end;
{ online}
procedure TForm1.Button2Click(Sender: TObject);
label onend;
type
prec=^TTree;
TTree=record
x,y:tp;
l,r,u,n,p,gr:prec;
kl,kr:integer;
end;
var ls,t,p,n,gr:prec;
procedure disp(t:prec);
begin
if t=nil then exit;
disp(t^.l);
disp(t^.r);
dispose(t);
end;
function max(a,b:integer):integer;
begin
if a>b then max:=a
else max:=b;
end;
procedure getleft(m,n:prec;var l:prec);
var fm,fn,f:boolean;
begin
l:=nil;
if ((p^.x=m^.x) and (p^.y=m^.y)) or ((p^.x=n^.x) and (p^.y=n^.y)) then exit;
if ((p^.x=m^.n^.x) and (p^.y=m^.n^.y)) or ((p^.x=n^.n^.x) and (p^.y=n^.n^.y)) then exit;
if (m^.n=m) or
(((m^.n^.x-p^.x)*(m^.y-p^.y)=(m^.x-p^.x)*(m^.n^.y-p^.y)) and (abs(m^.x-p^.x)=abs(m^.n^.x-p^.x)+abs(m^.n^.x-m^.x)) and (abs(m^.y-p^.y)=abs(m^.n^.y-p^.y)+abs(m^.n^.y-m^.y))) or
(((m^.p^.x-p^.x)*(m^.y-p^.y)>(m^.x-p^.x)*(m^.p^.y-p^.y)) and ((m^.n^.x-p^.x)*(m^.y-p^.y)>(m^.x-p^.x)*(m^.n^.y-p^.y)))
then
begin
l:=m;
exit;
end;
if (n^.n=n) or
(((n^.n^.x-p^.x)*(n^.y-p^.y)=(n^.x-p^.x)*(n^.n^.y-p^.y)) and (abs(n^.x-p^.x)=abs(n^.n^.x-p^.x)+abs(n^.n^.x-n^.x)) and (abs(n^.y-p^.y)=abs(n^.n^.y-p^.y)+abs(n^.n^.y-n^.y))) or
(((n^.p^.x-p^.x)*(n^.y-p^.y)>(n^.x-p^.x)*(n^.p^.y-p^.y)) and ((n^.n^.x-p^.x)*(n^.y-p^.y)>(n^.x-p^.x)*(n^.n^.y-p^.y)))
then
begin
l:=n;
exit;
end;
if m^.n<>m then
begin
fm:=((m^.n^.x-p^.x)*(m^.y-p^.y)>(m^.x-p^.x)*(m^.n^.y-p^.y)) or
((m^.p^.x-p^.x)*(m^.y-p^.y)<(m^.x-p^.x)*(m^.p^.y-p^.y));
fn:=((n^.n^.x-p^.x)*(n^.y-p^.y)>(n^.x-p^.x)*(n^.n^.y-p^.y)) or
((n^.p^.x-p^.x)*(n^.y-p^.y)<(n^.x-p^.x)*(n^.p^.y-p^.y));
f:=(m^.x-p^.x)*(n^.y-p^.y)>(n^.x-p^.x)*(m^.y-p^.y);
if (m^.l<>nil) and ((f and not(fn)) or (not(f) and fm)) then
getleft(m^.l,n,l)
else if m^.r<>nil then
getleft(m^.r,m^.n,l);
end;
end;
procedure getright(m,n:prec;var l:prec);
var fm,fn,f:boolean;
begin
l:=nil;
if ((p^.x=m^.x) and (p^.y=m^.y)) or ((p^.x=n^.x) and (p^.y=n^.y)) then exit;
if ((p^.x=m^.p^.x) and (p^.y=m^.p^.y)) or ((p^.x=n^.p^.x) and (p^.y=n^.p^.y)) then exit;
if (m^.n=m) or
(((m^.p^.x-p^.x)*(m^.y-p^.y)=(m^.x-p^.x)*(m^.p^.y-p^.y)) and (abs(m^.x-p^.x)=abs(m^.p^.x-p^.x)+abs(m^.p^.x-m^.x)) and (abs(m^.y-p^.y)=abs(m^.p^.y-p^.y)+abs(m^.p^.y-m^.y))) or
(((m^.p^.x-p^.x)*(m^.y-p^.y)<(m^.x-p^.x)*(m^.p^.y-p^.y)) and ((m^.n^.x-p^.x)*(m^.y-p^.y)<(m^.x-p^.x)*(m^.n^.y-p^.y)))
then
begin
l:=m;
exit;
end;
if (n^.n=n) or
(((n^.p^.x-p^.x)*(n^.y-p^.y)=(n^.x-p^.x)*(n^.p^.y-p^.y)) and (abs(n^.x-p^.x)=abs(n^.p^.x-p^.x)+abs(n^.p^.x-n^.x)) and (abs(n^.y-p^.y)=abs(n^.p^.y-p^.y)+abs(n^.p^.y-n^.y))) or
(((n^.p^.x-p^.x)*(n^.y-p^.y)<(n^.x-p^.x)*(n^.p^.y-p^.y)) and ((n^.n^.x-p^.x)*(n^.y-p^.y)<(n^.x-p^.x)*(n^.n^.y-p^.y)))
then
begin
l:=n;
exit;
end;
if m^.n<>m then
begin
fm:=((m^.n^.x-p^.x)*(m^.y-p^.y)>(m^.x-p^.x)*(m^.n^.y-p^.y)) or
((m^.p^.x-p^.x)*(m^.y-p^.y)<(m^.x-p^.x)*(m^.p^.y-p^.y));
fn:=((n^.n^.x-p^.x)*(n^.y-p^.y)>(n^.x-p^.x)*(n^.n^.y-p^.y)) or
((n^.p^.x-p^.x)*(n^.y-p^.y)<(n^.x-p^.x)*(n^.p^.y-p^.y)); f:=(m^.x-p^.x)*(n^.y-p^.y)>(n^.x-p^.x)*(m^.y-p^.y);
if (m^.l<>nil) and ((f and not(fm)) or (not(f) and fn)) then
getright(m^.l,n,l)
else if m^.r<>nil then
getright(m^.r,m^.n,l);
end;
end;
procedure balance(m:prec;var t:prec;f:boolean);
var u,r,k,l:prec;
kr:integer;
begin
if m=nil then exit;
if m^.l<>nil then m^.kl:=max(m^.l^.kl,m^.l^.kr)+1 else m^.kl:=0;
if m^.r<>nil then m^.kr:=max(m^.r^.kl,m^.r^.kr)+1 else m^.kr:=0;
u:=m^.u;
k:=m;
if m^.kl>m^.kr+1 then
begin
k:=m^.l;
if k^.kr>k^.kl then
k:=k^.r;
if k^.u^.l=k then
k^.u^.l:=k^.l
else
k^.u^.r:=k^.l;
if k^.u^.l=k then
k^.u^.kl:=k^.kl
else
k^.u^.kr:=k^.kl;
if k^.l<>nil then k^.l^.u:=k^.u;
r:=m^.l;
kr:=m^.kl;
m^.l:=k^.r;
m^.kl:=k^.kr;
if k^.r<>nil then k^.r^.u:=m;
k^.l:=r;
k^.kl:=kr;
r^.u:=k;
k^.r:=m;
m^.u:=k;
if u<>nil then
begin
if u^.l=m then
u^.l:=k
else
u^.r:=k;
end
else t:=k;
k^.u:=u;
balance(m,t,false);
{ balance(r,t);}
end else
if m^.kr>m^.kl+1 then
begin
k:=m^.r;
if k^.kl>k^.kr then
k:=k^.l;
if k^.u^.r=k then
k^.u^.r:=k^.r
else
k^.u^.l:=k^.r;
if k^.u^.r=k then
k^.u^.kr:=k^.kr
else
k^.u^.kl:=k^.kr;
if k^.r<>nil then k^.r^.u:=k^.u;
r:=m^.r;
kr:=m^.kr;
m^.r:=k^.l;
m^.kr:=k^.kl;
if k^.l<>nil then k^.l^.u:=m;
k^.r:=r;
k^.kr:=kr;
r^.u:=k;
k^.l:=m;
m^.u:=k;
if u<>nil then
begin
if u^.l=m then
u^.l:=k
else
u^.r:=k;
end
else t:=k;
k^.u:=u;
balance(m,t,false);
end;
if f then balance(u,t,true);
end;
procedure ins(m,d:prec);
begin
if m^.r<>nil then m^.r^.u:=d;
d^.r:=m^.r;
d^.l:=nil;
d^.u:=m;
m^.r:=d;
balance(d,t,true);
end;
procedure cutl(l:prec;var dl,dr:prec);
var
r,c:prec;
begin
r:=l;
dl:=nil;
if r^.l<>nil then
begin
dl:=r^.l;
dl^.u:=nil;
r^.l:=nil;
r^.kl:=0;
end;
while r<>nil do
begin
c:=r^.u;
if c<>nil then
begin
if c^.r=r then
begin
if c^.u<>nil then
begin
if c^.u^.l=c then
begin
c^.u^.l:=r;
r^.u:=c^.u;
end
else
begin
c^.u^.r:=r;
r^.u:=c^.u;
end;
end else
begin
dr:=r;
r^.u:=nil;
end;
c^.r:=dl;
if dl<>nil then dl^.u:=c;
dl:=c;
dl^.u:=nil;
continue;
end;
end;
r:=r^.u;
end;
balance(l,dr,true);
end;
procedure cutr(r:prec;var dl,dr:prec);
var
l,c:prec;
begin
l:=r;
dr:=nil;
if l^.r<>nil then
begin
dr:=l^.r;
dr^.u:=nil;
l^.r:=nil;
end;
while l<>nil do
begin
c:=l^.u;
if c<>nil then
begin
if c^.l=l then
begin
if c^.u<>nil then
begin
if c^.u^.l=c then
begin
c^.u^.l:=l;
l^.u:=c^.u;
end
else
begin
c^.u^.r:=l;
l^.u:=c^.u;
end;
end else
begin
dl:=l;
l^.u:=nil;
end;
c^.l:=dr;
if dr<>nil then dr^.u:=c;
dr:=c;
dr^.u:=nil;
continue;
end;
end;
l:=l^.u;
end;
balance(r,dl,true);
end;
procedure add(p:prec);
var l,r,d:prec;
begin
getleft(t,n,l);
if l<>nil then
begin
getright(t,n,r);
if (n=r) or ((n^.x-r^.x)*(l^.y-r^.y)<(l^.x-r^.x)*(n^.y-r^.y)) then
begin
cutl(r,d,t);
n:=r;
cutr(l,t,d);
ins(l,p);
end else
begin
cutr(l,t,d);
balance(l^.n,d,true);
p^.l:=t;
t^.u:=p;
t:=d;
cutl(r,d,t);
p^.r:=t;
t^.u:=p;
t:=p;
p^.u:=nil;
balance(p,t,true);
end;
l^.n:=p;
p^.p:=l;
r^.p:=p;
p^.n:=r;
end;
end;
begin
kkk:=0;
time:=now;
repeat
while sn<>nil do
begin
tt:=sn^.n;
dispose(sn);
sn:=tt;
end;
ls:=nil;
gr:=nil;
tt:=cn;
if tt=nil then goto onend;
while tt<>nil do
begin
new(t);
t^.gr:=gr;
gr:=t;
t^.x:=tt^.x;
t^.y:=tt^.y;
t^.n:=ls;
ls:=t;
tt:=tt^.n;
end;
t:=ls;
ls:=ls^.n;
t^.u:=nil;
t^.l:=nil;
t^.r:=nil;
t^.n:=t;
t^.p:=t;
t^.kl:=0;
t^.kr:=0;
n:=t;
while ls<>nil do
begin
p:=ls;
ls:=ls^.n;
add(p);
end;
p:=n;
repeat
writ(p^.x,p^.y);
t:=p;
p:=p^.n;
until p=n;
while gr<>nil do
begin
p:=gr;
gr:=gr^.gr;
dispose(p);
end;
onend:
inc(kkk);
until now-time>timew;
str((now-time)/kkk*24*60*60:0:6,strr);
TimeL.Caption:=strr+'s';
PaintBox1.Refresh;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
while sn<>nil do
begin
tt:=sn^.n;
dispose(sn);
sn:=tt;
end;
while cn<>nil do
begin
tt:=cn^.n;
dispose(cn);
cn:=tt;
end;
halt;
end;
procedure TForm1.Button3Click(Sender: TObject);
var
i:integer;
t:pr;
begin
randomize();
while cn<>nil do
begin
t:=cn^.n;
dispose(cn);
cn:=t;
end;
while sn<>nil do
begin
t:=sn^.n;
dispose(sn);
sn:=t;
end;
mx:=0;
my:=0;
new(t);
t^.n:=cn;
cn:=t;
t^.x:=0;
t^.y:=10;
if mx<abs(t^.x) then mx:=abs(t^.x);
if my<abs(t^.y) then my:=abs(t^.y);
for i:=2 to QRandom.Value do
begin
new(t);
t^.n:=cn;
cn:=t;
t^.x:=i-2;
t^.y:=exp(i-2)/Range.Value;
if mx<abs(t^.x) then mx:=abs(t^.x);
if my<abs(t^.y) then my:=abs(t^.y);
end;
if mx<>0 then mx:=0.8*(Width div 2)/mx;
if my<>0 then my:=0.8*(Height div 2)/my;
PaintBox1.Refresh;
end;
end.
Литература
F. P. Preparata, M. I. Shamos, Computational geometry, Ph. D. Thesis, Dept. Of Comput. Sci., Yale Univ., 1985.
[i] S. G. Akl and G. T. Toussaint, Efficient convex hull algorithm for pattern recognition aplications, Proc. 4th Int’l Joint Conf. On Pattern Recognition, Kyoto, Japan, pp. 483-487 (1978).
[ii] A. Rosenfeld, Picture Processing by Computers, Academic Press, New York, 1969.
[iii] H. Freeman, Computer processing of line-drawing images, Comput. Surveys 6, 57-97 (1974).
[iv] P. McMullen and G. C. Shephard, Convex Polytopes and the Upper Bound Conjecture, Cambridge University Press, Cambridge, England, 1971
[v] R. L. Graham, An efficient algorithm for determining the convex hull of a finite planar set, Info, Proc. Lett. 1, 132-133 (1972).
[vi] A. M. Andrew, Another efficient algorithm for convex hulls in two dimension, Info. Proc. Lett. 9, 216-219 (1979).
[vii] M. I. Shamos, Computational geometry, Ph. D. Thesis, Dept. Of Comput. Sci., Yale Univ., 1978.
[viii] F. P. Preparata, An optimal real time algorithm for planar convex hulls, Comm. ACM 22, 402-405 (1979).