Простые методы экономической оценки инвестиций

Единовременные затраты, направляемые на покупку оборудования, строительство зданий и сооружений и т.п., в конечном счете аккумулируются в основном капитале,

текущие затраты, направляемые на создание запасов сырья, материалов, незавершенного производства и т.п., - в соста­ве оборотного капитала (формируют себестоимость продукции (услуг)). Для случая действующих производств используются приростные показатели текущих затрат.

Результаты и затраты формируют денежный поток (cash flow) - со­вокупность распределенных по отдельным интервалам рассматриваемого периода времени поступлений и выплат денежных средств, генерируемых его хозяйственной деятельностью, движение которых связано с факторами времени, риска и ликвидности.

Разность результатов и затрат формирует эффект (доход), позво­ляющий судить о том, что получит инвестор в результате реализации про­екта. Эффект можно представить в двух выражениях: как разность сово­купного результата и совокупных затрат и как разность совокупных ре­зультатов и текущих издержек. Последний вариант применяется лишь для статической оценки (за определенный период времени, чаще всего год), так как не учитывает разновременность затрат и результатов и не может быть использован в динамических моделях. В последних эффект рассчи­тывается как разность совокупных результатов, полученных за весь жиз­ненный цикл проекта, и суммарных затрат за тот же период с учетом не­равноценности денежных потоков во времени.

Эффект от реальных инвестиций представляет собой сумму прибыли и амортизации для новых предприятий (производств) и прирост прибыли и амортизации для инвестиций в действующее производство. Эта величина называется чистым денежным потоком (net cash flow).

Оценка же эффективности финансовых вложений сводится, главным образом, к оценке их реальной стоимости, обеспечивающей ожидаемую норму при­были. Существует большое количество моделей определения реальной стоимости финансовых инструментов. Этим занимаются дисциплины «Финансовые институты рынка» и «Финансовый менеджмент».

В развитых в экономическом отношении странах разработано и применяется большое количество методических материалов, касающихся расчетов экономической эффективности инвестиций. Пожалуй, наиболее распространенным документом такого рода являются рекомендации ЮНИДО (англ. UNIDO, United Nations Industrial Development Organization) - организации ООН по промышленному развитию.

Рекомендации ЮНИДО по оценке эффективности инвестиций были подготовлены большой группой известных на Западе ученых, банкиров, специалистов консалтинговых организаций. Они имели целью дать раз­вивающимся странам инструмент для повышения качества технико-экономических обоснований инвестиционных проектов и способствовать их стандартизации, что особенно важно в условиях глобализации эконо­мических отношений. Предложенный ЮНИДО подход и разработанная для его реализации компьютерная программа COMFAR (англ, computer model for reporting) были приняты многими государственными министер­ствами, банками, организациями по содействию инвестициям, универси­тетами, а также консультационными фирмами и инвесторами.

Первый отечественный документ подобного рода, ориентированный на рыночные экономические отношения и отразивший международный опыт и стандарты по технико-экономическому обоснованию инвестиционных проектов, появился лишь в 1994 г. Вторая редакция «Методических рекомендаций по оценке эффективности инвестиционных проектов» [3] вышла в свет в 2000 г.

Для упрощенной оценки экономической эффективности, когда имеются информационные ограничения по инвестиционному проекту или когда необходимо быстро оценить его эффективность на предваритель­ной стадии, рекомендуется использовать два основных показателя.

1. Норма прибыли, которая рассчитывается по формуле

N_p = ×100,

где П_t- чистая прибыль за определенный период времени (обычно за один год);

К - объем инвестиций.

2. Срок возмещения (окупаемости) инвестиций, который определяется следующим образом:

Т_ок = ×100,

При расчете данных показателей следует использовать исходные данные (объем производства, себестоимость и т.п.) за наиболее харак­терный год жизни проекта при достижении проектной мощности. Для оценки экономической привлекательности проекта рассчитанный показа­тель Np следует сопоставить с приемлемым для инвестора уровнем до­ходности (аналогично - для срока окупаемости).

Подобный подход долгие годы использовался в СССР, причем ус­ловия эффективности проектов были следующие:

³

где - нормативная норма прибыли (в зарубежной литературе - ин­декс рентабельности);

£

где – нормативный срок окупаемости.

Для отдельных отраслей эти нормативные показатели устанавливались соответствующими министерствами. Например, долгие годы для предприятий нефтяной, нефтеперерабатывающей и нефтехимической промышленности эти величины выглядели следующим образом:

=15% (En = 0,15);

= 6,7 года.

В это же время в Японии, США и других развитых странах эти показатели были другими: значительно выше для (35-50%) и ниже для (2-3 года). Рассмотренный пример показывает, что данные показатели носят весьма субъективный характер, и во многих случаях их использование можетдезориентировать инвестора.

 

4.1.3. Компаунинг.

Пусть вклад Q₀ (ден. ед.) помещен в банк, выплачивающий р % годовых.

Если процентные деньги (или, кратко, проценты), т.е. доход (прибыль) вкладчика, начисляются за каждый год (период начисления) по отношению к постоянной базе Q₀, то размер вклада (наращенная сумма) Q_t через t лет опре­деляется по формуле простых процентов:

Q_t = Q₀ = Q₀ (1 + it),

где i = р / 100 — ставка наращения.

Если проценты начисляются по последовательно изме­няющейся базе (т.е. за 2-й год по отношению к наращенной сумме Q₁ за 1-й год,..., за t -й год по отношению к наращен­ной сумме Q _t–1 за (t – 1) лет), то размер вклада (наращен­ная сумма) Q_t через t лет определяется по формуле слож­ных процентов:

Q_t = Q₀ = Q₀ (1 + i)^t,

Если проценты по вкладам начислять не один, а п раз в году при тех же р % годовых (р = const), то размер вклада (наращенная сумма) Q_t через t лет будет определяться по следующей формуле сложных[1] процентов:

Q'_t = Q₀ = Q₀ (1 + )^nt,

(при этом всегда, при любом n, Q'_t > Q_t).

Пример 1.4. Банк выдал кредит 10 млн руб. на пять лет под 12% годовых. Найти сумму долга (с процентами), ко­торую необходимо возвратить банку: Через сколько лет сумма долга удвоится по отношению к сумме кредита? Расчеты провести, применяя простые и сложные процен­ты, рассмотрев случаи ежегодного и поквартального их на­числения.

Решение. Сумма долга для i = 0,12 при ежегодном на­числении процентов составит:

• по формуле простых процентов

Q₅ = 10 × (1 + 0,12 × 5) = 16,0 (млн. / руб.);

• по формуле сложных процентов (1.5)

Q₅ = 10 × (1 + 0,12)⁵ » 17,623 (млн. руб.).

Необходимое число t лет для увеличения суммы долга в W раз (Qf/00 = N) составит:

• для простых процентов

t = (из соотношения 1 + it = N);

• для сложных процентов

t = (из соотношения[2] (1 + i)^t= N)

Таким образом, сумма долга удвоится по сравнению с суммой кредита (N = 2) через:

t = = 8,3 (лет) при наращении по формуле простых процентов;

t = = = 6,1 (лет) при наращении по формуле сложных процентов.

Если проценты начисляются поквартально, т.е. четыре раза в году (п = 4), то сумма долга Q'_t через t = 5 (лет) со­ставит

Q'_t = 10 (1 + )^4×5 = 10 × 1.03²⁰ = 18,061 (млн. руб.),

а срок удвоения долга (N=2) сократится до

t = = = = 5,9 (лет).

4.1.4. Дисконтирование.

Дисконтирование — решение задачи, обратной нараще­нию первоначальной суммы вклада (ссуды): найти перво­начальную сумму (Q₀, которую надо положить в банк под р% годовых, чтобы в конце срока получить заданную сум­му Q_t. Величину Q₀ при этом называют современной сум­мой Q_t.

Для простых процентов

Q₀= = Q_t (1 + it)^-1.

Для сложных процентов:

— при ежегодном начислении

Q₀= = Q_t (1 + i)^-i.

 

— при n начислениях в год, если p - const,

Q₀ = = Q_t (1 + )^-nt,

Числа (1 + it)^-1, (1 + i)^-t, (1 + i/n)^-nt, меньшие единицы, называются дисконтными множителями, а разность D = Q_t – Q₀ — дисконтом.

Пример 1.5. Сумма 5 млн. руб. выплачивается через три года. Определить ее современную стоимость и дисконт при ставке 12% годовых, применяя простые и сложные проценты (при ежегодном и поквартальном их начисле­нии). Какая сумма предпочтительнее: 3,5 млн. руб. сегодня или 5 млн. руб. через три года?

Решение. При i = 0,12, t = 3 современная сумма опреде­ляется:

• для простых процентов по формуле:

Q₀ = 5 (1 + 0,12 × 3)^-1 » 3,676 (млн. руб.);

• для сложных процентов:

— при ежегодном начислении по формуле:

Q₀ = 5 (1 + 0,12)^-3 » 3,559 (млн. руб.);

— при поквартальном начислении (п = 4) по формуле:

Q₀ = 5 (1 + 0,03)^-12 «3,507 (млн. руб.).

При этом дисконт D составит соответственно 5 – 3,676 = 1,324 млн. руб.;

5 – 3,559 = 1,441 млн. руб.; 5 – 3,507 = 1,493 млн. руб. Следовательно, сумма 5 млн. руб. через три года (при ставке р 12%) предпочтительнее, чем 3,5 млн. руб. сегод­ня.

 

4.1.5. Учет фактора времени при оценке экономической эффективности инвестиций.

Расчет эффективности инвестиций осуществляется за определенный период, называемый расчетным периодом (Т). Он включает в себя инвестиционный и производственный этапы цикла инвестиционного проекта. В качестве начального года расчетного периода принимается год начала финансирования работ по осуществлению инвестиционного про­екта. Конечный год расчетного периода определяется моментом завер­шения всего жизненного цикла инвестиционного проекта. Конечный год расчетного периода может также определяться нормативными сроками службы оборудования (амортизационный период) или годом, за предела­ми которого эксплуатация основного капитала экономически нецелесообразна.

Таким образом, в расчетах эффективности оперируют затратами и результатами, осуществляемыми в разные годы инвестиционного цикла. Согласно основополагающим принципам экономики разновременные за­траты и результаты неравноценны. Иными словами один рубль (или дру­гая денежная единица) сегодня значит больше, чем он же, полученный или затраченный через год. Этот факт имеет место не только из-за ин­фляции, но и вследствие того, что денежные средства, вовлеченные в хо­зяйственный оборот, приносят в условиях стабильной экономики опреде­ленный доход. Поэтому для суммирования денежных средств за какой-либо период они должны быть предварительно приведены к сопостави­мому виду, к единому моменту времени. Для этого используется коэф­фициент приведения (DF - от англ, discount factor).

Чтобы определить эффективность инвестиций в проект, нуж­но сравнить затраты с результатами за длительный срок. Но эти суммы, строго говоря, несравнимы из-за их разновременности. Рубль, которым мы располагаем в настоящее время, не равен руб­лю в ожидаемых доходах.

Для того чтобы инвестировать деньги в производство, часто приходится брать их в долг в виде ссуды (кредита). При этом пред­стоит не только вернуть долг, но еще и заплатить определенный процент от величины взятой суммы. В этих рассуждениях ничего не меняется, если вы являетесь хозяином денег и даете их взаймы банку, положив на депозитный счет, либо тем или иным путем вкладываете в производство, пусть даже свое собственное, с це­лью получения прибыли.

Пусть один инвестируемый рубль приносит годовую прибыль rкоп. Тогда спустя год мы получим (1+ г) руб. Следовательно, (1+г) руб. является стоимостью сегодняшнего рубля, если его инвестировать на 1 год. Через 2 года сегодняшний рубль еще раз вырастет на величину процентной ставки и мы получим (1+г) • (1+г) = (1+г)². Следовательно, через t лет мы будем иметь (1+г)^t, руб., т.е. цена инвестированных денег растет по формуле сложных процентов, как это происходит с банковским вкладом.

Если сегодня инвестировать сумму денег V, то через год она вырастет до V(l+r), а через t лет - до V (1+г)'. По этой модели сложных процентов возрастает сумма вкладов в банке.

Дисконтирование решает обратную задачу: приведение буду­щих денег к сегодняшнему (текущему) моменту времени.

Пусть инвестиционный проект сулит получение следующей прибыли по годам:

Чтобы привести эти разновременные будущие денежные ре­зультаты к текущему моменту времени, каждую из этих сумм нуж­но разделить соответственно на (1+ г), (1+г)² и т.д.:

Приведение любой суммы денег t-ro года (все равно - поступ­лений или платежей) к текущему моменту времени осуществляет­ся с помощью коэффициента дисконтирования К_t который равен:

где г - норма дисконта (г > 0).

Процедура приведения к конечному году расчетного периода назы­вается компаунингом или операцией вычисления сложных процентов:

FV = PV × (1 + q)^t, (1)

где PV - (от англ., present value) размер инвестиций (современная теку­щая стоимость);

q - норма дисконта или процентная ставка;

t - количество периодов, в течение которых инвестиции будут приносить доход;

FV- (от англ., future value) будущая стоимость величины P V.

Из формулы (1) видно, что чем больше количество периодов t, тем быстрее растет сложный процентный коэффициент, т. е., чем дольше действуют инвестиции, тем больше выгода. И, одновременно, чем больше ставка q, тем выше стоимость «сегодняшних» денег.

Рассмотрим следующий пример. Предположим, что Вы собираетесь разместить 1 тыс. руб. на банковском вкладе, при этом ставка по вкладам составляет 10% годовых (0=10%). Через год Вы получите доход в размере 100 руб., и на вкладе окажется 1,1 тыс. руб. Соответственно через 2 года на вкладе окажется 1,2 1 тыс. руб. и т.д.

Рассмотреть пример Фрая.

В практике оценки инвестиционных проектов чаще всего используют операцию обратную компаунингу - дисконтирование, определяя текущую стоимость по известной будущей стоимости:

РV = .

Выбор процентной ставки для дисконтирования (компаунинга) за­висит от минимально приемлемого для инвестора уровня доходности и источника финансирования инвестиций. Если инвестирование осуществ­ляется за счет собственного капитала, в качестве ставки используют пока­затель общей рентабельности для действующих производств, для новых предприятий - показатель среднеотраслевой рентабельности или банков­скую ставку по вкладам. Если источником финансирования выступают заемные средства, то применяют ставку процента по долгосрочным кре­дитам. В случае смешанных источников финансирования используется величина средневзвешенной стоимости капитала (подробнее см. в п. 3.2).

Учет фактора времени в оценке эффективности инвестиций направ­лен на преодоление главного недостатка простых методов - игнорирова­ния факта неравноценности одинаковых сумм поступлений и платежей, относящихся к разным периодам времени.

Для оценки используют следующие основные критерии:

1) чистая дисконтированная (текущая) стоимость, NPV;

2) внутренняя норма окупаемости (рентабельности), IRR;

3) коэффициент рентабельности инвестиций, BCR;

4) период возмещения (окупаемости) инвестиций, РВР.

 

1)Чистая (текущая) дисконтированная стоимость инвестиционного проекта.

Чистая дисконтированная (текущая) стоимость (NPV - от англ. net present value) определяется как разница между дисконтированными результатами проекта и дисконтированными затратами на его осуществ­ление. Она рассчитывается следующим образом:

NPV = ,

где t - конкретный год расчетного периода (изменяется от 0 до 7);

Д, - общая сумма доходов от инвестиций в год t;

К, - сумма инвестиций в год t;

а, - коэффициент приведения к расчетному году (коэффициент дис­контирования),

a_t = .

Условие эффективности по показателю NPV имеет следующий вид: NPV>0. Это означает, что дисконтированные доходы за весь расчетный период должны превышать дисконтированные инвестиционные затраты. NPV считается самым надежным показателем эффективности инвестиций, однако у него имеется ряд недостатков, и он не является единственным средством оценки спрогнозированных денежных потоков. Этот показа­тель определяет абсолютную величину отдачи от инвестиций, и, скорее всего, чем больше будут инвестиции, тем больше будет результат, следо­вательно, результаты сравнения инвестиций различных масштабов могут быть искажены.

Рассмотрим следующий пример. Имеется два варианта инвестиро­вания: К₁=20 тыс. руб., К₂=200 тыс. руб., NPV,=+10 тыс. руб., NPV₂=+25 тыс. руб.

Если в качестве критерия оценки эффективности инвестиций ис­пользовать только показатель NPV, то следует отдать предпочтение вто­рому варианту, однако на самом деле более эффективным окажется пер­вый вариант, так как отдача с единицы инвестированного капитала здесь выше.

Таким образом, основной недостаток показателя NP V заключается в том, что он носит абсолютный, а не относительный характер. Кроме это­го, величина показателя NPV мало информирует нас о том, с какого мо­мента времени инвестиции окажутся прибыльными.

 

2) Внутренняя норма окупаемости

Внутренняя норма окупаемости (IRR - от англ., internal rate of re­turn) определяется как такое значение нормы дисконта q_в при которой суммы дисконтированных доходов и дисконтированных единовременных затрат равны между собой:

= .

Очевидно, что в этом случае величина NPV равна нулю:

NPV = = 0.

 

4.2.8. Показатель рентабельности инвестиций.

Коэффициент рентабельности инвестиций (BCR или PI - от англ. к profitability index) определяется как отношение дисконтированного дохо­да и дисконтированных единовременных затрат и рассчитывается по сле­дующей формуле:

BCR = / .

 

Условие эффективности по этому показателю BCR > 1.

Данный показатель тесно связан с NPV. Так, если BCR > 1, то это означает, что сумма дисконтированных денежных доходов больше, чем сумма дисконтированных инвестиций, следовательно, NPV будет поло­жительной. Таким образом, если BCR<1, то NPV<0; если BCR=l, то NPV=0.

 

3) Внутренняя норма рентабельности инвестиционного проекта.

Расчет IRR, как правило, является итеративным процессом. Он на­чинается с приближенного задания такой нормы дисконта, при которой суммарная текущая стоимость денежных поступлений равнялась бы те­кущей стоимости осуществленных затрат. Затем рассчитывается величи­на NPVit сравнивается с нулем. Если она положительна, то в следующей итерации будет использоваться измененная на определенный шаг вели­чина д. На том шаге, когда величина NPV меняет свое значение с положительного на отрицательное (или наоборот), определяется искомое значение величины IRR. Часто при этом используется метод графической ин­терполяции (рис. 1).

Условие эффективности для показателя IRR выглядит следующим образом: IRR>q. Точное значение показателя IRR можно определить по следующей формуле:

IRR = ,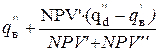

где –норма дисконта, при которой NPV принимает ближайшее нулю положительное (или отрицательное) значение;

- норма дисконта, повышенная (пониженная) на 1 пункт по срав­нению с q₀;

NPV’,NPV’’ –- величина NPV при и соответственно.

Рис. 1. Графический способ определения показателя IRR

Показатель IRR определяет для инвестора ту границу, при которой инвестиции начинают давать эффект. Обычно он сравнивается с каким-то барьерным, приемлемым для инвестора уровнем доходности (подробнее в п. 2.3.1). Кроме того, IRR часто используется для сравнения эффективно­сти альтернативных проектов.

Показатель IRR в отличие от NPV, он не дает информацию о том, сколько собст­венно дохода принесут инвестиции.

 

4) Срок окупаемости инвестиционного проекта. Период возврата (возмещения) инвестиций (РВР или РР - от

англ, payback period) определяет такой срок (t_ок), при котором суммарные дисконтированные доходы равны суммарным дисконтированным едино­временным затратам:

= .

= 0.

Значение РВР определяется суммированием нарастающим итогом денежных потоков до того момента, когда NPV будет равна нулю. Усло­вие эффективности для РВР: РВР<Т. Показатель РВР позволяет судить не только об общей эффективности или неэффективности инвестиций путем сравнения с величиной расчетного периода, но и о степени ликвидности инвестиций, т. е. определяет, за какой период распределенный во времени доход покрывает инвестиционные затраты. Это особенно важно для фирм, активно использующих заемный капитал при инвестировании, а также для фирм, имеющих нетрадиционную структуру пассивов.

Графический способ определения показателя РВР представлен на рис.2.2.

Рис. 2.2. Графический способ определения показателя РВР

 

Основным недостатком критерия РВР является то, что доходы, по­лученные за пределами рассматриваемого периода возврата, не влияют на величину срока окупаемости.

Показатель РВР активно используется в тех случаях, когда эконо­мическая ситуация является нестабильной как на макро-, так и на микро­уровне.

Проведенный выше анализ основных показателей эффективности инвестиций, учитывающих фактор времени, указывает на то, что по от­дельности использование этих критериев нецелесообразно. На практике рассчитывают и анализируют все критерии, а также проводят оценку чув­ствительности проекта (меняя основные технико-экономические показа­тели: объемы производства, цену на ресурсы и продукцию и т.д., оцени­вают те изменения, которые происходят с критериями).

 

[1] Наращенная сумма Q_t по простым процентам при p = const опреде­ляется по формуле (1.4) и не зависит от числа n начислений.

[2] Логарифмы можно брать по любому основанию; например, t = , где In N — натуральный логарифм числа N.