Проследим этапы построения поверхности в 3-х мерном пространстве.
Сначала с помощью векторов x и y задается область построения графика функции z(x,y). Диапазон значений по оси x задается вектором x, а по оси y – вектором y. Теперь с помощью команды meshgrid () на основе этих векторов надо сформировать прямоугольную сетку, являющуюся основанием для построения поверхности.
[X, Y]= meshgrid(x,у)
При этом формируются две матрицы X и Y, в которые записывается информация о координатах узлов сетки. Матрица X содержит одинаковые строки, сформированные из значений вектора x. Матрица Y содержит одинаковые столбцы, сформированные из значений вектора y. Наложение этих матриц дает координаты узлов сетки. Затем вычисляются значения функции в узлах, которые записываются в матрицу Z. Её размер будет равен произведению количества значений первого вектора на количество значений второго.
Для вычерчивания каркасных поверхностей в трехмерном пространстве существуют две основные функции: mesh и surf.
Команда mesh(Z) строит прозрачную сетчатую поверхность, а команда surf(Z) – затененную непрозрачную (сплошную) поверхность, где Z – матрица, значения элементов которой определяют соответствующие координаты на графике.
При использовании функции mesh() получается график, образованный интерполяцией точек массивов X, Y и Z линиями по осям Ox и Oy. Кроме того, цветом указывается уровень точки по оси Oz: от самого малого значения (синего) до самого большого (красного) и производится удаление «невидимых» линий. Это позволяет лучше визуально оценивать структуру трехмерного графика по сравнению с функцией plot3().
Построим поверхность (седлообразную) по формуле: z=x2-y2.
Вектор х =y = -2:0.1:2
|
|
C помощью функции meshgrid cформируем матрицы X и Y:
[X, Y]= meshgrid (x,y)
Вектора можно задать в отдельных переменных, например, x и y (x =-2: 0.1: 2; y =-2: 0.1:2;) или значения векторов указать прямо внутри команды, записав [X, Y]= meshgrid(-2:0.1:2,-2:0.1:2).
В случае, когда оба вектора одинаковые, то можно записать:
[X, Y]= meshgrid(x).
Запишем такую последовательность команд в скрипт-файл:
% Поверхность z=f(x,y)
% z=x^2-y^2
[X,Y]=meshgrid (-2:0.1:2,-2:0.1:2);
Z=X.^2-Y.^2;
Mesh(X,Y,Z)

Получаем картинку с сетчатой цветной поверхностью. Линии на разных участках графика окрашены в разные цвета. Эти цвета соответствуют значениям функции. Как уже упоминалось, по умолчанию оттенки красного цвета соответствуют большим значениям функции, а синего – меньшим.
На основе исходных векторов x и y формируются две матрицы, в которые записываются координаты узлов сетки. Матрица X содержит одинаковые строки, в которых заданы координаты X. Матрица Y содержит одинаковые столбцы, в которых заданы координаты Y. Наложение матриц X и Y позволяет получить пары (xi и yj), для которых в дальнейшем вычисляется значение функции Z. Значения функции в узлах сетки записываются в матрицу Z, размерность которой равна размерности матриц X и Y.
С использованием функции mesh графики получаются наглядными. Вместо команды mesh можно использовать команду plot3, но тогда поверхность получается менее красивой.
Можно сделать “прозрачной” каркасную поверхность (будет видна задняя стенка), отобразив ее скрытые части, применив команду hidden off. Отмена – hidden on.
[X,Y]=meshgrid (-2:0.1:2,-2:0.1:2);
Z=X.^2-Y.^2;
Figure(1)
Mesh(X,Y,Z)
Figure(2)
Mesh(X,Y,Z)
|
|
hidden off % делает прозрачной поверхность
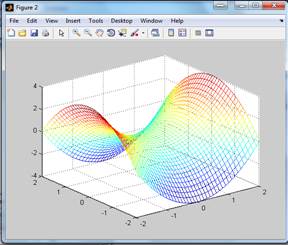
Можно использовать команду surf, и тогда картинка еще более красочная.
[X,Y]=meshgrid (-2:0.1:2,-2:0.1:2);
Z=X.^2-Y.^2;
Surf(X,Y,Z)

Для дополнительного оформления трёхмерных графиков можно использовать функции meshz и meshc, а также функцию surfc. Использование функции meshz позволяет построить " график с пьедесталом или, как еще говорят, с подложкой". Функции с суффиксом c помимо трёхмерного графика строят ещё и линии уровня (линии под графиком). График с функцией meshz ( с подложкой )

В системе ML существуют множество вариантов настройки графиков. Они могут выполняться с помощью опций интерфейса, либо с помощью команд. Все трехмерные графики, которые мы строили, можно было видеть только из одной точки обзора, т.е. позиции, с которой мы видим трехмерное изображение.
В ML можно изменять точку обзора. Эта точка характеризуется двумя параметрами: азимутом (Az) и углом возвышения (El). Азимут определяет угол поворота вокруг оси z и отсчитывается от оси, противоположной y, в направлении против часовой стрелки. Угол возвышения – это угол между отрезком, направленным из начала координат в точку обзора, и плоскостью xOy.
Когда выполняются функции mesh или surf, то по умолчанию устанавливаются значения az = -37.5°, el = 30°.
Точку обзора можно менять командой view (Az,El) или, что более просто, используя специальную кнопку на панели инструментов графического окна Figure – Rotate 3D.
Например, выведем нашу поверхность в 2-х вертикальных окнах с разными значениями азимутального угла и угла возвышения (полярного).
[X,Y]=meshgrid (-2:0.1:2,-2:0.1:2);
|
|
Z=X.^2-Y.^2;
subplot(2,1,1);
surf(X,Y,Z);
view([0 30]);
title('угол 0-30')
subplot(2,1,2);
surf(X,Y,Z);
view([60 40]);
title('угол 60-40')
