Лекция 2. Интерференция световых волн
План лекции
2.1. Когерентность и монохроматичность световых волн.
2.2. Интерференция от двух когерентных источников.
2.3. Интерференция в тонких пленках.
2.4. Интерферометры.
2.5. Использование лазерной интерферометрии в строительстве.
Когерентность и монохроматичность световых волн
Явление интерференции света состоит в перераспределении светового потока, возникающем при сложении когерентных волн и проявляющемся во взаимном усилении световых волн в одних точках пространства и ослаблении их - в других. Это приводит к появлению устойчивой картины чередующихся максимумов и минимумов интенсивности света.
Необходимым условием интерференции волн является их когерентность, т.е. согласованное протекание во времени и пространстве волновых процессов. Этому удовлетворяют монохроматические волны, для которых
.
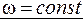Они соответствуют неограниченной в пространстве синусоидальной волне:
.
При суперпозиции (наложении) таких волн
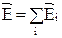
и наблюдается интерференционная картина.
Вид интерференционной картины зависит от характера наложения когерентных волн (рис. 2.1 – 2.3):
1) при таком наложении волн нет усиления сигнала:
 |
Рис. 2.1
2) при таком наложении волн имеет место равномерная освещенность экрана:
 |
Рис. 2.2
3) при таком наложении волн имеет место усиление сигнала:
 |
Рис. 2.3
Для получения когерентных волн, дающих интерференционную картину, необходимо выполнение следующих условий:
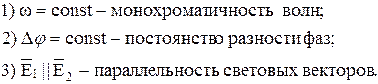
Волны монохроматичны, если:
|
|
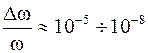
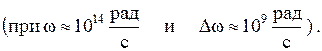
Реальные тепловые источники света дают некогерентные волны, т.к. атомы этих источников излучают свет очень короткое и конечное время:
.
Такое прерывистое излучение света атомами дает волновые цуги (см. рис. 2.4).
Рис. 2.4
Средняя продолжительность одного цуга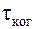 
называется временем когерентности. Длина цуга в вакууме l ц, т.е. длина когерентности, будет равна:
,
где c – скорость света в вакууме.
Сравнение источников света по степени когерентности дано в таблице 2.
Таблица 2
| Вид источника света |
|
|
|
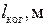
| Тепловые источники |
|
| |
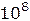
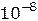
| Лазеры |
|
|
|
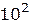
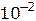
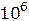
Из таблицы видно, что лазеры дают световую волну гораздо более высокой степени когерентности, чем тепловые источники света.
Для получения когерентных световых пучков от тепловых источников света применяют различные приемы: метод щелей Юнга1 (рис. 2.5), зеркала Френеля (рис. 2.6), бипризму Френеля (рис. 2.7) и другие.
Рис. 2.5
[1] Т. Юнг (1773–1829), английский ученый.
Рис. 2.6
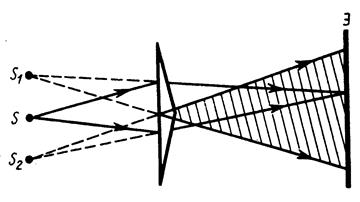
Рис. 2.7
Интерференция от двух когерентных источников
Рассчитаем интерференционную картину от двух когерентных источников (например, от двух щелей Юнга), расположенных достаточно близко друг от друга. Пусть щели S 1 и S 2 находятся на расстоянии d друг от друга (см. рис. 2.8). Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l >> d. Пусть начало отсчета находится в точке О, симметричной относительно щелей.
|
|
Интенсивность в любой точке А экрана, лежащей на расстоянии x от О, определяется оптической разностью хода Δ = r 2 n 2 - r 1 n 1. Это следует из рассмотрения сложения световых волн, излучаемых источниками S 1 и S 2.
Источник S 1 излучает световую волну:
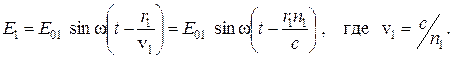
Аналогично источник S 2 излучает световую волну:
 |
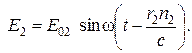
Рис. 2.8
Сложение этих двух волн при условии E 01 = E 02дает следующий результат:
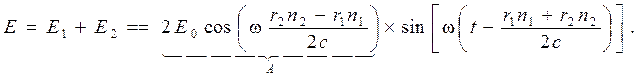
Тогда интенсивность света I, пропорциональная квадрату амплитуды A (I ~ A 2), будет равна
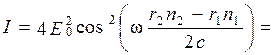
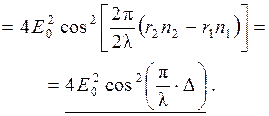
Здесь учтено, что
и, как указывалось выше, величина
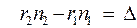
есть оптическая разность хода.
Т. к. результирующая интенсивность пропорциональна квадрату косинуса, то возможны два случая ее существования:
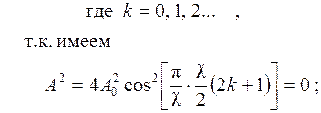
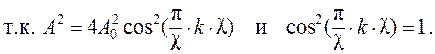
Следовательно,
условие интерференционных min: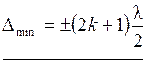 
и условие интерференционныхmax: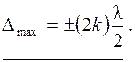 
Здесь k = 0,1,2…– порядок интерференционного максимума.
Определим положение максимумов интерференционной картины на экране. Сначала найдем
.
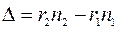Полагая n 2 = n 1 = 1, найдем разность (r 2 – r 1). Из вышеприведенного рисунка 2.8 следует:
.
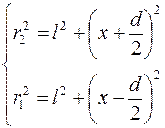Отсюда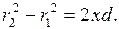 
Следовательно, положение максимумов на экране определяется при:
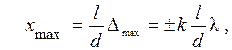
а положение минимумов при:
Здесь, по-прежнему, k = 0,1,2….
Тогда ширина интерференционной полосы (т.е. расстояние между двумя соседними максимумами) будет:
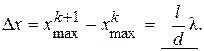
Таким образом, ширина интерференционной полосы будет зависеть от длины волны λ.
|
|