Определение вероятности. Классическое и Геометрическое.

Функция Р (А), аргументом которой являются события, а значениями - действительные числа, называется вероятностью, если выполнены следующие условия: 1) для любого события А, на котором определена вероятность; 2) 3) если то 4) если , вероятность - определена при любом n и то Четвертое условие называется аксиомой непрерывности. Смысл его состоит в том, что если аргумент функции Р (А) стремится к невозможному событию, то и значение функции стремится к нулю. Заметим, что функция Р (А) не обязательно определена для любого . Вообще у понятия вероятности много общего с понятием площади множества А. Но ведь площадь можно определить тоже не для любого множества А. Из условий 1) - 4), которым удовлетворяет вероятность, можно вывести следующие свойства:1. Действительно, и Поэтому Значит 2. Так как события А и несовместны, то

Кроме того, , и . Поэтому 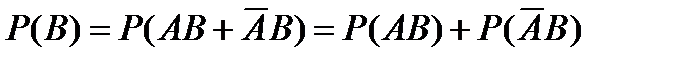и, значит, Следовательно, Перестановками называются комбинации, состоящие из одних и тех же n различных элементов, отличающиеся друг от друга только порядком расположения этих элементов. Обозначим количество различных перестановок из n элементов P _n. Согласно правилу произведение т.е. !. Размещениями называются комбинации, составленные из n различных элементов по m элементов в комбинации. Комбинации отличаются друг от друга составом элементов или их расположением. Количество размещений из n элементов по m обозначается и согласно правилу произведения Сочетаниями называются комбинации, составленные из n различных элементов, причем каждая комбинация содержит m различных элементов. Комбинации отличаются лишь составом элементов. Их расположение роли не играет. Количество сочетаний из n элементов по m обозначается . Легко понять, что в m! раз меньше, чем , т.е. . При решении комбинаторных задач нужно четко представлять, что существует способов, чтобы из совокупности n различныхэлементов извлечь без возвращения m штук (выбор без возвращения - это такой способ отбора элементов, при котором выбранный элемент не возвращается в исходную совокупность элементов).Исходя из этого легко заметить, что , т.к. выбрать m элементов из n все равно, что решить вопрос, какие n - m элементов оставить в совокупности. К лассическое определение вероятности. Оно применимо только в том случае, когда пространство элементарных исходов конечно, причем все исходы w₁,..., w_n равновозможны. Такая ситуация возникает, например, в опыте с бросанием правильной игральной кости или симметричной монеты.

Пусть А некоторое событие, причем Определим Р (А) как отношение числа исходов, благоприятствующих событию А к общему числу исходов, т.е. Р (А) = m / n. Легко проверить, что условия 1) - 3), которым должна удовлетворять вероятность, выполнены. Условие 4) проверять не надо, т.к. бесконечной последовательности в данной ситуации не существует. Геометрическое определение вероятности возникает в том случае, когда пространство элементарных исходов - есть некоторое множество на плоскости (на прямой, в пространстве), имеющее ненулевую площадь (длину, объем). Пусть А - подмножество , также имеющее площадь. Предположим, что в наугад выбирается точка. Наугад означает, что ни у какой точки нет преимущества перед другой быть выбранной. Как определить вероятность того, что точка попадает в подмножество А? Если обозначить это событие той же буквой А, то вероятность события А определяется как отношение площадей А и , т.е. Можно проверить, что условия 1) - 4) выполнены, т.е. определение вероятности введено корректно.

Два человека договорились о встрече в условленном месте между 12 и 13 часами. Каждый из них ожидает другого 15 минут. Какова вероятность, что встреча произойдет, если время прихода каждого случайно в указанном промежутке? ·Пусть x - время прихода первого, y - второго. За пространство элементарных исходов примем множество пар (x, y), удовлетворяющих условиям x£y, В системе координат x y множество точек, удовлетворяющих этим условиям, образуют треугольник АВС. Для того, чтобы встреча состоялась, необходимо и достаточно выполнение условия

3.Теорема сложения вероятностей, умножения. Условная вероятность. Независимые события.). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий. Следствие 1: Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице. Определение. Противоположными называются два несовместных события, образующие полную группу. Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления. Следствие 2: Сумма вероятностей противоположных событий равна единице.

Условная вероятность. Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало четное число очков?

В данном случае пространство элементарных исходов состоит из трех равновозможных элементарных исходов: Ω = {4, 5, 6}, и событию A = {выпало четное число очков} благоприятствуют 2 из них: A = {4, 6}. Поэтому P(A) = 2/3.

Условной вероятностью события А, при условии, что произошло событие В, называется число. Будем считать, что условная вероятность определена только в случае, когда P(В) >0. Следующее свойство называется "теоремой умножения": P(A∩B) = P(B)P(A\B) = P(A)P(B\A), если соответствующие условные вероятности определены (то есть если P(В) > 0, P(A) > 0). Теорема умножения для большего числа событий: P(A₁ ∩ A₂ ∩…∩ A_n) = P(A₁) P(A₂\A₁) P(A₃ \A₁ ∩A₂)… P(A_n \A₁∩…∩A_n-1) если соответствующие условные вероятности определены. События A и B называются независимыми, если P(A∩B) = P(A)P(B.)

4.Формула полной вероятности. Формула Бейса. Есть 3 завода, производящих одну и ту же продукцию. При этом 1-й завод производит 25%, 2-й завод — 35% и 3-й завод — 40% всей производимой продукции. Брак составляет 5% от продукции 1-го завода, 3% от продукции 2-го и 4% от продукции 3-го завода. Вся продукция смешивается и поступает в продажу. Найти а) вероятность купить бракованное изделие; б) условную вероятность того, что купленное изделие изготовлено 1-м заводом, если это изделие бракованное. Первая вероятность равна доле бракованных изделий в объеме всей продукции, то есть 0,05*0,25 + 0,03*0,35 + 0,04*0,4. Вторая вероятность равна доле брака 1-го завода среди всего брака, то есть, Определение: Набор попарно несовместных событий Н₁, Н₂… таких, что P(А_i) > 0 для всех i и

называется полной группой событий или разбиение пространства Ω. События Н₁, Н₂ …, образующие полную группу событий, часто называют гипотезами. При подходящем выборе гипотез для произвольного события А могут быть сравнительно просто вычислены P(А/ Н_i) (вероятность событию А произойти при выполнении «гипотезы» Н_i) и собственно P(Н_i) (вероятность выполнения «гипотезы» Н_i). Теорема (Формула полной вероятности).Пусть Н₁, Н₂ — полная группа событий. Тогда вероятность любого события A может быть вычислена по формуле:

Теорема (Формула Байеса).

Пусть Н₁, Н₂ …— полная группа событий и A — некоторое событие положительной вероятности. Тогда условная вероятность того, что имело место событие Н_k, если в результате эксперимента наблюдалось событие A, может быть вычислена по формуле:

Пример. Вернемся к примеру 15. Изделие выбирается наудачу из всей произведенной продукции. Рассмотрим три гипотезы: Н_i = {изделие изготовлено i -м заводом }, i = 1, 2, 3. Вероятности этих событий даны: P(Н₁) = 0,25, P(Н₂) = 0,35, P(Н₃) = 0,4. Пусть A = {изделие оказалось бракованным }. Даны также условные вероятности P(A\Н₁) = 0,05, P(A\Н₂) = 0,03, P(A\Н₃) = 0,04.

5.Независимые испытания. Формула Бернулли. Определение. Событие А называется независимым от события В, вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Предположим, что некоторый опыт проводится при неизменных условиях n раз. В результате каждого опыта может с вероятностью Р, 0 < P < 1 произойти событие А. Какова вероятность, что событие появится точно m раз, где m - целое, ? Обозначим искомую вероятность Р_n (m). Мы докажем, что имеет место следующая формула Бернулли: Обозначим через В_m сложное событие, состоящее в том, что в n опытах событие А произошло точно m раз. Запись 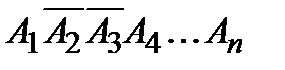будет означать, что в первом опыте событие А произошло, во втором и третьем - не произошло и т.п. Так как опыты проводятся при неизменных условиях, то Событие В_m можно представить в виде суммы всевозможных событий указанного вида, причем в каждом слагаемом буква А без черты встречается точно m раз. Слагаемые в этой сумме несовместны и вероятность каждого слагаемого равна Чтобы подсчитать количество слагаемых, заметим, что их столько, сколько есть способов для выбора m мест для буквы А без черты. Но m мест из n для буквы А можно выбрать способами. Следовательно, Пример. Наблюдения показывают, что в среднем каждый третий лебедь не возвращается в родные северные края после зимних странствий. Предположим, что благополучный перелет для каждого лебедя является независимым от других лебедей случайным событием. Осенью орнитологи сумели зарегистрировать каждую особь в большом количестве лебединых стай. Каждая такая стая состояла всего из семи лебедей. Какая, примерно, доля этих стай вернется весной в места гнездований в полном составе? Вероятность гибели в пути каждого лебедя Р = 1/3. По формуле Бернулли можно подсчитать вероятность того, что в пути из семи лебедей не погибнет ни один: .