Рассмотрим случай, когда два параметра П1 и П2 входят в состав коэффициентов характеристического полинома линейно. тогда
D(p) = D0(p) + П1D1(p) + П2D2(p) = 0.
Определим значения П1 и П2, при которых уравнение имеет пару чисто мнимых корней рi,i+1=±jωi. Для этого подставим р=jωi,- в уравнение, получим:
D(jωi) = П1D1(jωi) + П2D2 (jωi) + D0(jωi) = 0.
Это уравнение распадается на два:
П2Р1(ωi)+П1Q1(ωi)=-R1(ωi)
П2Р2(ωi)+П1Q2(ωi)=-R2(ωi)
Заметим, что в полученных уравнениях первыми стоят члены с параметром П2, и именно этот параметр должен откладываться по горизонтальной оси.

Буквами Р, Q, R обозначены вещественные и мнимые составляющие многочленов D1(jωi), D2(jωi), D0(jωi)

Решив систему относительно П2 и П1 по правилу Крамера, получим:

Параметры П2 и П1 найдены при ωi. Приняв -∞<ω<+∞, получим кривые D-разбиения в плоскости параметров П2 и П1.
определители ∆, ∆2, ∆1 являются нечетными функциями от ω, то есть:
∆(ω) =-∆(-ω); ∆2(ω) =-∆2(-ω); ∆1(ω) =-∆1(-ω);
а параметры П2 и П1 являются четными, то есть
П2(ω) =П2(-ω), П1(ω) =П1(-ω),
Это означает, что при некоторых значениях П2, и П1, взятых на границе D-разбиения, характеристическое уравнение обязательно будет иметь два комплексно-сопряженных корня рi,i+1=±jωi, расположенных на мнимой оси. Следовательно, и в плоскости параметров П2 и П1 границы областей D-разбиения являются отображениями мнимой оси плоскости корней. при изменении 0<ω<+∞, кривая D-разбиения пойдет по тем же точкам, что и при изменении -∞<ω<0,, то есть в плоскости (П2, П1) граница должна прочерчиваться дважды. Это дает возможность рассматривать значения ω только на одной полуоси jω.
При решении системы главный определитель ∆ может обратиться в нуль. При этом возможны два случая:
1) ∆ = О, ∆2≠0, ∆1≠0, тогда П2 и П1 обращаются в бесконечность и интереса не представляют;
2) ∆ = О, ∆2=0, ∆1=0, тогда П2 и П1 становятся неопределенными. ТОГДА

При этом одно уравнение системы является следствием другого и вместо двух уравнений можно рассматривать одно,

Последнее уравнение определяет положение линии, называемой особой прямой. Чтобы найти особые прямые, надо определить все значения ω, при которых ∆ = О, ∆2=0, ∆1=0
при ω = 0 получаем одно уравнение
U(0) = аn = 0.
Уравнение также является уравнением особой прямой и оно имеет математический или физический смысл, если аn(П1,П2)=0.
Также особой прямой является прямая при ω=+∞. параметры П2 и П1 являются неопределенными  , причем эти соотношения можно привести к неопределенности вида
, причем эти соотношения можно привести к неопределенности вида  , если в уравнении сделать замену p=1/q. получается
, если в уравнении сделать замену p=1/q. получается
D(q) = anqn + an-1qn-1 + …+ а0= 0
а0 стал свободным членом нового уравнения.
условию р=∞ соответствует условие q=0 и поэтому уравнением второй особой прямой будет равенство
p0(П2, П1)=0
Штриховка границ областей D-разбиения
После построения границ областей D-разбиения и особых прямых необходимо определить область, соответствующую минимальному количеству корней в правой полуплоскости. С этой целью производится штриховка границ D-разбиения и особых прямых. соответствие устанавливается с помощью правила штриховки кривых D-разбиения:
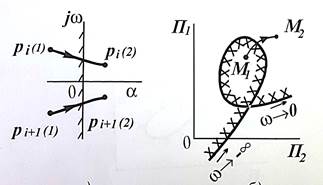
если рассматривать переход точки через границу D-разбиения со стороны двойной штриховки (из М1 в положение M2), то это будет соответствовать переходу пары корней в правую полуплоскость.
Особые прямые также должны быть заштрихованы.
Если ∆меняет знак, то направление двойной штриховки кривой D-разбиения и особой прямой изменяется. Причем особая прямая в этом случае имеет двойную штриховку.
Если особая прямая проводится при ω=∞ то она имеет одинарную штриховку, обращенную в сторону штриховки кривой D-разбиения. После пересечения с кривой D-разбиения направление штриховки особой прямой изменяется и далее остается неизменным


Заштрихованные по изложенным правилам границы направлением своей штриховки указывают на области, имеющие наименьшее количество корней в правой полуплоскости. Чтобы убедиться, что претендующая область в действительности является областью устойчивости, необходимо для одной точки внутри этой области сделать строгую проверку устойчивости по известным математическим критериям.
легко найти количество корней в правой полуплоскости для всех остальных областей. Для этого достаточно передвигать изображающую точку из одной области в другую и увеличивать количество корней в правой полуплоскости на два, если эта точка пересекает границу со стороны двойной штриховки или на один корень, если пересекается особая прямая со стороны одинарной штриховки.