Исходные данные заносятся в таблицу размерности (n+1) × (n+1). Если дуга  , то в соответствующей клетке таблицы записывается значение dij.
, то в соответствующей клетке таблицы записывается значение dij.
Если обратная дуга  , то в соответствующей клетке записывается значение dji, если дуга
, то в соответствующей клетке записывается значение dji, если дуга  , то в клетке (j,i) записывается Ø.
, то в клетке (j,i) записывается Ø.
Если дуги  ,
, 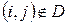 , то соответствующие клетки остаются пустыми. Итак, заполненными будут только клетки, симметричные относительно главной диагонали.
, то соответствующие клетки остаются пустыми. Итак, заполненными будут только клетки, симметричные относительно главной диагонали.
*
| j i | Ll00000 0 | … | … | … | n |
| … | d0j | … | d0n | ||

|

| ||||
| i | di0 | … | dij | … | din |

|

| ||||
| n | dn0 | … | dnj | … |
Каждый шаг алгоритма Форда состоит из трёх действий.
1.Находится путь по таблице из узла- истока Ø в узел-сток n с пропускной способностью больше 0. Для этого столбец, соответствующий узлу-истоку, отмечается знаком *. Далее отыскиваются в строке с номером 0 элементы dij > 0 и столбцы, в которых они находятся, отмечаются сверху номером просматриваемой строки (цифрой 0). В результате окажутся выделенными все дуги (0, j) c положительными пропускными способностями. Эти дуги могут служить первыми дугами пути из истока в сток.
Далее просматриваются те строки, номера которых совпадают с номерами отмеченных столбцов. В каждой такой строке i отыскиваются элементы dij > 0, находящиеся в непомеченных столбцах, и эти столбцы отмечаются номером просматриваемой строки. Таким образом, окажутся выделенными дуги, которые могут служить вторыми дугами путей из истока в сток.
Аналогичный просмотр строк продолжается до тех пор, пока: а) либо не будет помечен столбец с номером n (сток) что означает выделение пути с пропускной способностью больше нуля из истока в сток; б) либо нельзя помечать новые столбцы (в просматриваемых строках не окажется положительных элементов), при этом столбец с номером n также останется не отмеченным.
|
|
В последнем случае отсутствует путь из источника в сток, проходящий по дугам с положительной пропускной способностью.
В случае ” а ” искомый путь µ из источника в сток находится используя пометки столбцов. Пусть последний столбец n помечен номером k, тогда дуга (k,n) последнее звено искомого пути. Далее просматривается столбец с номером k, пусть отметка этого столбца l. Тогда дуга (l,k) предпоследнее звено искомого пути и т.д.Этот процесс продолжается до тех пор, пока не найдётся отметка *, т.е. отметка истока Ø. Пусть эта отметка будет цифра m. Таким образом путь от истока к стоку будет состоять из дуг µ =((Ø, m),…, (l,k), (k,n)). (5)
2.Клетки, соответствующие дугам этого пути, отмечаются знаком (–), а симметричные им клетки, т.е. соответствующие обратным дугам – знаком (+). По найденному пути (5) можно пропустить максимально возможный поток, величина которого равна Θ = min { dij- }.Эта величина Θ отнимается от всех пропускных способностей клеток, отмеченных знаком (–) и прибавляется к пропускным способностям клеток, отмеченных знаком (+). В результате получается новая таблица, в которой записаны неиспользованные пропускные способности дуг после пропускания максимального потока по пути (5).
По новой таблице опять отыскивается, уже другой, путь от истока к стоку, состоящий из дуг с неиспользованными пропускными способностями. Если такой путь существует, то по этому пути пропускается максимально возможный поток из истока в сток. После этого корректируется таблица аналогично как на этапе 1.
|
|
Это процесс продолжается до тех пор, пока не будет иметь место случай б).
3.Пусть имеется случай б), т.е. когда не существует пути из истока в сток, состоящий из дуг с неиспользованными пропускными способностями. Это означает, что найдены все возможные пути перевозки продукции и задача решена. Для определения максимального потока на сети V* в последней таблице выделяются отмеченные столбцы, номера которых образуют множество R*, причём исток  *. В результате получается минимальный разрез (R *,
*. В результате получается минимальный разрез (R *, 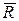 *) и по теореме Форда- Фалкерсона
*) и по теореме Форда- Фалкерсона

Для нахождения значений потоков по дугам xij*, образующих поток V* из элементов первой таблицы вычитаются соответствующие элементы последней таблицы. Если в клетке получается неотрицательная величина, то она оставляется; если – отрицательная, то в клетке записывается  . Значения заполненных клеток будут соответствовать потокам по дугам xij*. Причём
. Значения заполненных клеток будут соответствовать потокам по дугам xij*. Причём

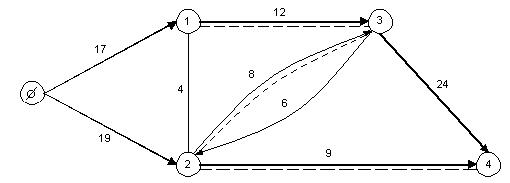
Пример. На данной сети определить максимальный поток из узла  в узел 4.
в узел 4.
1. * 0 0 1 2
| i j | |||||
| 0+ | 19- 0+ | 9- |
Θ1 = min (19,9)=9.
2. * 0 0 1 3
| i j | |||||
| 0+ | 17- 0+ | 10 9 | 12- 0+ | 24- |
Θ2 = min (17,12,24)=12.
3. * 0 0 2 3
| i j | |||||
| 12 9+ | 5 | 10- 6+ 9 | 8- 12 | 12- |
Θ3 = min (10,8,12)=8.
4. * 0 0 1 2
| i j | |||||
| 12 17 | 5 12 | 2 14 9 | 12 | 4 |
Пути из 0 в 4 нет! Определяются множества: R*={0,1,2},  ={3,4}.
={3,4}.
|
|
(R *, 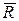 *)=((1,3),(2,3),(2,4))
*)=((1,3),(2,3),(2,4))
d (R *, 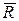 *)= V* =12+8+9=29
*)= V* =12+8+9=29
5. В заключительной таблице положительные элементы определяют потоки по дугам xij*.
| i j | |||||
| -12 -17 | 12 | 17 -8 -9 | 12 -12 | 9 20 |