Цель работы
Целью работы является изучение вопросов синтеза надежной конфигурации систем распределенной обработки данных.
Общие теоретические сведения
Введение
Задача проектирования системы распределенной обработки данных заданной надежности формулируется чаще всего следующим образом.
Дано: топология исходной системы распределенной обработки данных, набор резервных линий, надежность каждого из исходных и резервных элементов, стоимость каждой из резервных линий.
Минимизировать: суммарную стоимость введенных резервных линий.
Варьируются: топологические варианты введения резервных линий.
Ограничение: надежность синтезированного варианта топологии не менее заданной.
Физическая и математическая модели систем распределенной обработки данных
Физической моделью систем распределенной обработки данных можно считать совокупность узлов, некоторые из которых соединены линиями связи. Чаще всего оказывается допустимым считать узлы системы абсолютно надежными, так как их надежность многократно превышает надежность линий.
Поток отказов линий связи можно описать процессом восстановления с конечным временем восстановления.
Поток отказов линий связи допустимо описывать экспоненциальными законами распределений.
Опишем математическую модель системы распределенной обработки данных.
Абсолютно надежным узлам физической модели соответствуют вершины случайного графа, пронумерованные натуральными числами от 1 до n. Линиям связи физической модели соответствуют ребра графа, вершины графа абсолютно "надежны", а каждое из его ребер r "отказывает" и "восстанавливается" в соответствии с экспоненциальными законами распределений времен безотказной работы и восстановления имитируемых линий связи. Ребра ведут себя независимо.
Матричный метод вычисления вероятности связности случайного графа
Пусть G - случайный, неориентированный граф без петель, сопоставлен системе распределенной обработки данных, для которой необходимо определить вероятность того, что в произвольный момент времени между любой парой узлов системы существует хотя бы один путь, т.е. вычислить вероятность P(G) связности графа G. Пусть n - число вершин графа, а сами вершины пронумерованы натуральными числами от 1 до n. Символы [i,j] будем обозначать ребро G, соединяющее вершины "i" и "j". Пусть qij - вероятность отказа ребра [i,j] (при i=j, qij=0, что соответствует предположению об абсолютной надежности узлов системы).
Будем считать, что G - полный граф. В этом случае ребра графа, не имеющие аналогов - линий связи, характеризуются qij=1. Каждый такой граф полностью определяется симметрической матрицей (qij), у которой на главной диагонали стоят нули, а на месте i,j - вероятность отказа ребра [i,j]. Вероятность P(G) связности такого графа является функцией матрицы смежности (qij). Обозначая эту функцию через Pn((qij)), запишем:
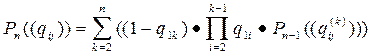 , (1)
, (1)
где 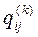 - симметрические матрицы,
- симметрические матрицы,
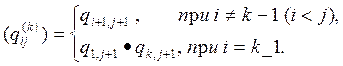
Упрощает пользование методом следующее пояснение:
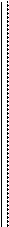
 0 q1,2 q1,3... q1,k+1 q1,k+2... q1,n
0 q1,2 q1,3... q1,k+1 q1,k+2... q1,n
0 q2,3...................................
если (qij)= 0 qk,k+1 qk,k+2... qk,n,
...................................
0 qn-1,n
то 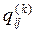 получается из (qij), если каждый обведенный элемент k строки умножить на лежащий над ним элемент первой строки, а после этого вычеркнуть из (q 4ij 0) первую строку и первый столбец.
получается из (qij), если каждый обведенный элемент k строки умножить на лежащий над ним элемент первой строки, а после этого вычеркнуть из (q 4ij 0) первую строку и первый столбец.
Пример. Вычислим вероятность связности полного графа G на пяти вершинах при условии, что все его ребра отказывают с одной и той же вероятностью "q", т.е. графу G соответствует матрица
 0 q q q q
0 q q q q
0 q q q
Q = 0 q q
0 q
В соответствии с (1) на первом шаге получаем:
P(G)=(1-q) [P(Q1) + qP(Q2) + q2P(Q3) + q3P(Q4)],
где
0 q2 q2 q2 0 q q q
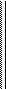
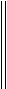 Q1 = 0 q q; Q2 = 0 q2 q2 ;
Q1 = 0 q q; Q2 = 0 q2 q2 ;
0 q 0 q
0 0
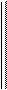
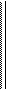
 0 q q q 0 q q q
0 q q q 0 q q q
Q3 = 0 q q; Q4 = 0 q q..
0 q2 0 q
0 0
На втором шаге:
P(Q1) = (1-q2)[P(Q5) + q2P(Q6) + q4P(Q7)],
P(Q2) = (1-q)[P(Q5) + qP(Q8) + q2P(Q9)],
P(Q3) = (1-q)[P(Q8) + qP(Q6) + q2P(Q10)],
P(Q4) = (1-q)[P(Q9) + qP(Q10) + q2P(Q7)],
где
 0 q3 q3 0 q q3 0 q q
0 q3 q3 0 q q3 0 q q
Q5 = 0 q; Q6 = 0 q3; Q7 = 0 q;
0 0 0
 0 q2 q2 0 q2 q2 0 q q
0 q2 q2 0 q2 q2 0 q q
Q8 = 0 q2; Q9 = 0 q; Q10 = 0 q2.
0 0 0
На третьем шаге:
P(Q5) = (1-q3)[P(Q11) + q3P(Q12)],
P(Q6) = (1-q)[P(Q11) + qP(Q13)],
P(Q7) = (1-q)[P(Q14) + qP(Q12)],
P(Q8) = (1-q2)[P(Q11) + q2P(Q14)],
P(Q9) = (1-q2)[P(Q13) + q2P(Q12)],
P(Q10) = (1-q)[P(Q13) + qP(Q14)],
где
Q11 = 0 q4 à P(Q11) = 1 - q4;
 0
0
 Q12 = 0 q à P(Q12) = 1 - q4;
Q12 = 0 q à P(Q12) = 1 - q4;
 Q13 = 0 q3 à P(Q13) = 1 - q3;
Q13 = 0 q3 à P(Q13) = 1 - q3;
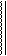 Q14 = 0 q2 à P(Q14) = 1 - q2.
Q14 = 0 q2 à P(Q14) = 1 - q2.
Результат удобно записать, пользуясь обозначением Sk = (1 - qk), в виде
P(G) = S1S2S3S4 + q(S1)2S3S4 + 3q2(S1)2S2S4 + q3[4(S1)2S2S3 + + (S1)3S4] + q4[3(S1)2(S2)2 + 3(S1)3S3)] + 6q5(S1)3S2 + q6(S1)4.