МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Курганский государственный университет
Кафедра автоматизации производственных процессов
ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ
Методические указания к
выполнению контрольного задания
по курсам “Теория автоматического управления”,
“Управление техническими системами”
для студентов специальностей 210200, 030500, 330100
заочной формы обучения
Курган 2003
Кафедра автоматизации производственных процессов
Дисциплины: “Теория автоматического управления”
(направление 657900, специальность 210200),
“Управление техническими системами ”
(направление 651400, специальность 030500),
(направление 656500, специальность 330100).
Составила: доцент, канд. техн. наук Иванова И.А.
Утверждены на заседании кафедры “ ” ___________ 2003 г.
Рекомендованы редакционно-издательским советом университета
“ ” ___________ 2003 г.
ВВЕДЕНИЕ
Для анализа САУ необходимо иметь ее математическое описание. Система разделяется на элементы и составляются уравнения, описывающие их поведение – изменение состояния во времени. Уравнения составляются на основании анализа физических, химических и иных процессов, происходящих в элементах.
Ниже рассматриваются только стационарные САУ, у которых свойства элементов не изменяются с течением времени и каждый динамический процесс (изменение состояния элемента во времени) зависит лишь от начального состояния элемента и характера внешних воздействий.
В практике широко используют представление элементов их передаточными функциями.
Контрольная работа содержит задачи по следующим темам:
- общие понятия и определения;
- логарифмические частотные характеристики и логарифмические единицы измерения;
- восстановление передаточной функции САУ по ее логарифмической характеристике (ЛАЧХ);
- определение по передаточной функции САУ типовых звеньев, входящих в ее структуру;
- определение по передаточной функции САУ значения фазовой частотной характеристики при заданном значении частоты;
- определение граничного коэффициента передачи разомкнутой цепи САУ;
- определение запасов устойчивости по амплитуде и фазе;
- передаточные функции САУ при жестких и гибких обратных связях;
- вывод передаточных функций четырехполюсников;
- расчет характеристик в статическом режиме;
- определение вида переходной характеристики по передаточной функции звена или вида ЛАЧХ.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
Передаточная функция
Передаточной функцией элемента называется отношение изображений по Лапласу выходной и входной величины при нулевых начальных условиях.
Передаточные функции элемента определяются относительно каждого из входных воздействий, при этом предполагается, что все остальные входные воздействия равны нулю.
Типовые входные воздействия и реакции на них.
На практике часто имеется резкое изменение внешнего воздействия на САУ, например, включение или выключение потребителей электрической энергии, увеличение или уменьшение момента сопротивления на валу регулируемого двигателя и т.п. Типовым изменением воздействия считают мгновенное его изменение от нуля до значения, равного единице. Для математической записи используют единичную ступенчатую функцию:
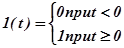
Реакция элемента или системы при нулевых начальных условиях на входную величину, являющуюся единичной ступенчатой функцией времени, называют переходной характеристикой (переходной функцией)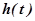 
элемента или системы.
,
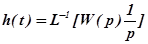где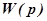 
– передаточная функция элемента или системы,
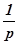- изображение единичной ступенчатой функции.
Другим часто встречающимся изменением внешних воздействий являются их кратковременные, но существенные по значению всплески, импульсы.
Нормированным импульсным воздействием считается единичный импульс, у которого произведение длительности на величину равно единице. Пределом, к которому стремится единичный импульс, когда его продолжительность стремится к нулю – единичная импульсная функция
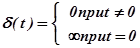
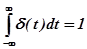- что является основным свойством 
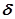- функции.
Реакцию элемента или системы на единичную импульсную функцию называют импульсной характеристикой (функцией веса)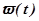 
.
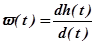
Импульсные и переходные характеристики дают информацию о поведении автоматических систем в переходных режимах. Для оценки установившихся режимов более удобно рассматривать поведение элементов и систем при воздействиях, являющихся периодическими функциями времени. В качестве таких воздействий были выбраны гармонические воздействия. Гармонические воздействия имеют следующие преимущества:
1) реально встречающиеся воздействия, как правило, могут быть представлены в виде суммы гармоник различных частот (разложение Фурье)
2) в установившихся режимах гармонические сигналы передаются линейными элементами и системами без искажений.
Если на вход стационарного линейного элемента или системы воздействует гармонический сигнал
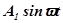
где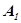 
- амплитуда
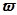- угловая частота.
Тогда на выходе с течением времени устанавливается гармонический сигнал 
той же угловой частоты, но с измененным значением амплитуды и фазы сигнала.
Отношение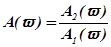 
- называется амплитудно-частотной характеристикой; 
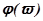- фазово-частотной характеристикой.
Эти характеристики показывают, что линейный элемент или система изменяет амплитуду и фазу гармоничного сигнала: в установившемся режиме амплитуда увеличивается или уменьшается и сдвиг фазы увеличивается или уменьшается при каждом значении угловой частоты .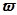
Частотные характеристики зависят от свойств элемента или системы, но не зависят от амплитуды и фазы входных гармонических сигналов.
Частотные характеристики любого объекта связаны с его передаточной функцией. Если в выражение передаточной функции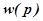 
вместо 
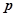подставить мнимую величину 
(подстановку Фурье), то получаем частотную передаточную функцию 
. Частотная передаточная функция является комплексной величиной,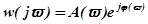 
, модуль которой равен отношению амплитуды выходного и входного сигнала, а аргумент – углу сдвига фаз между выходным и входным сигналами. Функция может быть представлена в алгебраическом виде 
, где 
- действительная часть, 
- мнимая часть частотной передаточной функции.
Амплитудно-фазовая характеристика (АФХ) представляет собой годограф (геометрическое место концов векторов) частотной передаточной функции при изменении частоты от 0 до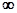 
. Характеристика строится на комплексной плоскости. Для построения АФХ выражение представляют в виде действительной и мнимой частоты путем умножения числителя и знаменателя на сопряженное знаменателю выражения. В выражениях и частоту изменяют от 0 до .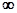
При расчетах широко используют логарифмические частотные характеристики: логарифмическую амплитудно-частотную характеристику (ЛАЧХ) и логарифмическую фазо-частотную характеристику (ЛФЧХ). При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе. Отрезок оси абсцисс, соответствующий изменению частоты в 10 раз, называется декадой. Обычно ось абсцисс начинают с частоты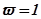 
, т.к. 
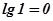. По оси ординат ЛАЧХ откладывают в равномерном масштабе логарифмическую амплитуду 
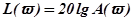в децибеллах.
ЛФЧХ имеет такую же ось абсцисс, что и ЛАЧХ, а по оси ординат откладывают в равномерном масштабе угол сдвига фаз .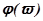
Логарифмические частотные характеристики удобны тем, что охватывают больший диапазон частот и кривые амплитудно-частотных характеристик заменяются отрезками кривых с определенными углами наклонов: 
дб/дек, 
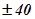дб/дек и т.д.
Физический смысл наклона – 20 дб/дек: при удесятерении частоты амплитуды выходного сигнала уменьшается в 10 раз, соответственно наклон – 40 дб/дек – означает уменьшение амплитуды в 100 раз.
Порядок построения ЛАЧХ и ЛФЧХ:
1. Определяются частоты сопряжения и расставляются по оси абсцисс.
2. Определяется первоначальный наклон характеристики, он составляет:
0 – при отсутствии интегрирующих звеньев
- 20 дб/дек – при наличии интегрирующего звена
- 40 дб/дек – при наличии двух интегрирующих звеньев
+ 20 дб/дек – при наличии дифференцирующего звена.
3. Определяется начальная точка характеристики 20 
К на частоте .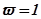
4. Первоначальный наклон характеристики продолжается до первой частоты сопряжения, после чего меняется на – 20 дб/дек, если частота сопряжения соответствует апериодическому звену I порядка, - 40 дб/дек – если колебательному звену, + 20дб/дек – если форсирующему звену.
Наклон характеристики меняется после каждой частоты сопряжения. Угол сдвига фазы определяется:
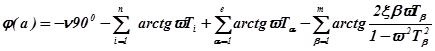
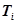- постоянная времени
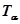- постоянная времени форсирующих звеньев
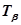- постоянная времени колебательных звеньев
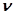- количество интегрирующих звеньев.