Построение желаемой ЛАЧХ

ЗАДАНИЕ

На курсовое проектирование по дисциплине

«Основы теории управления»

 

 

Студенту Макееву Александру Александровичу, группа 434

(фамилия, имя, отчество)

 

Направление подготовки 230100 – Информатика и вычислительная техника

Специальность 230104 – Системы автоматизированного проектирования

 

Тема Разработка программы для синтеза САУ методом ЛАЧХ

 

Исходные данные к проекту:

 

Список используемых источников:

1 Теория автоматического управления: учеб. для вузов. В 2 ч. – Ч.1: Теория линейных систем автоматического управления / Н. А. Бабаков, А. А. Воронов [ и др. ]; под ред. А. А. Воронова. – М.: Высш. шк., 1986. – 367 с.

2 Макарова, Л. Ф. Основы теории управления: конспект лекций / Л. Ф. Макарова. – СПб.: СПбГТИ(ТУ). – 2015.

3 Портал Python 2.7.4 Documentation [Электронный ресурс]: Электронные данные – Режим доступа: https://docs.python.org

4 Портал Welome to Kivy [Электронный ресурс]: Электронные данные – Режим доступа: https://kivy.org/docs

5 Портал Stack Overflow [Электронный ресурс]: Электронные данные – Режим доступа: https://stackoverflow.com

 

Требования к аппаратному программному обеспечению

Intel Core i5 3230-M 2.6 GHz, ОЗУ 6 Гб.

ОС Linux Ubuntu Mate 14.04; текстовой редактор – Sublime Text 3, средства оформления документации - Microsoft Office Word 2007.

Дата выдачи задания 17.09.2015

Дата представления курсового проекта к защите 25.12.2015

Руководитель Л.Ф. Макарова

(подпись, дата) (инициалы, фамилия)

Зав. кафедрой Т.Б. Чистякова

(подпись, дата) (инициалы, фамилия)

Задание принял(а) к выполнению студент(ка)

(подпись, дата)

Содержание

 

Цель и задачи курсового проекта 4

Введение 5

1 Аналитическая часть 6

1.1 Построение ЛАЧХ_ 6

1.2 Построение желаемой ЛАЧХ_ 7

1.3 Построение ЛФЧХ_ 8

1.4 Анализ устойчивости_ 8

2 Практическая часть 10

2.1 Анализ передаточной функции заданного соединения звеньев_ 10

2.2 Построение ЛАЧХ_ 11

2.3 Построение ЛФЧХ_ 12

2.4 Блок-схема алгоритма_ 14

2.5 Основные дисплейные фрагменты_ 15

ВЫВОДЫ_ 17

Список используемых источников 18

ПРИЛОЖЕНИЕ А_ 19

ПРИЛОЖЕНИЕ Б_ 20

ПРИЛОЖЕНИЕ В_ 25

 

 

 

Цель и задачи курсового проекта

Цель курсового проекта:

Для системы с заданной передаточной функцией разработать программу для построения асимптотической логарифмической амплитудно-частотной характеристики (ЛАЧХ) и логарифмической фазо-частотной характеристики (ЛФЧХ).

В процессе проектирования необходимо решить следующие задачи:

- провести анализ передаточных функций и логарифмических частотных характеристик типовых динамических звеньев;

- разработать алгоритм и программу построения ЛАЧХ и ЛФЧХ соединения типовых звеньев;

- разработать подпрограмму графического определения запасов устойчивости по модулю и фазе с помощью ЛАЧХ и ЛФЧХ;

- провести тестирование разработанной программы, состоящее в изменении параметров заданной передаточной функции с целью увеличения запасов устойчивости или улучшения качества функционирования системы в смысле повышения ее быстродействия.

 

Введение

В практической автоматике при расчетах АСР удобно использовать частотные характеристики, построенные в логарифмической системе координат (ЛЧХ). Применение логарифмического масштаба позволяет наглядно отображать частотные характеристики в большом диапазоне частот, представлять ЧХ отрезками ломаных линий и определять характеристики сложных систем простым суммированием или вычитанием ЛЧХ, входящих в эти системы элементов.

ЛЧХ являются исчерпывающими характеристиками системы, по которым можно восстановить ее ПФ и определить параметры.

Главное достоинство ЛАЧХ – возможность построения их во многих случаях практически без вычислений. Это проявляется в тех случаях, когда представляется в виде произведения сомножителей. Тогда результирующая ЛАЧХ находится суммированием ординат ЛАЧХ, соответствующих отдельным сомножителям.

 

 

Аналитическая часть

В теории автоматического управления широко используются логарифмические амплитудно-частотные и фазо-частотные характеристики (ЛАЧХ и ЛФЧХ). Они получаются путем логарифмирования коэффициента передаточной функции (КПФ):

ЛАЧХ получают из первого слагаемого, которое умножается на 20:

Величина откладывается по оси ординат в децибелах или белах (1 Б = 10 дБ).

Бел – единица измерения отношения мощности двух сигналов. Если мощности двух сигналов отличаются в 10 раз, то это отличие соответствует 1 Б (). Два сигнала отличаются на 1 дБ, если , что соответствует .

По оси абсцисс откладывается частота в логарифмическом масштабе, которая измеряется в декадах.

Декада – интервал частот, заключенный между произвольным значением и его десятикратным значением. Отрезок, соответствующий одной декаде равен 1. Логарифмическая шкала не имеет нуля и не может пересекаться вертикальной осью в любом месте.

ЛФЧХ, получаемая из второго слагаемого, отличается от ЛАЧХ только масштабом по оси абсцисс. Величина откладывается по оси ординат в градусах или радианах (для элементарных звеньев она не выходит за пределы ). Таким образом, при построении ЛФЧХ логарифмический масштаб применяется только для оси абсцисс.

 

Построение ЛАЧХ

При построении ЛАЧХ по оси ординат наносится равномерный масштаб, желательно кратный 20 дБ. Начало координат помещают в точке = 1. Ось абсцисс должна проходить через точку 0 дБ, что соответствует значению модуля . Точка лежит на оси частот слева в бесконечности, т.к. . В зависимости от интересующего диапазона частот ось ординат можно проводить и через другую точку так, чтобы можно было показать весь ход ЛАЧХ.

Для каждой из сопрягающих частот определяется наклон характеристики по сравнению с тем наклоном, который эта характеристика имела до сопрягающей частоты в соответствии с видом звена, представленных в таблице 1.

 

 

Таблица 1 – Наклоны ЛАЧХ типовых динамических звеньев

Вид звена	Передаточная функция	Наклон (дБ/дек)
Усилительное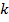
Апериодическое		-20
Колебательное		-40
Инерционное II-го порядка		-40
Дифференцирующее		+20
Форсирующее I-го порядка		+20
Форсирующее II-го порядка		+40

 

 

Построение желаемой ЛАЧХ

Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, имеющей желаемые или требуемые статические и динамические свойства. Желаемая ЛАЧХ состоит из 3-х основных асимптот:

-низкочастотной ()

-среднечастотной ()

-высокочастотной ()

Низкочастотная асимптота ЛАЧХ разомкнутой системы определяет статические свойства САУ (точность) и ее наклон зависит от порядка астатизма системы : при наклон ЛАХ равен -20 дБ/дек, при наклон ЛАХ равен -40 дБ/дек. Если передаточная функция имеет передаточный коэффициента 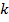и порядок астатизма , удовлетворяющие требованиям, то низкочастотной асимптотой желаемой ЛАЧХ является низкочастотная асимптота ЛАЧХ неизменяемой части системы. Если наклон низкочастотной асимптоты равен 0 или -20 дБ/дек, то наклон сопрягающей асимптоты выбирается равным -40 или -60 дБ/дек.

Среднечастотная асимптота ЛАЧХ разомкнутой системы и ее сопряжение с низкочастотной определяет динамические свойства системы (устойчивость и показатели переходной характеристики). Построение начинают с выбора частоты среза , которая определяет зависимость перерегулирования 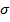и времени регулирования от максимума ВЧХ замкнутой системы, причем дано в виде функции . Среднечастотная асимптота проводится через точку с наклоном -20 дБ/дек влево и вправо от до получения определенных запасов устойчивости и допустимое перерегулирование. Протяженность устанавливается исходя из необходимого запаса устойчивости. Из этих соображений выбирают ее сопряжение с низкочастотной асимптотой. Кроме того, сопрягающую асимптоту следует выбрать так, чтобы характеристика возможно меньше отличалась от ) для того, чтобы при вычитании получалось в реализации наиболее простое КУ.

Высокочастотная асимптота мало влияет на свойства системы, поэтому ее следует выбирать так, чтобы корректирующее устройство (КУ) было возможно более простым. Это достигается при совмещении высокочастотных асимптота характеристик и . Если совмещение не удается, то высокочастотная асимптота должна иметь тот же наклон, что и высокочастотная асимптота .

Построение ЛФЧХ

Довольно часто ЛАЧХ и ЛФЧХ строятся на одном графике, чтобы давать полное представление о свойствах системы.

Для построения ЛФЧХ используется также ось частот (ось абсцисс). По оси ординат откладывается фаза в градусах (или радианах) в линейном масштабе. Положительный сдвиг по фазе откладывается по оси ординат вверх, а отрицательный – вниз.

Анализ устойчивости

Оценку устойчивости по критерию Найквиста удобнее производить по ЛЧХ разомкнутой системы. Применение метода ЛЧХ дает возможность увидеть влияние того или иного параметра системы на ее устойчивость и переходный процесс, а также позволяет сравнительно определить характеристику КУ, обеспечивающего требуемые показатели качества системы.

САУ, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если ордината ЛФЧХ на частоте среза системы по абсолютной величине меньше, чем , т.е. если .

Для того чтобы замкнутая система была устойчива необходимо и достаточно, чтобы на всех частотах, где ЛАЧХ разомкнутой системы положительная (), фазовый сдвиг не достигал или достигал его четное число раз.

Замкнутая система будет находиться на границе устойчивости, если на той же частоте среза , где ЛАЧХ разомкнутой системы обращается в 0 (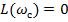), значение ФЧХ равно . Это соответствует состоянию разомкнутой системы, когда ее АФЧХ проходит через точку , т.е. когда модуль . Так как , то система будет находиться на граице устойчивости, если на частоте .

Запас устойчивости по модулю показывает, во сколько раз можно увеличить коэффициента усиления системы без потери устойчивости. Определяется на частоте, где ФЧХ дотигает значения .

Запас устойчивости по фазе определяется на частоте , где 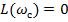и характеризует отклонение от , т.е. .

Эмпирическим путем установлено, что для нормальной работы многих систем управления необходимо обеспечивать следующие запасы устойчивости: , .

Для того, чтобы замкнутая система была устойчива необходимо и достаточно, чтобы частота, при которой ЛФЧХ пересекает линию , была больше частоты среза.

Практическая часть

Рассмотрим пример системы с передаточной функцией (ПФ):