Термины
· Единство измерений — состояние измерений, характеризующееся тем, что их результаты выражаются в узаконенных единицах, размеры которых в установленных пределах равны размерам единиц, воспроизводимым первичными эталонами, а погрешности результатов измерений известны и с заданной вероятностью не выходят за установленные пределы.
· Физическая величина — одно из свойств физического объекта, общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого из них.
· Измерение — совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения измеряемой величины с её единицей и получения значения этой величины.
· Средство измерений — техническое средство, предназначенное для измерений и имеющее нормированные метрологические характеристики воспроизводящие и (или) хранящие единицу величины, размер которой принимается неизменным в пределах установленной погрешности в течение известного интервала времени.
· Поверка — совокупность операций, выполняемых в целях подтверждения соответствия средств измерений метрологическим требованиям.
· Погрешность измерения — отклонение результата измерения от истинного значения измеряемой величины.
· Погрешность средства измерения — разность между показанием средства измерений и действительным значением измеряемой физической величины.
· Точность средства измерений — характеристика качества средства измерений, отражающая близость его погрешности к нулю.
· Лицензия — это разрешение, выдаваемое органам государственной метрологической службы на закрепленной за ним территории физическому или юридическому лицу на осуществление ему деятельности по производству и ремонту средств измерения.
· Эталон единицы величины — техническое средство, предназначенное для передачи, хранения и воспроизведения единицы величины.
3.Основное уравнение измерений
Для установления различия в количественном содержании отображаемого данной физической величиной свойства изучаемых объектов (явлений, процессов) введено понятие размера физической величины. Так, говоря о массе какого-либо тела, не следует указывать, что «величина массы тела составляет 50 кг», поскольку сама масса является физической величиной. При этом говорят о размере величины. В приведенном примере можно сказать, что «размер массы тела равен 50 кг» или проще «масса тела равна 50 кг». Итак, размер физической величины — количественная определенность физической величины, присущая конкретному материальному объекту (явлению, процессу). Истинный размер физической величины является объективной реальностью, не зависящей от того, измеряют соответствующую характеристику свойства объекта или нет. Размер величины зависит от того, какая единица принята при измерениях величины. Размер может выражаться в виде отвлеченного числа, без указания единицы измерения, что соответствует числовому значению физической величины. Количественная оценка физической величины, представленная числом с указанием единицы этой величины, называется значением физической величины. Можно говорить о размерах разных единиц данной физической величины. В этом случае размер, например, килограмма отличается от размера фунта, пуда и т. д.
Итак, если имеется некоторая величина X, принятая для нее единица измерения равна [X], то значение физической величины
X=q[X], (1)
где q — числовое значение величины X.
Например, за единицу измерения напряжения электрического тока принят 1 В. Тогда значение напряжения электрической сети
U= q [U] = 220 [1 В] = 220 В.
Здесь числовое значение q = 220. Но если за единицу напряжения принять [1 кВ], то U = q [U] = 0,22 [1 кВ] = 0,22 кВ, т. е. числовое значение q = 0,22.
Уравнение (1) называется основным уравнением измерений, показывающим, что числовое значение величины зависит от размера принятой единицы измерения.
4.Виды физических величин и единиц. Международная система единиц физических величин. Кратные и дольные единицы. Производные единицы.
Единицы физических величин и системы единиц
Единица физической величины это физическая величина такого размера, которой по определению присвоено числовое значение, равное 1. В природе физические величины связаны между собой зависимостями, которые выражают одни величины через другие. Совокупность связанных такими зависимостями величин, среди которых одни условно приняты в качестве независимых, а другие выражаются через них, называют системой величин. При этом независимые величины системы называют основными, а все другие - производными величинами. Точно также единица основной величины называется основной, а единица производной величины - производной единицей. Совокупность основных и производных единиц определенной системы величин образует систему единиц.
При построении системы единиц выбор основных величин и размера их единиц, вообще говоря, произволен. Однако, он диктуется определенными требованиями практики, основными из которых являются: число основных величин должно быть небольшим; в качестве основных должны быть выбраны величины, единицы которых легко воспроизвести с высокой точностью; размеры основных единиц должны быть такие, чтобы на практике значения всех величин выражались не слишком малыми и не слишком большими числами.
Руководствуясь этими правилами, в 1960 г. XI Генеральная конференция по мерам и весам приняла Международную систему единиц (Систему интернациональную - СИ) с основными единицами метр (m), килограмм (kg), секунда (s), ампер (A), кельвин (K), кандела (cd), моль (mol). Кроме того в качестве стандартных в системе СИ были признаны единицы, не относящиеся ни к основным ни к производным и названные дополнительными, такие как радиан (rad) и стерадиан (sr). Кроме системы СИ, используется система единиц СГС (сантиметр, грамм, секунда).
Единицы, не входящие ни в одну из известных систем, называются внесистемными, например, литр, градус, процент, децибел и т.п. Единица, которая в целое число раз больше системной или внесистемной, называется кратной единицей. Например, километр, тонна, минута, декалитр и т.п. Единица, которая в целое число раз меньше системной или внесистемной, называется дольной. Например, миллиметр, микросекунда, миллилитр и т.п. Обозначения кратных и дольных величин приводятся в справочниках.
), а остальные - со строчных (m, kg, s). Допускается использование русских обозначений (Вт, Вб, Ом, м, кг, с).Обозначения единиц, наименование которых происходит от фамилий, например Ампер, Ватт, Вебер, Ом и т.п., пишутся с прописных букв (A, W, Wb,
Кратные единицы — единицы, которые в целое число раз превышают основную единицу измерения некоторой физической величины. Международная система единиц (СИ) рекомендует следующие приставки для обозначений кратных единиц:
Дольные единицы, составляют опредёленную долю (часть) от установленной единицы измерения некоторой величины. Международная система единиц (СИ) рекомендует следующие приставки для обозначений дольных единиц:
Приставки СИ (десятичные приставки) — приставки перед названиями или обозначениями единиц измерения физических величин, применяемые для формирования кратных и дольных единиц, отличающихся от базовой в определённое целое, являющееся степенью числа 10, число раз. Десятичные приставки служат для сокращения количества нулей в численных значениях физических величин. Рекомендуемые для использования приставки и их обозначения установлены Международной системой единиц (СИ). ГОСТ 8.417-2002, регламентирующий применение СИ в России
Правила использования приставок
· Приставки следует писать слитно с наименованием единицы или, соответственно, с её обозначением.
· Использование двух или более приставок подряд (напр., микромиллифарад) не разрешается.
· Обозначения кратных и дольных единиц исходной единицы, возведенной в степень, образуют добавлением соответствующего показателя степени к обозначению кратной или дольной единицы исходной единицы, причём показатель означает возведение в степень кратной или дольной единицы (вместе с приставкой). Пример: 1 км² = (10³ м)² =106 м² (а не 10³ м²). Наименования таких единиц образуют, присоединяя приставку к наименованию исходной единицы: квадратный километр (а не кило-квадратный метр).
· Если единица представляет собой произведение или отношение единиц, приставку, или её обозначение, присоединяют, как правило, к наименованию или обозначению первой единицы: кПа·с/м (килопаскаль-секунда на метр). Присоединять приставку ко второму множителю произведения или к знаменателю допускается лишь в обоснованных случаях.
Применимость приставок
В связи с тем, что наименование единицы массы в СИ — килограмм — содержит приставку «кило», для образования кратных и дольных единиц массы используют дольную единицу массы — грамм (0,001 кг).
Приставки ограниченно используются с единицами времени: кратные приставки вообще не сочетаются с ними — никто не использует «килосекунду», хотя это формально и не запрещено, правда, из этого правила есть исключение: в космологии используется единица «гигагод» (миллиард лет); дольные приставки присоединяются только к секунде (миллисекунда, микросекунда и т. д.). В соответствии с ГОСТ 8.417-2002, наименование и обозначения следующих единиц СИ не допускается применять с приставками: минута, час, сутки (единицы времени), градус, минута, секунда (единицы плоского угла), астрономическая единица, диоптрия и атомная единица массы.
С метрами из кратных приставок на практике употребляют только кило-: вместо мегаметров (Мм), гигаметров (Гм) и т. д. пишут «тысячи километров», «миллионы километров» и т. д.; вместо квадратных мегаметров (Мм²) пишут «миллионы квадратных километров».
Приставки, соответствующие показателям степени, не делящимся на 3 (гекто-, дека-, деци-, санти-), использовать не рекомендуется. Широко используются только сантиметр (являющийся основной единицей в системе СГС) и децибел, в меньшей степени — дециметр и гектопаскаль (в метеорологических сводках), а также гектар. В некоторых странах объём вина измеряют декалитрами.
Производные единицы могут быть выражены через основные с помощью математических операций: умножения и деления. Некоторым из производных единиц, для удобства, присвоены собственные названия, такие единицы тоже можно использовать в математических выражениях для образования других производных единиц.
Математическое выражение для производной единицы измерения вытекает из физического закона, с помощью которого эта единица измерения определяется или определения физической величины, для которой она вводится. Например, скорость — это расстояние, которое тело проходит в единицу времени; соответственно, единица измерения скорости — м/с (метр в секунду).
Часто одна и та же единица может быть записана по-разному, с помощью разного набора основных и производных единиц (см., например, последнюю колонку в таблице Производные единицы с собственными названиями). Однако на практике используются установленные (или просто общепринятые) выражения, которые наилучшим образом отражают физический смысл величины. Например, для записи значения момента силы следует использовать Н·м, и не следует использовать м·Н или Дж.
5.Классификация измерений.6.Основные характеристики измерений (понятие о принципах, методах и точности измерений).
Измерение является важнейшим понятием в метрологии. Это организованное действие человека, выполняемое для количествен-ного познания свойств физического объекта с помощью определения опытным путем значения какой-либо физической величины [20].
Существует несколько видов измерений. При их классификации обычно исходят из характера зависимости измеряемой величины от времени, вида уравнения измерений, условий, определяющих точность результата измерений и способов выражения этих результатов.
По характеру зависимости измеряемой величины от времени измерения разделяются на
· статические, при которых измеряемая величина остается постоянной во времени;
· динамические, в процессе которых измеряемая величина изменяется и является непостоянной во времени.
Статическими измерениями являются, например, измерения размеров тела, постоянного давления, динамическими - измерения пульсирующих давлений, вибраций.
По способу получения результатов измерений их разделяют на
· прямые;
· косвенные;
· совокупные;
· совместные.
Прямые - это измерения, при которых искомое значение физической величины находят непосредственно из опытных данных. Прямые измерения можно выразить формулой 
, где 
- искомое значение измеряемой величины, а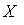 
- значение, непосредственно получаемое из опытных данных.
При прямых измерениях экспериментальным операциям подвергают измеряемую величину, которую сравнивают с мерой непосредственно или же с помощью измерительных приборов, градуированных в требуемых единицах. Примерами прямых служат измерения длины тела линейкой, массы при помощи весов и др. Прямые измерения широко применяются в машиностроении, а также при контроле технологических процессов (измерение давления, температуры и др.).
Косвенные - это измерения, при которых искомую величину определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, т.е. измеряют не собственно определяемую величину, а другие, функционально с ней связанные. Значение измеряемой величины находят путем вычисления по формуле 
, где - искомое значение косвенно измеряемой величины; 
- функциональная зависимость, которая заранее известна, 
- значения величин, измеренных прямым способом.
Примеры косвенных измерений: определение объема тела по прямым измерениям его геометрических размеров, нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения.
Косвенные измерения широко распространены в тех случаях, когда искомую величину невозможно или слишком сложно измерить непосредственно или когда прямое измерение дает менее точный результат. Роль их особенно велика при измерении величин, недоступных непосредственному экспериментальному сравнению, например размеров астрономического или внутриатомного порядка.
Совокупные - это производимые одновременно измерения нескольких одноименных величин, при которых искомую определяют решением системы уравнений, получаемых при пря-мых измерениях различных сочетаний этих величин.
Примером совокупных измерений является определение массы отдельных гирь набора (калибровка по известной массе одной из них и по результатам прямых сравнений масс различных сочетаний гирь).
Пример. Необходимо произвести калибровку разновеса, состоящего из гирь массой 1, 2, 2*, 5, 10 и 20 кг (звездочкой отмечена гиря, имеющая то же самое номинальное значение, но другое истинное). Калибровка состоит в определении массы каждой гири по одной образцовой гире, например по гире массой 1 кг. Для этого про-ведем измерения, меняя каждый раз комбинацию гирь (цифры показывают массу отдельных гирь, 
- обозначает массу образцовой гири в 1 кг):
и т.д.
Буквы 
означают грузики, которые приходится прибавлять или отнимать от массы гири, указанной в правой части уравнения, для уравновешивания весов. Решив эту систему уравнений, можно определить значение массы каждой гири.
Совместные - это производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимостей между ними.
В качестве примера можно назвать измерение электрического сопротивления при 200С и температурных коэффициентов измерительного резистора по данным прямых из-мерений его сопротивления при различных температурах.
По условиям, определяющим точность результата, измерения делятся на три класса:
1. Измерения максимально возможной точности, достижимой при существующем уровне техники.
К ним относятся в первую очередь эталонные измерения, связанные с максимально возможной точностью воспроизведения установленных единиц физических величин, и, кроме того, измерения физических констант, прежде всего универсальных (например абсолютного значения ускорения свободного падения, гиромагнит-ного отношения протона и др.).
К этому же классу относятся и некоторые специальные изме-рения, требующие высокой точности.
2. Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторого за-данного значения.
К ним относятся измерения, выполняемые лабораториями государственного надзора за внедрением и соблюдением стандартов и состоянием измерительной техники и заводскими измерительными лабораториями, которые гарантируют погрешность результата с определенной вероятностью, не превышающей некоторого, заранее заданного значения.
3. Технические измерения, в которых погрешность результата определяется характеристиками средств измерений.
Примерами технических измерений являются измерения, выполняемые в процессе производства на машиностроительных предприятиях, на щитах распределительных устройств электрических станций и др.
По способу выражения результатов измерений различают абсолютные и относительные измерения.
Абсолютными называются измерения, которые основаны на прямых измерениях одной или нескольких основных величин или на использовании значений физических констант.
Примером абсолютных измерений может служить определение длины в метрах, силы электрического тока в амперах, ускорения свободного падения в метрах на секунду в квадрате.
Относительными называются измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную.
В качестве примера относительных измерений можно привести измерение относительной влажности воздуха, определяемой как отношение количества водяных паров в 1 м3 воздуха к количеству водяных паров, которое насыщает 1 м3 воздуха при данной температуре.
Основными характеристиками измерений являются: принцип измерений, метод измерений, погрешность, точность, правильность и достоверность.
Принцип измерений - физическое явление или совокупность физических явлений, положенных в основу измерений. Например, измерение массы тела при помощи взвешивания с использованием силы тяжести, пропорциональной массе, измерение температуры с использованием термоэлектрического эффекта.
Метод измерений - совокупность приемов использования принципов и средств измерений. Средствами измерений являются используемые технические средства, имеющие нормированные метрологические свойства.
Погрешность измерений - разность между полученным при измерении X' и истинным Q значениями измеряемой величины:
Погрешность вызывается несовершенством методов и средств измерений, непостоянством условий наблюдения, а так-же недостаточным опытом наблюдателя или особенностями его органов чувств.
Точность измерений - это характеристика измерений, отражающая близость их результатов к истинно-му значению измеряемой величины.
Количественно точность можно выразить величиной, обратной модулю относительной погрешности:
Например, если погрешность измерений равна 
, то точность равна 
.
Правильность измерения определяется как качество измерения, отражающее близость к нулю систематических погрешностей результатов (т.е. таких погрешностей, которые остаются постоян-ными или закономерно изменяются при повторных измерениях одной и той же величины). Правильность измерений зависит, в част-ности, от того, насколько действительный размер единицы, в ко-торой выполнено измерение, отличается от ее истинного размера (по определению), т.е. от того, в какой степени были правильны (верны) средства измерений, использованные для данного вида измерений.
Важнейшей характеристикой качества измерений является их достоверность; она характеризует доверие к результатам измерений и делит их на две категории: достоверные и недостоверные, в зависимости от того, известны или неизвестны вероятностные характеристики их отклонений от истинных значений соответствующих величин. Результаты измерений, достоверность которых неизвестна, не представляют ценности и в ряде случаев могут служить источником дезинформации.
Наличие погрешности ограничивает достоверность измерений, т.е. вносит ограничение в число достоверных значащих цифр числового значения измеряемой величины и определяет точность измерений
7. Классификация средств измерений. Меры, измерительные преобразователи.
Средство измерений (СИ ) – техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее или хранящее единицу физической величины, размер которой принимают неизменной в течение известного интервала времени.
Приведенное определение выражает суть средства измерений, которое, во-первых, хранит или воспроизводит единицу, во-вторых, эта единица неизменна. Эти важнейшие факторы и обуславливают возможность проведения измерений, т.е. делают техническое средство именно средством измерений. Этим средства измерений отличаются от других технических устройств.
К средствам измерений относятся меры, измерительные: преобразователи, приборы, установки и системы
Меры физических величин (или просто меры) – средства измерений, воспроизводящие и хранящие физические величины одного или нескольких заданных размеров.
В свою очередь меры делятся на:
1) однозначные (например, плоско—параллельная концевая мера длины);
2) многозначные (штриховая мера длины, конденсатор переменной емкости);
3) наборы мер (набор гирь, калибров);
4) магазины мер (например, магазин электрических резисторов).
Измерительный преобразователь (англ. measuring transducer) – техническое средство с нормированными метрологическими характеристиками, служащее для преобразования измеряемой величины в другую величину или измерительный сигнал, удобный для обработки, хранения, дальнейших преобразований, индикации или передачи. (в ред. Изменения N 2, введенного Приказом Росстандарта от 04.08.2010 N 203-ст)
Примечания:
· ИП или входит в состав какого-либо измерительного прибора (измерительной установки, измерительной системы и др.), или применяется вместе с каким-либо средством измерений.
· По характеру преобразования различают аналоговые, цифро-аналоговые, аналого-цифровые преобразователи. По месту в измерительной цепи различают первичные и промежуточные преобразователи. Выделяют также масштабные и передающие преобразователи.
Примеры:
· Термопара в термоэлектрическом термометре.
· Измерительный трансформатор тока.
· Электропневматический преобразователь.
8. Классификация средств измерений. Измерительные приборы, измерительные установки и системы, измерительные принадлежности.
Измерительный прибор – средство измерений, предназна-ченное для получения значений измеряемой физической величины в установленном диапазоне. Измерительный прибор представляет измерительную информацию в форме, доступной для непосредственного восприятия наблюдателем.
По способу индикации различают показывающие и регистрирующие приборы. Регистрация может осуществляться в виде непрерывной записи измеряемой величины или путем печатания показаний прибора в цифровой форме.
Приборы прямого действия отображают измеряемую величину на показывающем устройстве, имеющем градуировку в единицах этой величины. Например, амперметры, термометры.
Приборы сравнения предназначены для сравнения измеряемых величин с величинами, значения которых известны. Такие приборы используются для измерений с большей точностью.
По действию измерительные приборы разделяют на интегрирующие и суммирующие, аналоговые и цифровые, самопишущие и печатающие.
Измерительная установка и система – совокупность функционально объединенных мер, измерительных приборов и других устройств, предназначенных для измерений одной или нескольких величин и расположенная в одном месте (установка) или в разных местах объекта измерений (система). Измерительные системы, как правило, являются автоматизированными и по существу они обеспечивают автоматизацию процессов измерения, обработки и представления результатов измерений. Примером измерительных систем являются автоматизированные системы радиационного контроля (АСРК) на различных ядерно-физических установках, таких, например, как ядерные реакторы или ускорители заряженных частиц.
Измерительные принадлежности – вспомогательные средства, служащие для обеспечения необходимых условий для выполнения измерений с требуемой точностью.
Примеры:
· Термостат.
· Барокамера.
· Специальные противовибрационные фундаменты.
· Устройства, экранирующие влияние электромагнитных полей.
· Тренога для установки прибора по уровню.
9.Классификация средств измерений по метрологическому назначению.
Средства измерений - технические средства, используемые при измерениях и имеющие нормированные метрологические свойства.
По метрологическому назначению средства измерений делятся на рабочие и эталоны.
Рабочее средства измерений - средство измерений, предназначенное для измерений, не связанное с передачей размера единицы другим средствам измерений. Рабочее средство измерений может использоваться и в качестве индикатора. Индикатор – техническое средство или вещество, предназначенное для установления наличия какой-либо физической величины или превышения уровня ее порогового значения. Индикатор не имеет нормированных метрологических характеристик. Примерами индикаторов являются осциллограф, лакмусовая бумага и т.д.
Эталон - средство измерений, предназначенное для воспроизведения и (или) хранения единицы и передачи ее размера другим средствам измерений. Среди них можно выделить рабочие эталоны разных разрядов, которые ранее назывались образцовыми средствами измерений.
Классификация средств измерений проводится и по другим различным признакам. Например, по видам измеряемых величин, по виду шкалы (с равномерной или неравномерной шкалой), по связи с объектом измерения (контактные или бесконтактные).
По назначению средства измерений разделяют на меры, измерительные преобразователи, измерительные приборы, измерительные установки и измерительные системы. По метрологическому назначению средства измерений делят на образцовые и рабочие.
Образцовые средства измерений предназначены для поверки по ним как рабочих, так и образцовых средств измерений менее высокой точности. Процесс передачи размера единиц от образцовых средств измерений высшей точности рабочим и образцовым средствам измерений более низкой точности представляет собой поверку средств измерений, поэтому все образцовые средства измерения являются средствами поверки.
Классификация средств измерения
Рабочие средства измерений применяются для измерений, не связанных с передачей размера единиц. Они предназначены для измерений размеров величин, необходимых в разнообразной деятельности человека.
Каждое средство измерения должно применяться только по своему прямому назначению. Не разрешается применять рабочие средства измерений для проведения поверочных работ; точно так же запрещается использование образцовых средств для измерений, не связанных с поверкой.
Запрещение применять образцовые средства измерений для практических измерений - одно из важнейших требований метрологии. Однако им нередко пренебрегают или недооценивают его значение. Каким бы точным не было бы средство измерений, применяемое для практических измерений, его нельзя использовать для поверки других средств измерений. Само оно должно поверяться по образцовому средству измерений, имеющему более высокую точность
10.Определение погрешности результата измерений
Непосредственной задачей измерения является определение значений измеряемой величины. В результате измерения физической величины с истинным значением Хи мы получаем оценку этой величины Хизм. - результат измерений. При этом следует четко различать два понятия: истинные значения физических величин и их эмпирические проявления – действительные значения, которые являются результатами измерений и в конкретной измерительной задаче могут приниматься в качестве истинных значений. Истинное значение величины неизвестно и оно применяют только в теоретических исследованиях.Результаты измерений являются продуктами нашего познания и представляют собой приближенные оценки значений величин, которые находятся в процессе измерений. Степень приближения полученных оценок к истинным (действительным) значениям измеряемых величин зависит от многих факторов: метода измерений, использованных средств измерений и их погрешностей, от свойств органов чувств операторов, проводящих измерения, от условий, в которых проводятся измерения и т.д. Поэтому между истинным значением физической величины и результатом измерений всегда имеется различие, которое выражается погрешностью измерений (то же самое, что погрешностью результата измерений).
Погрешность результата измерения — отклонение результата измерения от истинного (действительного) значения измеряемой величины:
Так как истинное значение измеряемой величины всегда неизвестно и на практике мы имеем дело с действительными значениями величин Хд, то формула для определения погрешности в связи с этим приобретает вид:
11.Основные источники погрешности результата измерений
Погрешность результата измерения имеет много составляю-щих, каждая из которых обусловлена различными факторами и источниками. Типичный подход к анализу и оцениванию погреш-ностей состоит в выделении этих составляющих, их изучении по отдельности и суммировании по принятым правилам. Определив количественные параметры всех составляющих погрешности и зная способы их суммирования, можно правильно оценить погрешность результата измерений и при возможности скорректировать его с помощью введения поправок.
Ниже приводятся некоторые источники появления погре-ностей измерений:
· неполное соответствие объекта измерений принятой его модели;
· неполное знание измеряемой величины;
· неполное знание влияния условий окружающей среды на измерение;
· несовершенное измерение параметров окружающей среды;
· конечная разрешающая способность прибора или порог его чувствительности;
· неточность передачи значения единицы величины от эталонов к рабочим средствам измерений;
· неточные знания констант и других параметров, используемых в алгоритме обработки результатов измерения;
· аппроксимации и предположения, реализуемые в методе измерений;
· субъективная погрешность оператора при проведении измерений;
· изменения в повторных наблюдениях измеряемой величины при очевидно одинаковых условиях и другие.
Группируя перечисленные выше и другие причины появления погрешностей измерений, их можно разделить на погрешности метода измерений, средств измерений (инструмен-та) и оператора, проводящего измерения. Несовершенство каждо-го этого компонента измерения вносит вклад в погрешность измерения. Поэтому в общем виде погрешность можно выразить следующей формулой:
где DМ – методическая погрешность (погрешность метода); DИ - инструментальная погрешность (погрешность средств измерений); DЛ - личная (субъективная) погрешность.
Основные причины возникновения инструментальной погрешности приведены в разделе о средствах измерений.
Методическая погрешность возникает из-за недостатков используемого метода измерений. Чаще всего это является следстви-ем различных допущений при использовании эмпирических зави-симостей между измеряемыми величинами или конструктив-ных упрощений в приборах, используемых в данном методе измерений.
Субъективная погрешность связана с такими индивидуальными особенностями операторов, как внимательность, сосредоточенность, быстрота реакции, степень профессиональной подготовленности. Такие погрешности чаще встречаются при большой доле ручного труда при проведении измерений и почти отсутствуют при использовании автоматизированных средств измерений.
12.Классификация погрешностей измерений по форме представления погрешности и по характеру изменения результатов при повторных измерениях
По форме представления
Абсолютная погрешность — 
является оценкой абсолютной ошибки измерения. Вычисляется разными способами. Способ вычисления определяется распределением случайной величины 
. Соответственно, величина абсолютной погрешности в зависимости от распределения случайной величины может быть различной. Если — измеренное значение, а 
— истинное значение, то неравенство 
должно выполняться с некоторой вероятностью, близкой к 1. Если случайная величина распределена по нормальному закону, то обычно за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.
Существует несколько способов записи величины вместе с её абсолютной погрешностью.
· Обычно используется запись со знаком ±. Например, рекорд в беге наHYPERLINK "https://ru.wikipedia.org/wiki/%D0%91%D0%B5%D0%B3_%D0%BD%D0%B0_100_%D0%BC%D0%B5%D1%82%D1%80%D0%BE%D0%B2" HYPERLINK "https://ru.wikipedia.org/wiki/%D0%91%D0%B5%D0%B3_%D0%BD%D0%B0_100_%D0%BC%D0%B5%D1%82%D1%80%D0%BE%D0%B2"100 метров, установленный в 1983 году, равен 9,930±0,005 с.
· Для записи величин, измеренных с очень высокой точностью, используется другая запись: цифры, соответствующие погрешности последних цифр мантиссы, дописываются в скобках. Например, измеренное значение постоянной Больцмана равно 1,3806488(13)×10−23 Дж<