Всероссийская олимпиада школьников по физике, 2014-15 учебный год
Г. Рязань
Школьный этап
Общие критерии оценок
Каждая задача оценивается целым числом баллов от 0 до 10. Если школьник довел решение задачи любым способом до полного и правильного ответа, он получает 10 баллов. Не допускается снижение оценок за плохой почерк, решение способом, отличным от авторского, и т.д. При частично правильном решении задачи применяются критерии, указанные для данной задачи. Все спорные вопросы рекомендуется решать в пользу школьника.
Возможные решения и критерии оценок по конкретным задачам
Задача 7-1, 8-1, 9-1. Петя и Вася участвуют в соревновании по бегу. Им надо пробежать три круга. Петя все время бежит со скоростью 4 м/c, а Вася первый круг пробежал со скоростью 3 м/с. С какой скоростью должен бежать Вася два оставшихся круга, чтобы догнать Петю на финише?
Возможное решение: Пусть L м - длина круга. Петя тратит на всю дистанцию 3L м при скорости 4 м/с время 3L/4 c. Вася же только на первый круг (расстояние L, скорость 3 м/с) потратил L/3 с. Следовательно, Васе надо за время 3L/4-L/3=5L/12 с пробежать расстояние 2L. Для этого Вася должен бежать со скоростью 2L:5L/12 = 4,8 м/с.
Решение можно дополнить графиком зависимости пройденного расстояния от времени.
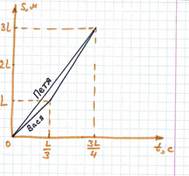
Ответ: скорость, с которой Вася должен бежать два оставшихся круга, составляет 4,8 м/с.
Критерии оценок: Если школьник довел решение задачи до правильного ответа, он получает 10 баллов. В противном случае можно поставить школьнику 2 утешительных балла, если он хотя бы раз правильно использовал формулу для скорости, времени и расстояния.
Задача 10-1, 11-1. Школьники Вася и Петя, находящиеся на расстоянии L = 20 м друг от друга, играют в мяч. Петя хочет бросить мяч так, чтобы через промежуток времени τ=2 с он попал к Васе. Под каким углом к горизонту и с какой скоростью Петя должен бросать мяч? Какой максимальной высоты (относительно точки бросания) при этом достигнет мяч? Рост школьников считайте одинаковым. Ускорение свободного падения g =10 м/с2. Сопротивлением воздуха можно пренебречь.
|
|
Возможное решение: При свободном падении мяч движется с ускорением g, направленным вниз. Поэтому движение мяча по горизонтали является равномерным со скоростью V1=L/τ. Пусть V2 - проекция начальной скорости мяча на вертикаль. Высота мяча y, отсчитываемая от точки бросания, будет зависеть от времени t как y=V2t-gt2/2. Поскольку при t=τ высота равна нулю, получим: V2=gτ/2.
Таким образом, модуль начальной скорости мяча составляет V0=(V12+V22)1/2=((L/τ)2+(gτ/2)2)1/2, а угол α, под которым надо бросать мяч, определяется из условия tg α =V2/V1=gτ2/(2L). Подстановка числовых значений дает V1=V2=10 м/с, V0=14 м/с, tg α=1 и α=45°.
Максимальная высота мяча в полете достигается, когда проекция скорости на вертикаль равна нулю, то есть в момент времени V2/g=τ/2. Эта высота равна H=gτ2/8=5 м.
Решение можно дополнить графиком зависимости вертикальной скорости мяча от времени:
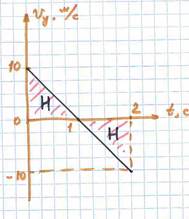
Ответ: мяч следует бросать со скоростью 14 м/с под углом 45° к горизонту; в полете он достигнет максимальной высоты 5 м.
Критерии оценок: Вопрос о модуле скорости и угле бросания оценивается из 6 баллов, вопрос о максимальной высоте подъема мяча - из 4 баллов.
|
|
Если участник довел ответ на первый вопрос до правильного ответа, он полчает за него 6 баллов (для модуля скорости допускается разброс от 13,5 м/с до 14,5 м/с). Если участник не получил правильный ответ, ему можно поставить до 4 утешительных баллов за следующие достижения (если в сумме больше 4 баллов - школьник получает по этому пункту 4 балла):
· движение по горизонтали равномерное - 1 балл;
· найдена горизонтальная скорость - 1 балл;
· записана зависимость вертикальной скорости от времени - 1 балл;
· построен график зависимости вертикальной скорости от времени - 1 балл;
· записана зависимость высоты мяча от времени - 1 балл;
· найдена начальная вертикальная скорость - 1 балл;
· модуль скорости выражен через вертикальную и горизонтальную скорости - 1 балл;
· тангенс угла, под которым брошен мяч, выражен через вертикальную и горизонтальную скорости - 1 балл;
Если участник довел ответ на второй вопрос до правильного ответа, он полчает 4 балла. Если участник не получил правильный ответ, ему можно поставить до 2 утешительных баллов за следующие достижения (если в сумме больше 2 баллов - школьник получает по этому пункту 2 балла):
· записана зависимость вертикальной скорости от времени - 1 балл;
· построен график зависимости вертикальной скорости от времени - 1 балл;
· записана зависимость высоты мяча от времени - 1 балл;
· указано, что высота подъема мяча является площадью под графиком - 1 балл;
· найдена начальная вертикальная скорость - 1 балл
Задача 7-2, 8-2. В сосуд в форме куба с длиной ребра 10 см налили воду до уровня x см. На дно сосуда ставят маленький железный кубик с длиной ребра 5 см. На какое расстояние y поднимется уровень воды в сосуде? Решите задачу в двух случаях: (а) начальный уровень воды x=1 см; (б) начальный уровень воды x=6 см. Объясните, чем отличаются эти два случая.
|
|
Возможное решение: Изначально слой воды высотой x см был распределен по площади 10∙10=100 см2. Поэтому объем воды составляет 100x см3. Исследуем, что произойдет, когда на дно поставят кубик. Пусть уровень воды поднялся на y см.
В первом случае кубик не будет покрыт водой полностью, и слой воды высотой x+y см будет распределен по площади 10∙10-5∙5=75 см2. Поэтому объем воды составит 75(x+y) см3. Учитывая, что объем жидкости не меняется, запишем уравнение: 100x=75(x+y) и y=x/3=0,33 см.
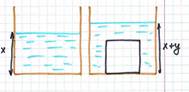Во втором случае кубик будет покрыт водой полностью. Слой воды высотой 5 см будет распределен по площади 75 см2 - объем этого слоя 75∙5=375 см3. Оставшийся слой высотой (x+y-5) см распределен по площади 100 см2. Его объем составляет 100(x+y-5) см3. Следовательно, общий объем воды (375+100(x+y-5)) см3. Поскольку объем жидкости не меняется, запишем уравнение 100x=375+100(x+y-5) - получим y=1,25 см.
Ответ: (а) уровень воды поднимется на 0,33 см; (б) уровень воды поднимется на 1,25 см; в первом случае верхняя грань кубика не покрыта водой, во втором - покрыта.
Критерии оценок: Пункт (а) оценивается в 4 балла, пункт (б) в 4 балла, объяснение отличия ситуаций пунктов (а) и (б) - в 2 балла.
Если участник довел ответ вопрос (а) до правильного ответа, он полчает за него 4 балла (допускается разброс 0,3 см - 0,4 см). Если участник не получил правильный ответ, ему можно поставить до 2 утешительных баллов за следующие достижения (если в сумме больше 2 баллов - школьник получает по этому пункту 2 балла):
· объем жидкости сохраняется - 1 балл;
· хотя бы раз правильно использована формула для объема параллелепипеда - 1 балл;
· хотя бы раз правильно использована формула для площади прямоугольника - 1 балл;
· отмечено (в тексте или на рисунке, что вода не покрывает кубик полностью) - 1 балл.
Если участник довел ответ на вопрос (б) до правильного ответа, он полчает 4 балла. Если участник не получил правильный ответ, ему можно поставить до 2 утешительных баллов за следующие достижения (если в сумме больше 2 баллов - школьник получает по этому пункту 2 балла):
· объем жидкости сохраняется - 1 балл;
· хотя бы раз правильно использована формула для объема параллелепипеда - 1 балл;
· хотя бы раз правильно использована формула для площади прямоугольника - 1 балл;
· отмечено (в тексте или на рисунке, что вода покрывает кубик полностью) - 1 балл.
Правильное объяснение отличия случаев (а) и (б) (в тексте или на рисунке) оценивается в 2 балла.
Задача 9-2, 10-2, 11-2. В сосуд в форме куба с длиной ребра 10 см налили воду до уровня x см. На дно сосуда ставят маленький железный кубик с длиной ребра 5 см. Определите, на какое расстояние y поднимется уровень воды в сосуде, в зависимости от x. Постройте график зависимости y от x.
Возможное решение: Изначально слой воды высотой x см был распределен по площади 10∙10=100 см2. Поэтому объем воды составляет 100x см3. Исследуем, что произойдет, когда на дно поставят кубик. Пусть уровень воды поднялся на y см. Следует рассмотреть следующие случаи:
(а) верхняя грань кубика находится выше уровня воды;
(б) верхняя грань кубика находится под водой.
В первом случае слой воды высотой x+y см будет распределен по площади 10∙10-5∙5=75 см2. Поэтому объем воды составит 75(x+y) см3. Учитывая, что объем жидкости не меняется, запишем уравнение: 100x=75(x+y) и y=x/3. Данный случай реализуется, если x+y<5 см, или 4x/3<5 см, или x<3,75 см.
Во втором случае кубик будет покрыт водой полностью. Слой воды высотой 5 см будет распределен по площади 75 см2 - объем этого слоя 75∙5=375 см3. Оставшийся слой высотой (x+y-5) см распределен по площади 100 см2. Его объем составляет 100(x+y-5) см3. Следовательно, общий объем воды (375+100(x+y-5)) см3. Поскольку объем жидкости не меняется, запишем уравнение 100x=375+100(x+y-5) - получим y=1,25 (см). Данный случай реализуется при x+y>5 см, или x>3,75 см.
Также следует отметить, что уровень воды не может быть больше высоты сосуда (10 см). Следовательно, при x>10-1,25 см конечный уровень воды будет не x+1,25 см, а 10 см: часть воды выльется.
Итоговый график зависимости y от x приведен на рисунке.
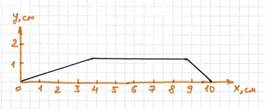
Ответ: см. график.
Критерии оценок: Оцениваются отдельные участки графика:
График проходит через точку (x=0 см;y=0 см) - 1 балл
Из точки (x=0 см;y=0 см) выходит отрезок прямой линии - 1 балл
Правильный угловой коэффициент линии, выходящей из точки (x=0 см;y=0 см) - 2 балла
На графике имеется горизонтальный участок - 1 балл
Горизонтальный участок соответствует y=1,25 см - 2 балла
График проходит через точку (x=10 см; y=0 см) - 1 балл
В точку (x=10 см; y=0 см) приходит отрезок прямой линии - 1 балл
Правильный угловой коэффициент линии, которая приходит в точку (x=10 см;y=0 см) - 1 балл
Задача 7-3. Для награждения участников Московской олимпиады школьников по физике было решено изготовить 1000 почетных грамот. Каждый квадратный метр картона для изготовления грамоты имеет массу 200 г. Размер грамоты составляет 20 см на 30 см. Какова общая масса грамот?
Возможное решение: общая площадь грамот составляет 1000∙20∙30=600000 см2=60 м2. Следовательно, масса грамот равна 200∙60=12000 г=12 кг.
Ответ: общая масса грамот составляет 12 кг.
Критерии оценок: Если школьник довел решение задачи до правильного ответа, он получает 10 баллов. В противном случае можно поставить школьнику до 3 утешительных баллов за следующие достижения:
· правильно использована формула для площади прямоугольника - 1 балл;
· использована идея, что масса грамот пропорциональна площади - 1 балл;
· хотя бы раз правильно осуществлен перевод из одних единиц измерения в другие -1 балл.
Задача 8-3, 9-3, 10-3, 11-3. Воздух можно считать состоящим из азота и кислорода: 78 процентов молекул являются молекулами азота и 22 процента - молекулами кислорода. Плотность воздуха при этом равна 1,3 кг/м3. Представим себе, что все молекулы азота заменились на атомы гелия. Найдите плотность такой газовой смеси. Массы атома гелия, молекулы кислорода и молекулы азота относятся как mгелий: mкислород: mазот=4:32:28.
Возможное решение: Пусть ρ0=1,3 кг/м3 - плотность воздуха, ρ1 - плотность новой газовой смеси, V - объем, N - общее число молекул в этом объеме. Обозначим массы атомов и молекул как mгелий =4 m, mкислород =32m, mазот=28m.
Масса воздуха в объеме V составляет, с одной стороны, ρ0V, а с другой стороны 0,78N∙28m+0,22N∙32m=28,88mN. Следовательно, ρ0V=28,88mN.
Масса новой смеси в объеме V составляет, с одной стороны, ρ1V, а с другой стороны 0,78N∙4m+0,22N∙32m=10,16mN. Следовательно, ρ1V=10,16mN.
Из двух уравнений получим: ρ1=ρ0∙10,16/28,88=0,46 кг/м3.
Ответ: плотность новой газовой смеси составляет 0,46 кг/м3.
Критерии оценок: Если школьник довел решение задачи до правильного ответа (допускается разброс 0,45 кг/м3 - 0,47 кг/м3), он получает 10 баллов. В противном случае можно поставить школьнику 2 утешительных балла, если он хотя бы раз правильно использовал формулу, связывающую массу, объем и плотность.
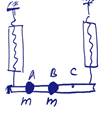
Задача 8-4, 9-4, 10-4, 11-4. Легкий горизонтальный стержень разделен точками А, В и С на четыре равные части. В точках А и В находятся грузы одинаковой массы. Концы стержня подвешены к динамометрам, как показано на рисунке. Левый динамометр показывает 1 Н. Что показывает правый динамометр?
Возможное решение: Пусть m - масса груза, F1=1 Н - показание левого динамометра, F2 - показание правого динамометра, L - длина отрезка AB. К стержню приложены две силы, направленные вниз: сила mg в точке A и такая же сила mg в точке B, а также силы, направленные вверх: сила F1 в точке D и сила F2 в точке E.
Запишем правило рычага, считая осью вращения точку D: F2∙4L=mg∙L+mg∙2L; из него получаем F2=3mg/4.
Также запишем правило рычага, считая осью вращения точку E: F1∙4L=mg∙3L+mg∙2L; из него получим F1=5mg/4.
Следовательно, F2=3F1/5=0,6 Н.
Ответ: правый динамометр покажет 0,6 Н.
Критерии оценок: Если школьник довел решение задачи до правильного ответа, он получает 10 баллов. В противном случае можно поставить школьнику до 4 утешительных баллов за следующие достижения (если в сумме больше 4 баллов - школьник получает по этому пункту 4 балла):
· высказывается идея об использовании правила рычага или правила моментов - 1 балл;
· на рисунке нарисованы все силы и их точки приложения - 1 балл;
· указано, что сила тяжести равна mg - 1 балл;
· отмечается, что равнодействующая сил должна обращаться в нуль - 1 балл;
· отмечено, что момент силы равен произведению силы на плечо - 1 балл;
· правильно подсчитано плечо хотя бы одной силы - 1 балл.
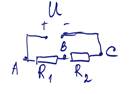Задача 9-5, 10-5. Школьник Ярослав проводит опыты с электрической цепью, схема которой изображена на рисунке, и вольтметром. При подсоединении к клеммам А и В, вольтметр показал напряжение U1 = 2 В, а при подсоединении к В и С - то же самое напряжение U1 = 2 В. Ярослав подумал, что при подсоединении к клеммам А и С вольтметр покажет 4 В, однако почему-то вольтметр показал U0=4,4 В. Объясните ход рассуждений Ярослава. Считая, что сопротивление вольтметра равно RV=100 кОм, найдите сопротивления резисторов в схеме и напряжение источника. Источник считайте идеальным.
Возможное решение: Если бы вольтметр был идеальным (имел бы бесконечное сопротивление), он показывал бы сначала напряжение между клеммами A и B, а затем - между клеммами B и C. В этом случае при подключении к клеммам A и C он показал бы сумму напряжений, то есть 2 В+2 В=4 В. Поэтому рассуждения Ярослава относятся к идеальному вольтметру.
Однако, как сказано в условии, вольтметр имеет конечное сопротивление RV. При его включении между точками A и B схема принимает вид, представленный на рисунке.
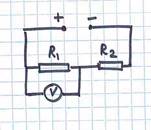
По формулам последовательного и параллельного соединения проводников, общее сопротивление цепи составляет R2+RAB, где RAB=R1RV/(R1+RV). Следовательно, сила тока в цепи равна U/(R2+RAB), а напряжение на вольтметре окажется равным U1=URAB/(R2+RAB). Данное соотношение удобно записать как U/U1-1=R2/RAB, или (U/U1-1)/R2=1/R1+1/RV.
Рассматривая подключение вольтметра к контактам B и C, по аналогии получим:
(U/U1-1)/R1=1/R2+1/RV.
При подключении вольтметра к клеммам A и C его показание равно напряжению батарейки U=U0.
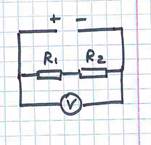
Таким образом, получена система уравнений:
(U0/U1-1)/R2=1/R1+1/RV, (U0/U1-1)/R1=1/R2+1/RV.
Подставляя числовые значения, приводим систему к виду:
1,2/R2=1/R1+1/RV, 1,2/R1=1/R2+1/RV
и
R1=R2=0,2RV=20 кОм.
Ответ: Ярослав считал, что вольтметр идеальный и должно быть U0=U1+U1; напряжение источника равно 4,4 В, сопротивления резисторов R1=R2=20 кОм.
Критерии оценок: Объяснение хода первоначальных рассуждений Ярослава оценивается из 2 баллов, пункт о напряжении источника - из 2 баллов; пункт о сопротивлении резисторов - из 6 баллов.
Если участник правильно передал ход рассуждений Ярослава, он получает за этот пункт 2 балла.
За правильный ответ на вопрос о напряжении источника участник получает 2 балла. Утешительных баллов при неправильном ответе не предусмотрено.
Если участник получил правильные значения сопротивлений, он получает за пункт 6 баллов. Если участник не получил правильный ответ, ему можно поставить до 3 утешительных баллов за следующие достижения:
· нарисованы схемы с различными подключениями вольтметра - 1 балл;
· хотя бы раз правильно использован закон Ома - 1 балл;
· получено правильное соотношение, выражающее напряжение вольтметра через напряжение источника, хотя бы для одной из схем подключения - 1 балл
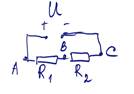Задача 11-5. Школьник Владислав проводит опыты с электрической цепью, схема которой изображена на рисунке, и вольтметром. При подсоединении к клеммам А и В, вольтметр показал напряжение U1 = 2 В, а при подсоединении к В и С - напряжение U2 = 2,5 В. Владислав подумал, что при подсоединении к клеммам А и С вольтметр покажет 4,5 В, однако почему-то вольтметр показал U0=5 В. Объясните ход рассуждений Владислава. Считая, что сопротивление вольтметра равно RV=100 кОм, найдите сопротивления резисторов в схеме и напряжение источника. Источник считайте идеальным.
Возможное решение: Если бы вольтметр был идеальным (имел бы бесконечное сопротивление), он показывал бы сначала напряжение между клеммами A и B, а затем - между клеммами B и C. В этом случае при подключении к клеммам A и C он показал бы сумму напряжений, то есть 2 В+2 В=4 В. Поэтому рассуждения Владислава относятся к идеальному вольтметру.
Однако, как сказано в условии, вольтметр имеет конечное сопротивление RV. При его включении между точками A и B схема принимает вид, представленный на рисунке. По формулам последовательного и параллельного соединения проводников, общее сопротивление цепи составляет R2+RAB, где RAB=R1RV/(R1+RV). Следовательно, сила тока в цепи равна U/(R2+RAB), а напряжение на вольтметре окажется равным U1=URAB/(R2+RAB). Данное соотношение удобно записать как U/U1-1=R2/RAB, или (U/U1-1)/R2=1/R1+1/RV.
Рассматривая подключение вольтметра к контактам B и C, по аналогии получим:
(U/U2-1)/R1=1/R2+1/RV.
При подключении вольтметра к клеммам A и C его показание равно напряжению батарейки U=U0.
Таким образом, получена система уравнений:
(U0/U1-1)/R2=1/R1+1/RV, (U0/U2-1)/R1=1/R2+1/RV.
Подставляя числовые значения, приводим систему к виду:
1,5/R2=1/R1+1/RV, 1/R1=1/R2+1/RV
и
R2=0,25RV=25 кОм, R1=0,2RV=20 кОм.
Ответ: Владислав считал, что вольтметр идеальный и должно быть U0=U1+U2; напряжение источника равно 5 В, сопротивления резисторов R1=20 кОм, R2=25 кОм.