Расчетно-графическое задание №2
по дисциплине «Физическая химия»
раздел «Химическая кинетика» и «Адсорбция»
Выполнил: Студент гр. ТСМб-15-2 (подпись) Р. А.Давлеткулова
Проверил: Доц., канд.техн.наук (подпись) С.В.Юдина
Магнитогорск
Исследование I
раздел «Химическая кинетика»
Для реакции А + В → продукты реакции начальные концентрации веществ А и В С0(А) = С0(В) = С0=1 моль/дм3. Изменение концентрации веществ А и В во времени представлено в табл. 1. Найти энергию активации и время, за которое 32% исходных веществ при температуре Т5 = 700 К превратятся в продукты реакции.
Найти энергию активации (Е), предэкспоненциальный множитель (kо) и время (τ5), за которое 32 % исходных веществ А и В при температуре Т5 = 700 К превратится в продукты реакции.
Исходные данные для исследования 1 раздел «Химическая кинетика»
| Время τi, с | Изменение концентрации Сi вовремени при температуре |
Т 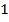
|
Т 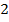
|
Т 
|
Т 
|
Т 
| % прореагировавшего вещества | ||||||
Т 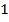
| Т 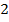
| Т 
| Т 
| ||||||||||
| С | С | С | С | С | С | С | С | С | С | ||||
| 1,0 | 0,85 | 0,5 | 0,3 | 1,0 | 0,87 | 1,0 | 0,89 | 1,0 | 0,91 |
1.1. Определение порядка реакции методом Вант – Гоффа
Логарифмируем уравнение закона действия масс V = k  (3) получим выражение: lgV = lgk + n lgC, (4), которое в координатах lgС –lgV имеет вид прямой. Для построения такой зависимости необходимо иметь несколько значений скорости химической реакции Vi при нескольких концентрациях Сi. Определим эти скорости графически из кинетической кривой (рисунок 1), построенной по данным табл. 1 для
(3) получим выражение: lgV = lgk + n lgC, (4), которое в координатах lgС –lgV имеет вид прямой. Для построения такой зависимости необходимо иметь несколько значений скорости химической реакции Vi при нескольких концентрациях Сi. Определим эти скорости графически из кинетической кривой (рисунок 1), построенной по данным табл. 1 для 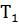 = 1000 К.
= 1000 К.
Скорость реакции V определяем для пяти произвольно выбранных концентраций  = 0,8 моль/
= 0,8 моль/  ;
; 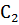 = 0,7 моль/
= 0,7 моль/  ;
;  = 0,6 моль/
= 0,6 моль/  ;
;
 = 0,5 моль/
= 0,5 моль/  ;
;  = 0,4 моль/
= 0,4 моль/  как тангенс угла наклона касательной и кинетической кривой в точке пересечения значения концентрации с кривой:
как тангенс угла наклона касательной и кинетической кривой в точке пересечения значения концентрации с кривой:
V  =
= 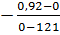 =7,603*
=7,603*  моль/
моль/  *с
*с
V  =
=  =8,750*
=8,750*  моль/
моль/  *с
*с
V  =
=  =7,652*
=7,652*  моль/
моль/  *с
*с
V  =
=  =6,666*
=6,666*  моль/
моль/  *с
*с
V  =
=  =5,175*
=5,175*  моль/
моль/  *с
*с
Аналогично определяю скорости при других концентрациях и результаты расчета свожу в таблицу 4.
Таблица 4
Скорость реакции Vi при различных концентрациях Сi.
Сi, моль/ 
| 0,8 | 0,7 | 0,6 | 0,5 | 0,4 |
Vi*  , моль/дм3∙с , моль/дм3∙с
| 7,603 | 8,75 | 7,652 | 6,666 | 5,175 |
| -lgC | 0,097 | 0,155 | 0,222 | 0,301 | 0,398 |
| -lgV | 2,119 | 2,058 | 2,116 | 2,176 | 2,286 |
По данным таблицы 4 строю график в координатах lgC - lgV для определения порядка реакции (см. уравнение 4), тангенс угла которого равен  .
.
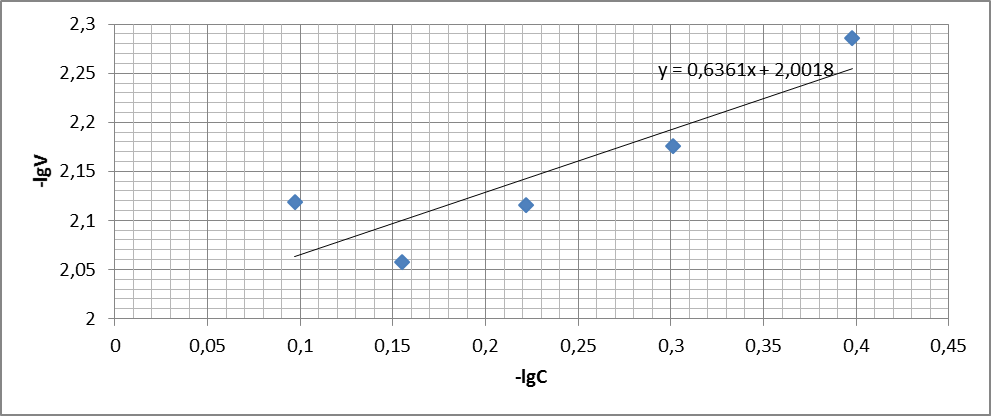
Рисунок 2 - Зависимость десятичного логарифма скорости реакции V от десятичного логарифма концентрации С.
 =tgα=
=tgα=  =1,123.
=1,123.
1.2. Определение порядка реакции по периоду полупревращения
Для определения порядка реакции вторым способом необходимо из графика (см. рисунок 1) определить несколько периодов полупревращения, например, для  = 1,0 моль/
= 1,0 моль/  ;
;  = 0,90 моль/
= 0,90 моль/  ;
; 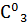 = 0,80 моль/
= 0,80 моль/  ;
;  = 0,70 моль/
= 0,70 моль/  .
.
На рисунке 1, показано как определить  для
для 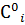 =0,90 моль/
=0,90 моль/  . Для этого из ординаты
. Для этого из ординаты 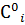 =0,90 моль/
=0,90 моль/  провожу линию, параллельную оси абсцисс до пересечения с кривой. Аналогичную линию провожу из ординаты
провожу линию, параллельную оси абсцисс до пересечения с кривой. Аналогичную линию провожу из ординаты 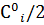 = 0,45 моль/
= 0,45 моль/  . Период полупревращения
. Период полупревращения  определяю из выражения:
определяю из выражения:
 =
=  -
-  = 60 – 6 = 54 с.
= 60 – 6 = 54 с.
Определив  для всех концентраций, свожу данные в таблицу 5.
для всех концентраций, свожу данные в таблицу 5.
 =
=  -
-  = 51 – 0 = 51 с.
= 51 – 0 = 51 с.
 =
=  -
-  = 68 - 15 = 53 с.
= 68 - 15 = 53 с.
 =
=  -
-  = 79 - 25 = 54 с.
= 79 - 25 = 54 с.
Таблица 5
Период полупревращения  при различных исходных концентрациях
при различных исходных концентрациях 
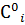 , моль/ , моль/ 
| 1,00 | 0,90 | 0,80 | 0,70 |
 , c , c
| ||||

| 0,046 | 0,097 | 0,155 | |
-lg 
| 1,71 | 1,73 | 1,72 | 1,73 |
Период полупревращения связан с порядком реакции уравнением:
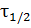 =
=  *
*  (5)
(5)
Обозначив отношение  = B и прологарифмировав (5), получу:
= B и прологарифмировав (5), получу:
lg 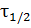 = lgB + (1 – n)*lg
= lgB + (1 – n)*lg  (6)
(6)
Выражение (6) является уравнением прямой в координатах lg 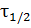 - lg
- lg  . Построю эту прямую на рисунке 3 и определю порядок из уравнения:
. Построю эту прямую на рисунке 3 и определю порядок из уравнения:
 = 1 – tg α. (7)
= 1 – tg α. (7)

Рисунок 3 - Зависимость десятичного логарифма периода полупревращения 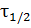 от исходной концентрации
от исходной концентрации  .
.
Определяю из рисунка 3 тангенс угла наклона прямой tgα:
tgα =  =
= 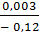 = - 0,025
= - 0,025
Из уравнения (7) определим порядок  = 1- (-0,025) =1,025
= 1- (-0,025) =1,025
Поскольку порядки, найденные разными способами различны, то истинный порядок определяю как среднее между двумя значениями:
n=  =
= 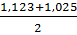 ͌ 1,074
͌ 1,074
Следует отметить, что при  < 1 характер наклона прямой на рисунке 2 будет «убывающий», а tgα > 0. При n1 = 1 на рисунке 3 будет прямая, параллельная оси абсцисс, т.к. для первого порядка полупревращения не зависит от исходной концентрации.
< 1 характер наклона прямой на рисунке 2 будет «убывающий», а tgα > 0. При n1 = 1 на рисунке 3 будет прямая, параллельная оси абсцисс, т.к. для первого порядка полупревращения не зависит от исходной концентрации.
Подставив в уравнение (1) найденный порядок реакции, определю вид кинетического уравнения:
 =
=  (
( (1)
(1)
 =
=  (
( (8)
(8)
По уравнению (8), зная исходные концентрации  и текущие -
и текущие -  в момент
в момент 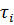 , можно рассчитать константы скорости при требуемых температурах
, можно рассчитать константы скорости при требуемых температурах 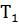 -
-  . Значения исходных и текущих концентраций через 10 с от начала реакции возьму из таблицы 3.
. Значения исходных и текущих концентраций через 10 с от начала реакции возьму из таблицы 3.
 =
=  (
( – 1) = 16,40 *
– 1) = 16,40 * 

 Т = 1000 К
Т = 1000 К
 =
=  (
( – 1) = 13,64 *
– 1) = 13,64 * 

 Т = 952 К
Т = 952 К
 =
=  (
( – 1) = 12,26 *
– 1) = 12,26 * 

 Т = 909 К
Т = 909 К
 =
=  (
( – 1) = 9,52 *
– 1) = 9,52 * 

 Т=870 К
Т=870 К
1.3. Определение энергии активации и предэкспоненциального множителя
Зависимость константы скорости k от температуры Т описывается основным уравнением химической кинетики (уравнением Аррениуса):
k = *  (9)
(9)
где  - предэкспоненциальный множитель;
- предэкспоненциальный множитель;
е - основание натурального логарифма;
Е – энергия активации;
R – универсальная газовая постоянная.
В малом интервале температур (до 200 К) величины  и Е изменяются незначительно и их можно считать постоянными. Это допущение дает возможность определить их значения графически. После логарифмирования уравнения (9):
и Е изменяются незначительно и их можно считать постоянными. Это допущение дает возможность определить их значения графически. После логарифмирования уравнения (9):
ln k = ln  -
-  *
*  (10)
(10)
Видно, что в координатах ln k -  график этой функции представляет собой
график этой функции представляет собой
прямую, тангенс угла наклона которой есть отношение Е/ R, т.е.
tgα=  (11)
(11)
Для построения графика свожу ранее определенные данные в таблицу 6.
Таблица 6
Значение константы скорости  при различных температурах
при различных температурах 
 , К , К
| ||||

| 16,40 | 13,64 | 12,26 | 9,52 |
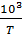 , , 
| 1,050 | 1,100 | 1,149 | |

| 4,110 | 4,293 | 4,401 | 4,654 |
По данным таблицы 6 построена зависимость, представленная на рисунке 4.

Рисунок 4 - Зависимость логарифма константы скорости от обратной температуры
Из рисунка 4 определяю тангенс наклона:
tgα = 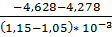 =
=  = - 3 500
= - 3 500
и затем из уравнения (11) энергию активации:
Е = 3 500 * 8,31 = 29 085 (Дж/моль)
Значение предэкспоненциального множителя найду из уравнения (10), подставив в него любую пару значений ln k и  , взятых из рисунка 4.
, взятых из рисунка 4.
Например, при  = 1,15 *
= 1,15 *  ; ln k = - 4,628.
; ln k = - 4,628.
Тогда:  = ln k +
= ln k +  *
*  = - 4,628 +
= - 4,628 +  *1,15*
*1,15*  = - 0,603
= - 0,603
Откуда  =
=  = 0,547
= 0,547
Итак, все постоянные в уравнениях (9.10) известны. Нахожу  при
при  = 700 К.
= 700 К.
 = -0,603 -
= -0,603 -  *
*  = -5,603
= -5,603
 =
=  = 3,687 *
= 3,687 * 
 *
* 
Используя выражение (8) рассчитаю время, за которое 32% исходных веществ превратятся в продукты реакции, т.е. их концентрация изменится от значения Со = 1,0 моль /  до значения С = 0,43*Со моль /
до значения С = 0,43*Со моль /  при температуре 700 К.
при температуре 700 К.
τ =  * (
* ( ) = 236,2 с
) = 236,2 с
Таким образом, при температуре 845К, при исходных концентрациях реагирующих веществ Со(А)=Со(В)=Со=1 моль/  32% исходных веществ прореагирует за 236,2 с.
32% исходных веществ прореагирует за 236,2 с.