Интегральная теорема Муавра-Лапласа.

Pn(m)=P(mn=m) → Теорема: Если m есть число наступления события (число успехов) в n НЗ испытаниях, в любом из которых успех появляется с вероятностью р (0<p<1), то равномерно относительно a,b (-∞£a£b£+∞) при n→∞ имеет место соотношение: . Доказательство: Обозначим через ;

Введем приращение: Δхm =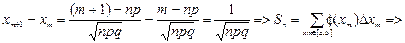

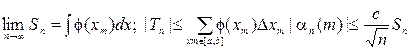Но таким образом ЧТД. То что мы доказали позволяет нам записать следующее P(a£x£b)=Ф(b)–Ф(а), где Ф(х)= - функция Лапласа. Ее значения табулированы. Свойства ф-ии Лапласа: (1) Ф(–х)= –Ф(х) (2) Ф(х)→0,5 при х³4,5

Ф(а)=Ф(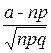); Ф(b)=Ф()

 

 

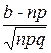10.4. Отклонение относительной частоты от постоянной вероятности в независимых испытаний.

используем интегральную теорему Муавра-Лапласа, которая позволяет оценить близость частоты и вероятности. 0<p<1 mn – общее число успехов. mn / n – частота успеха. Если n велико, то используя теорему Муавра Лапласа можно записать 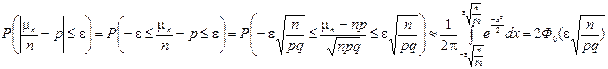Итак, мы получили . Задача. Вероятность появления события в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что относительная частота m/n появления события отклонится от его величины не более чем на 0,04. Решение n=625 p=0.8 q=0.2

10.5. Обратная задача к схеме Бернулли. Задача.

Сколько нужно провести испытаний, чтобы частота mn / n отклонилась то вероятности р не более чем на ε с вероятностью 1–2a, где a-мало . При этом решение зависит от неизвестной р, этой зависимости можно избежать, если потребовать чтобы вероятность отклонения была ³1–2a. То есть перейти к оценке

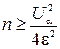=> . Задача. Найти число испытаний n при котором с вероятностью 0,7698 можно ожидать что относительная частота появления события отклонится не более чем на 0,02.

Решение:

.

 

11.1. Функция распределения. Свойства функции распределения.

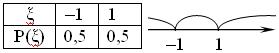Случайная величина – одно из основных понятий теории вероятности. Примеры: 1. число вызовов на АТС в течении определенного времени. 2. число космических частиц, попадающих на определенный участок земли и так далее… Все эти примеры с точки зрения математики представляют одну и туже картину, а именно, мы имели дело с величиной, так или иначе характеризующую исследуемое явление, которое под влиянием различных обстоятельств способно принимать различные значения, предсказать которые заранее нельзя. Т.о чтобы знать случайную величину необходимо знать ее значение, которое оно может принимать и вероятности с которыми она может принимать эти значения. Для этого вводится понятие функции распределения случайной величины. Определение: Пусть ξ – случайная величина, х – произвольное действительное число. Вероятность того, что ξ примет значение < х называется функцией распределения вероятностей случайной величины ξ. . Случайная величина – это величина, значение которой зависит от случая и для которой определена функция распределения вероятностей. Пример1. два игрока подбрасывают монетку, если герб – то первому рубль, если решка, первый отдает рубль. W={“Г”, “Р”} Р(“Г”)=Р(“Р”)=0,5 ξ – Случайная величина ξ= ξ(“Г”)= 1 ξ= ξ(“Р”)= –1. Строим табличку

Свойства функции распределения:

(1) Î[0, 1] так как по определению = Р(ξ<x)Î [0,1]. (2) "х1,х2 х1<x2, => £ Доказательство {ξ<x1}Ì{ ξ<x2} при х1<x2 тогда Р(ξ<x1)£ Р(ξ<x2) => £
Следствие: P(a< ξ<b)= – Следствие: вероятность того, что случайная величина принимает ровно одно значение равна 0. (3) . Доказательство: возьмем послед. событий {ξ<–n} n=1,2,…она монотонно убывает.{ξ<–n}É{ξ<–n–1} n=1,2,… =Æ => P(Æ)=0. Отсюда, с учетом монотонности . Случай x→+∞ аналогично. (4) функция распределения непрерывна слева, то есть . Док-во. Пусть числовая последовательность yn возрастает, тогда {ξ<yn}É{ξ< yn+1} учитывая монотонность получим требуемое. ОПРЕДЕЛЕНИЕ: любая ф-ия распределения является неубывающей, непрерывной слева и удовлетворяет условиям . Обратное тоже верно. Ф-ия удовл перечисленным условиям может являться функцией распределения некоторой случайной величины. Замечание: любая случайная величина однозначно определяет свою функцию распределения, но существует сколько угодно случайных величин, имеющих одну и туже ф-ию распределения.

 

 

11.2. Дискретные и абсолютно непрерывные распределения.

Иногда поведение случайной величины характеризуется вовсе не задание ее функции распределения, а каким-либо другим способом. Всякая такая характеристика носит название закона распределения случайной величины, если только по определенным правилам можно получит из нее функцию распределения. Закон распределения называется дискретным, если существует конечное или счетное множество чисел х1,х2,… без точек накопления, таких что Р(ξ=xk)=pk ³0, k=1,2,…,n и

Случайная величина имеющая дискретный закон распределения называется дискретной. Закон распределения величины ξ называется абсолютно непрерывным, если существует ф-ия Pξ(x)³0: Fξ(x)= с Случайная величина, имеющая непрерывно распределение называется абсолютно непрерывной. Функция Pξ(x) – плотность распределения вероятности случайной величины ξ. (проще – плотность вероятностей).

 

11.3. Свойства плотности распределения вероятностей. Наиболее распространенные распределения.

Функция Pξ(x) – плотность распределения вероятности случайной величины ξ. (проще – плотность вероятностей). Предполагают, что эта функция непрерывна всюду, за исключение конечного числа точек. Свойства Pξ(x): (1) Pξ(x)³0 (2) (3) Pξ(x)= (4) P(a£ ξ £b)= . Замечание: ф-ию распределения иногда называют интегральной функцией случайной величины ξ, а плотность – дифференциальной ф-ие сл. величины ξ. Наиболее часто встречающиеся распределения:

I дискретные случайные величины: 1.вырожденные случайные величины Р(ξ=а)=1 а=const 2. гипергеометрическое 2.-5. – перекатать табличку (легальную шпору 1-4)

II непрерывные случайные величины. Перекатать табличку (5-до конца)

 

 

12.1. Многомерные функции и плотности распределения вероятностей, свойства.

Определение: пусть на вероятностном пространстве (W, U, P) заданы n-случайных величин ξ1=f1(w), ξ2=f2(w),…, ξn=fn(w) wÎW fi(w) – измеримы, тогда вектор (ξ1, ξ2,…, ξn) – называется случайным вектором или n-мерной случайной величиной. ξ= (ξ1, ξ2,…, ξn). Совместные ф-ии распределения (или многомерные функции распределения если n- мерная функция распределения) n-мерной случайной величины (или случайного вектора) ξ= (ξ1, ξ2,…, ξn) называется вероятностью. Fξ(x)=Fξ1ξ2…ξn(x1,x2,…,xn) = Р{ξ1<x1, ξ2<x2,…, ξn<xn} рассмотренная как функция точки (x1,x2,…,xn)Î Rn n-мерного евклидова пространства. Свойства многомерной функции распределения. (1) Fξ(x)=Fξ1ξ2…ξn(x1,x2,…,xn) – неубывающая функция по любому аргументу. (2) Fξ(x)-непрерывна слева по любому аргументу. (3) Fξ(+∞)=Fξ1ξ2…ξn(+∞,+∞,…,+∞)=1 k=1,2,…,n при произвольных значениях остальных аргументов. (4) при любых ai,bi i=1,2,…,n выражение Р{a1£ξ1£b1, a2£ξ2£b2,…,an£ξn£bn} такая что " x1,x2,…,xn имеет место равенство Fξ(x)=Fξ1ξ2…ξn(x1,x2,…,xn) = F(b1,b2,…,bn)= = - неотрицательные pij…k – есть значение функции распределения F(c1,c2,…,cn), когда ai=ci, aj=cj, ak=ck, а остальные cs=bs. Замечание: в одномерном случае необходимо и достаточно было трех первых свойств для функции распределения.
Если существует такая Pξ(x)= Fξ(x)=Pξ1ξ2…ξn(x1,x2,…,xn), что такая что " x1,x2,…,xn имеет место равенство Fξ(x)=Fξ1ξ2…ξn(x1,x2,…,xn) = , то эта функция называется плотностью распределения вероятности случайного вектора или n-мерной плотностью (или многомерной совместной плотностью). Свойства плотности (1) Fξ(x)=Fξ1ξ2…ξn(x1,x2,…,xn)³0
(2) вероятность попадания точки в область G Р{(ξ1, ξ2,…, ξn)Î G}=
(3)

 

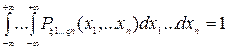
12.2. Независимость случайных величин.

Определение: случайные величины ξ1, ξ2,…, ξn называются независимыми, если для любых действительных чисел х2,…, хn n=1,…,n Fξ1ξ2…ξn(x1,x2,…,xn) = Fξ1(x1)*… *Fξn(xn). Если совместные функции распределения системы случайных величин (случайного вектора) ξ1, ξ2,…, ξn совпадает с произведением Fξ1ξ2…ξn(x1,x2,…,xn) = Fξ1(x1)*…*Fξn(xn) где Fξk(xk) k=1,2,…,n, удовлетворяет соотношениям Fξk(+∞)=1 k=1,2,…,n, то величины ξ1, ξ2,…, ξn независимы и функции Fξk(xk) являются их функциями распределения. Если независимые величины ξ1, ξ2,…, ξn - непрерывны и имеют плотность распределения Pξ1(x1)*… *Pξn(xn), то n-мерная случайная величина или n-мерный вектор имеет плотность Pξ1ξ2…ξn(x1,x2,…,xn) = Pξ1(x1)*… *Pξn(xn). Пример. Пусть компоненты случайного вектора ξ1, ξ2,…, ξn – независимы, случайно распределены по нормальному закону распределения Fξk(xk)= Совместное распределение Fξ1ξ2…ξn(x1,x2,…,xn)= = Pξ1ξ2…ξn(x1,x2,…,xn)=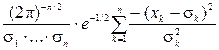

Рассмотрим дискретную двумерную случайную величину (ξ1, ξ2). Определение: законом распределения двумерной случайной величины (ξ1, ξ2) называют множество пар всевозможных пар чисел (xi, yj) и соответствующих вероятностей Р(xi, yj). Двумерную дискретную случайную величину можно трактовать как точку с координатами А(ξ1, ξ2) на координатной плоскости. Закон распределения задается в виде таблицы с двумерным кодом. Где prk = P{ξ1 = xk, ξ2 = yr} k=1,…,n r=1,…m Из это таблицы можно найти закон распределения любой из случайных компонент, то есть одномерные законы распределения. P{ξ1 = xk}=p1k+p2k+…+pmk k=1,…,n или P{ξ2 = yr}=pr1+pr2+…+pr n r=1,…,m =>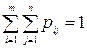

 

13. Функции от случайных величин

Постановка задачи. По функции распределения Fξ1ξ2…ξn(x1,x2,…,xn) совокупности случайных величин ξ1,ξ2,…,ξn определить функцию распределения Фη1η2…ηn(y1,y2,…,yk) в совокупности случайных функций η1=f1(ξ1,ξ2,…,ξn), η1=f1(ξ1,ξ2,…,ξn),…, ηk=fk(ξ1,ξ2,…,ξn). Искомая функция распределения Ф в случае непрерывных случайных величин ищется с помощью интеграла
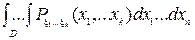= , где область интегрирования D = {(x1,…,xn): fi(x1,…,xn)<yi, i=1,2,…k} В случае дискретных случайных величин используем n-мерную сумму распределенную на области D. Теорема: если две случайные величины ξ1,ξ2 независимы => независимы и их ф-ии распределения случайных величин η1=f1(ξ1,ξ2), η2=f2(ξ1,ξ2). Теорема: Если случайная величина ξ распределена нормально ξ: (a,σ2) то линейная функция ее так же имеет нормальное распределение с параметрами А и В. η=Аξ+В, А и В-const: (Аa+В; А2σ2). Доказательство: случай 1: А>0 => Fη(x)=P{η<x}=P{Аξ+В<x} =P{ξ<(x-B)/A}= => {отсюда ввиду непрерывности случайного аргумента ξ Pξ(x) "x} => Pη=Fη'(x)=Pξ((x-B)/A)-∞ × ((x-B)/A)' = 1/A* Pξ((x-B)/A) случай 2: А<0 Fη(x)=P{Аξ+В<x} =P{ξ>(x-B)/A}= => {отсюда ввиду непрерывности случайного аргумента ξ Pξ(x) "x} => Pη(x)=
= –1/A* Pξ((x-B)/A). Обобщая два результата получаем: Pη(x)= 1/|A|* Pξ((x-B)/A)= где (a1,σ1) = (Аa+В; |А|σ)

Теорема: если ξ1 и ξ2 абсолютно непрерывны и независимы, то случайные величины ξ1+ξ2 также абсолютно непрерывная случайная величина и плотность определяется по формуле Pξ1+ξ2 (X)= 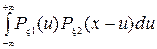Доказательство: Fξ1+ξ2 (X)=P{ξ1+ξ2 < x}=P{ ξ1+ξ2 £ Dx} Dx={(u,v): u+v<x} Из независимости ξ1,ξ2 совместная плотность Рξ1ξ2(u,v)= Рξ1(u)Рξ2(v) => Fξ1+ξ2 (X) = = = ЧТД.

 

14.1. Математическое ожидание случайной величины, свойства, примеры, мат ожидание наиболее распространенных распределений.

Математическое ожидание есть среднее значение случайной величины; математическое ожидание является наиболее простой характеристикой. Определение: пусть возможные значения случайной дискретной величины x1,…xn. И соответствующие им вероятности p1,…,pn. Если ряд сходится абсолютно, то его называют математическим ожиданием . Определение: если случайная величина непрерывна и имеет плотность Pξ(X), то математическое ожидание называется Mξ= , если только существует интеграл, который абсолютно сходится. Для произвольной случайной величины Mξ= .

Пример1. два игрока подбрасывают монету, если Г – первый игрок получает монету, Р – 1ый отдает монету. Mξ=(–1)*0.5+1*0.5=0.

Пример2. дискретное пространство W={1,2,…,k,…} P(k)=pk= положим 2 случайные величины ξ1=ξ1(k)=(–1)k ξ2=ξ2(k)=(–1)k Mξ1-? Mξ2-? 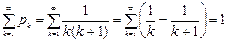=> ряд сходится. Проверим Мξ1 = -сходится абсолютно. -ряд Дирихле. Мξ2 = -расходится. 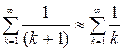-гармонический ряд. Мξ2 – существует, так как ряд абсолютных величин расходится Mξ1=

=

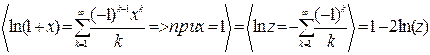
Мат ожидание наиболее распространенных распределений (смотри табличку – «легальную шпору») пример (как считать) Равномерное Mξ=

Свойства мат ожидания: (1) Mc=c c=const, так как Mc= (2) M(cξ)=cM(ξ) M(cξ)= (3) |Mξ| £ M|ξ| так как |Mξ|= (4) "ξ1,ξ2 M(ξ1+ξ2)=M(ξ1)+M(ξ2) (5) только для независимых ξ1,ξ2 M(ξ1*ξ2)=M(ξ1)*M(ξ2)

 

14.2. Дисперсия., средне квадратичное отклонение; свойства. Дисперсии наиболее распространенных распределений.

Моментные характеристики включают в себя: мат ожидание, дисперсию, средне квадратичное отклонение. Дисперсия – это мера рассеивания возможных значений случайной величины около ее мА ожидания. Dξ=M[ξ–Mξ]2 - среднеквадратическое отклонение Dξ=M[ξ–Mξ]2 = M[ξ2–2Mξ+(Mξ)2]=Mξ2 – M[2Mξ]+M[Mξ]= Mξ2 – 2MξMξ+Mξ Mξ= Mξ2 – MξMξ= Mξ2 – (Mξ)2 Mξ= Dξ=

свойства дисперсии: (1) Dξ ³0 так как дисперсия есть ожидание в квадрате, на квадрат любой величины (ξ–Mξ)2 ³0. (2) DC = 0 так как DC=M[C–MC] 2=M[C–C]=M(0) (3) D(Cξ) =C2Dξ так как DCξ=M[Cξ-M(Cξ)] 2 = M[C(ξ–Mξ)] 2 = C2M[ξ–M ξ]2 = C 2Dξ. (4) если ξ1, ξ2 независимы, то D(ξ1+ ξ2)=D(ξ1)+D(ξ2). {следствие: это свойство работает в случае конечного числа независимых переменных} Док-во (свойства 4) D(ξ1+ ξ2) = M[(ξ1+ ξ2)–M(ξ1+ ξ2)] 2=M[(ξ1–Mξ1)+ (ξ2–Mξ2)] 2=
=M[(ξ1–Mξ1) 2+2(ξ1–Mξ1)(ξ2–Mξ2)+ (ξ2–Mξ2) 2] = M[ξ1–Mξ1] 2 + 2M[(ξ1–Mξ1)(ξ2–Mξ2)] + M[ξ2–Mξ2] = < в среднем слагаемом виде мат ожидания 2-х величин, которые так же как и сами случайные величины не зависят между собой, а => это слагаемое можно представить>= D(ξ1)+2(Mξ1–Mξ1)(Mξ2–Mξ2)+D(ξ2) = D(ξ1)+D(ξ2) Дисперсию наиболее распространенных распределений переписать из таблички!

 

 

14.3. Моменты.

Определение: моментом k-того порядка случайной величины ξ называется мат ожидание k-ой степени [ξ–a]k nk(a)=M[ξ–a]k. если а=0, то имеем начальный момент k-того порядка: nk=Mξk Если a=Mξ, то имеем центральный момент k-того порядка mk=M[ξ–Mξ]k. m-абсолютный момент k-того порядка m=M|ξ –a|k. Mξ=n1 – начальный момент 1-го порядка. Dξ=m2 – центральный момент 2-го порядка. m1=0 – центральный момент первого порядка. Dξ=Mξ2 – (Mξ)2. m2=nk2 – (nk)2. Формулы связи центральных и начальных моментов mn=M(ξ–Mξ) n = =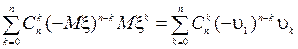
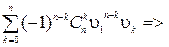
Формулы для расчета, подсчет момента ведется по формулам nk(a)= , где G-функция распределения (х–а) nk(a)= , F-функция распределения х. nk(а)= . Замечание: Мат ожидание существует тогда, когда изображающий его интеграл или сумма сходится абсолютно. Тогда момент k-того порядка величины ξ существует тогда и только тогда когда абсолютно сходится 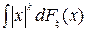. Теорема: если сл величина ξ имеет момент k-того порядка nk(а), то она имеет моменты всех положительных порядков меньших k. Док-во. Пусть r < k => |x|r<|x|k когда |x|>1.

= второй интеграл существует по предположению, а первый существует ввиду конечности пределов и ограниченности подинтегральной функции. Т.О. - существует.ЧТД.

 

14.4. Ковариация. Коэффициент корреляции.

Опр: ковариацией двух случайных величин называется число равное мат ожиданию произведения двух отклонений cov(ξ1,ξ2)= m11= mξ1ξ2 = M[(ξ1–Mξ1)(ξ2–Mξ2)]. Рабочий вариант формулы имеет вид: cov(ξ1,ξ2)= = M[(ξ1–Mξ1)(ξ2–Mξ2)] = M[ξ1ξ2 – (Mξ1)ξ2 – ξ1(Мξ2) + M(ξ1ξ2)]=M(ξ1ξ2)– Mξ1Mξ2 – Mξ1Mξ2 + Mξ1Mξ2 =
= M(ξ1ξ2) - Mξ1Mξ2. Если ξ1 = ξ2, то ковариация совпадает с дисперсией. cov(ξ1,ξ2)=M(ξ–Mξ)2=Dξ Свойства ковариации: (1) cov(Cξ1,ξ2)=C*cov(ξ1,ξ2), C=const (2) cov(ξ1,ξ2)=cov(ξ2, ξ1) D(ξ1+ξ2)=M[(ξ1+ξ2)–M(ξ1+ξ2)]2=M[(ξ1–Mξ1) 2 +2(ξ1–Mξ1)(ξ2–Mξ2)+(ξ2–Mξ2) 2]=M(ξ1–Mξ1)2+2M[(ξ1–Mξ1)(ξ2–Mξ2)]+M(ξ2–Mξ2)2= = Dξ1+Dξ2 +2cov(ξ1, ξ2). Отсюда видно, что в случае независимости величин ξ1, ξ2 cov(ξ1, ξ2)=0, если же cov(ξ1, ξ2)¹0 => ξ1, ξ2 – зависимы. Две случайные величины называются коррелированными, если их корреляционный момент (ковариация) отличен от нуля, и не коррелированны, если их ковариация =0.

Если ξ1, ξ2 коррелированны => ξ1, ξ2 – независимы. (обратное не всегда верно). ξ1, ξ2 – независимы => ξ1, ξ2 не коррелированны. Подсчет ковариации: m11=cov(ξ1, ξ2)= = (где 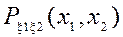- совместная плотность ξ1, ξ2) =

Определение: количественной характеристикой степени зависимости 2х случайных величин является коэффициент корреляции 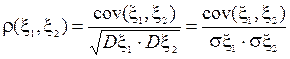Свойства коэффициента корреляции (1) | | £ 1, так как отношение двух величин находится |cov(ξ1, ξ2)| £ -1£cov(ξ1, ξ2)£1 (2) если ξ1, ξ2 независимы, то =0 так как cov(ξ1, ξ2)=0 (3) если одна из случайных величин является линейной функцией другой ξ2 =B+Aξ1, где А, В – const, то | |=1. Доказательство: Пусть Mξ1= a1, Dξ1=σ2 Mξ2 = M(B+Aξ1) = B+MAξ1=Aa+B Dξ1=D(B+Aξ1)=A2Dξ1 + DB=A2σ2. составим ковариацию: cov(ξ1, ξ2)=M[(ξ1–Mξ1)(B+Aξ1)–(Aa+B)]=AM[ξ1–Mξ1] 2=Aσ2. => | |=1 (замечание: равенство нулю коэффициента корреляции 2х случайных величин не является условием их независимости).

 

15.1. Закон больших чисел

В практической деятельности, а так же в общетеоретических задачах большое значение имеют события с вероятностями близкими к «1» или «0». Одной из основных задач в теории вероятности является установление закономерностей, происходящими с вероятностями близкими к «1», при этом основную роль должны играть закономерности, возникающие в результате наложения большого числа независимых или слабо зависимых случайных факторов. Закон больших чисел является одним из таких предложений, причем важнейшим. Определение: под законом больших чисел понимается вся совокупность предложений, утверждающих с вероятностью сколь угодно близкой к «1», что наступит некоторое событие, зависящее от неограниченно увеличивающегося числа случайных событий, любое из которых оказывает на него лишь незначительное влияние.

 

15.2. Некоторые оценки распределения случайных величин: нр-во Чебышева, теорема Чебышева.

Теорема: для любой случайной величины ξ, имеющей конечную дисперсию при любом положительном ε имеет место: вероятность того, что P{|ξ–Mξ| ³ ε}£ Dξ / ε2. Доказательство: Fξ(x) функция распределения. P{|ξ–Mξ| ³ ε}= (так как в области интегрирования можем задать оценку) £ =(мы только усилим неравенство, распространяя область интегрирования на все значения х)£ ЧТД. Замечание: другая форма неравенства Чебышева: вероятность того, что P{|ξ–Mξ| < ε} = 1– P{|ξ–Mξ| ³ ε}³ 1– Dξ / ε2. Теорема Чебышева: Если ξ1,… ξn,… последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченных одной и той же const (Dξ1 £С,…, Dξn £С,…) то, каково бы не было положительное ε>0 . Доказательство: В условиях теоремы дисперсия 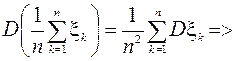(из попарной независимости следует независимость, поэтому дисперсия суммы = сумме дисперсий) => согласно неравенству Чебышева отсюда и следует требуемый предел Но вероятность не может быть > 1 поэтому остается ЧТД.

 

15.3. Частные случай теоремы Чебышева: теорема Бернулли; теорема Пуассона и др.

Теорема Бернулли: пусть m-число успехов в n-независимых испытаниях и p=P{“У”} – вероятность успеха в любом из испытании, тогда "ε>0 -частота успеха. Доказательство: Mξ=np, Dξ=npq. Пусть mk (k=1,2,…,n) – случайные величины равные числу успехов в каждом испытании. Тогда m = m1 +m2 +…+mn – общее число успехов в n-испытаниях. Мат ожидание любого mk равно Mmk = 1*p=p, Dmk =1*pq=pq £ ¼. По теореме Чебышева можем переписать . Теорема Пуассона: если в последовательности независимых испытаний вероятность успеха есть p(mk)=pk, то , где m = m1 +m2 +…+mn. Доказательство: по условию m = m1 +m2 +…+mn, Mmk = pk, Dmk = pkqk £ 1/4 – ограничены одной и той же const. Таким образом теорема Пуассона – частный случай теоремы Чебышева, в которой все Mmk заменяются pk. ЧТД. Теорема: если последовательность попарно независимых случайных величин ξ1,…, ξn,… такова, что Mξ1=…= Mξn=…= a, и Dξ1£C,…, Dξn£C,…, то для "ε>0 Этот частный случай теоремы Чебышева дает основание правилу среднего арифметического, постоянно употребляется в теории измерений.

15.4. Теорема Маркова.

Теорема: если последовательность случайных величин ξ1,… ξn,… такова, что при n→∞ выражение , то для "ε>0 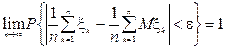. Если случайные величины ξk попарно независимы, то условие Маркова при n→∞ принимает вид , отсюда видно, что теорема Чебышева является частным случаем теоремы Маркова.

 

 

15.5. Усиленный закон больших чисел: неравенство Колмогорова, теорема Колмогорова.

Если взаимно независимые величины ξ1,… ξn имеют конечную дисперсию, то вероятность того, что , то есть вероятность совместного осуществления неравенств типа , когда к меняется от 1 до n, не меньше чем .

Будем говорить, что ξ1,… ξn – последовательность подчиняется закону больших чисел, если каковы бы ни были ε>0 и η>0 можно указать такое n0, что "s и для всех n: n0 £ n £ n0+s выполняется . Теорема Колмогорова Если последовательность взаимно независимых величин ξ1,… удовлетворяет условию 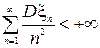, то она подчиняется усиленному закону больших чисел.

 

16.1. Производящие функции: свойства, теоремы, примеры.

Если ξ – целочисленная величина (целочисленные величины – это те, которые принимают целые неотрицательные значения) , то производящей функцией распределения называется функция (***), где хÎR или хÎС, |x| £1. Свойства jx(х): (1) производящая функция определена в любой точке отрезка [-1;1]. (2) jx(1)=1 (3) соотношение устанавливаемое формулой (***) между множеством производящих функций и множеством распределений является взаимнооднозначным: {jx(х)} <=> {Pk} Док-во(1): степенной ряд (***) мажорируется при |x|£1 рядом который для целочисленных значений равен 1, то есть сходящимся рядом при |x|£1 (если мажорируется, значит сходится). док-во(2): подставим вместо х=1, получим док-во(3) следствие при разложении в ряд Тейлора. Теорема: если случайные величины ξ1,… ξn независимы, то производящая функция jx1+…+ξn(х)= jx1(х)*jx2(х)*…* jxn(х) Доказательство: jx1+…+ξn(х)= Мхx1+…+ξn = М(x1*x2*…* xn)= Мx1*Мx2*…* Мxn = =jx1(х)*jx2(х)*…* jxn(х).

 

Пример: пусть ξ – случайная величина, имеющая биномиальный закон распределения. .

Пример найдем функцию биномиального распределения с помощью последней теоремы: m = ξ1 +ξ2 +…+ξn, где Р{ξk=1}=1–P{ξk=0} k=0,1,…,n jm(х)= jx1+…+ξn(х)= jx1(х)*jx2х)*…* jξn(х) =

 

16.2. Характеристические функции, свойства, теоремы.

Определение: характеристической функцией случайной величины ξ называется fξ(t)=Meitξ tÎ(-∞;+∞), eitξ – комплекснозначная случаная величина. В общем виде комплексная случайная величина определяется ξ1(w) + iξ2(w), wÎW (ξ1, ξ2)- случайный вектор. Мат ожидание M(ξ1+iξ2) = Mξ1+iMξ2. eitξ = cos tξ + i*sin tξ => Meitξ = M(cos tξ) + iM(sin tξ) => fξ(t)=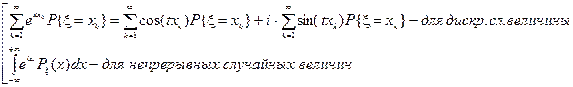

Замечание: плотность распределения однозначно выражается через характеристическую функцию 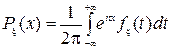свойства характеристической функции: (1) характеристическая функция определена для любого t меняющегося (-∞; +∞) (2) fx(0)=1, a |fx(t)|£1 (3) если случайная величина η= – линейная функция ξ, а и b – const, то f η(t) = eitb*fx(at) (4) соотношение, устанавливаемое формулой fξ(t)=Meitξ между множеством характеристических функций и множеством функций распределений взаимнооднозначно {fx(t)} <=> {Fx(t)}. Док-во (1,2) "tÎR -∞<t<+∞ fξ(0)=Mei0ξ = M*1=1=const. (3) по определению fξ(у)=Meitη = Meit (аξ+b) = ei t b *Мe i tаξ = eitbfx(at) (4) является свойством разложения функции в ряд Тейлора. ЧТД. Теорема: если существует абсолютный к-тый момент случайной величины ξ: М|ξ|k<∞, k³1, то существует к-тая производная fξ(k)(t), причем в точке 0. fξ(k)(0)= ik*Mξk.пусть ξ – абсолютно непрерывная величина, то есть интеграл сходится равномерно по t, что дает возможность дифференцировать под интегралом: fξ'(t)= . Предположи не существует производной степени l, l<k => таким образом Эта теорема позволяет весьма просто вычислять моменты величин, если известна ее характеристическая функция. ЧТД. Теорема: Если случайные величины ξ1,…, ξn – независимы fξ1…ξn (t)= fξ1(t)*…*fξn(t). докажем для n=2. fξ1ξ2 (t)=Меit(ξ1+ξ2) = Меitξ1 * Меitξ2 = M[(cos tξ1 + i sintξ1)(cos tξ2 + i sintξ2)]= M(cos tξ1 *cos tξ2) +
+ M(i sintξ1*cos tξ2) + M(i cos tξ1*sin tξ2) – M(sintξ2*sin tξ1) =(разобьем мат ожидания)= Mcos tξ1*Мcos tξ2+ + iMsintξ1*Mcos tξ2 + iMcos tξ1*Msin tξ2 – Msintξ2*Msin tξ1 = (Mcos tξ1 + iMsintξ1)(Mcos tξ2 + iMsintξ2) = M(cos tξ1 + i sintξ1)*M(cos tξ2 + i sintξ2) = Meitξ1*Mei tξ2 = fξ1(t)*fξ2(t) чтд. (Дальше по индукции) ЧТД.

 

 

16.3. Примеры подсчета характеристических функций.

ПРИМЕР1: В партии состоящей из n деталей, m – дефектных. Для проверки качества произведена выборка, состоящая из r изделий m<r<(n–m) n=m+(n–m) Найти характеристическую функцию числа дефектных изделий содержащихся в выборке. Решение: ξ-число дефектных изделий в выборке (может принимать только целое значение в интервале от 0 до m) Пусть mk = P{ξ =k} k=0,1,2,…,m => характеристическая функция

ПРИМЕР2: найти характеристическую функцию случайной величины, плотность которой Pξ(x) = 0.5e–|x|. Решение: так как ξ – непрерывная функция, то =>
ПРИМЕР3: случайная величина ξ имеет характеристическую функцию найти Рξ(х)-?

Решение: плотность вероятности связана с характеристической функцией следующей формулой будем рассматривать t как вещественную часть комплексного переменного w=t+ir => t =Rew При х-отрицательном интеграл по вещественной оси равен интегралу по замкнутому контуру, состоящему из вещественной оси и полуокружности бесконечно большого радиуса, лежащего в верхней полуплоскости (как на рисунке) . При х>0 поступаем следующим образом Таким образом получаем ПРИМЕР4: найти характеристическую функцию случайной величины ξ, распределенной по закону Пуассона. Решение: k=0,1,2,… 0<λ<∞ fξ(t)=Meitξ = ПРИМЕР5: найти характеристическую функцию равномерного распределения величины в интервале (-а; а). Решение:

16.4. Предельные теоремы для характеристических функций (прямая и обратная)

Определение: условимся говорить, что последовательность неубывающих функций F1(x),F2(x),…,Fn(x),… сходится в основном к функции распределения неубывающей функции F(x), если при n→∞ она сходится к F(x) для любой ее точки непрерывности, то Fn(-∞)=0.

Теорема(прямая): если последовательность функций распределения сходится в основном к (F1(x),F2(x),… → F(x)), то последовательность характеристических функций сходится к характеристической функции f(t) (f1(t),f2(t),…,fn(t),… → f(t)). Эта сходимость равномерна в любом конечном интервале t.

Обратная предельная теорема: Если последовательность характеристических функций f1(t),f2(t),…,fn(t),… → f(t), то последовательность функций распределения сходится в основном к некоторой функции F(x) (F1(x),F2(x),… → F(x))

 

16.5. Формула обращения для характеристической функции.

По функции распределения fξ может определить характеристическую функцию. Предложение: по характеристической функции функция распределения определяется однозначно. Теорема1: Пусть fξ(t), Fξ(x) – характеристическая функция и функция распределения случайной величины ξ. Если x1,x2 точки непрерывности функции распределения Fξ(x) то приращение этой функции (***) Fξ(x2)–Fξ(x1)= Док-во: рассмотрим отдельно интеграл 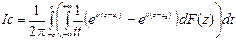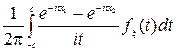=(из определения характеристической функции)=(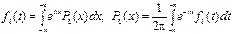)= (изменим порядок интегрирования, так как по z интеграл абсолютно сходится, а по t пределы интеграла конечны) =

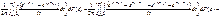
= =(причем эта сходимость равномерна относительотносительно a в любой области a>δ>0 или 0<a<–δ и при |a|<δ и при всех с)=