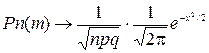Формула полной вероятности. Примеры.
Пусть произвольное событие А может осуществиться с одним и только одним из n-попарно-несовместных событий В1,…,Вn, BiÇBj=Æ, образующих полную группу событий, тогда  вероятность нескольких событий А
вероятность нескольких событий А  Bi – называют гипотезами. Пример. Две урны (2б +4ч) и (3б+2ч) вынимают по 1 шару. Из этих двух вынимают один. Какова вероятность, что он белый. А={извлечь из пары шаров белый}В1={2б шара в паре}В2={2ч шара в паре}В3={1ч+1б в паре}. Р(А)=
Bi – называют гипотезами. Пример. Две урны (2б +4ч) и (3б+2ч) вынимают по 1 шару. Из этих двух вынимают один. Какова вероятность, что он белый. А={извлечь из пары шаров белый}В1={2б шара в паре}В2={2ч шара в паре}В3={1ч+1б в паре}. Р(А)=  =Р(В1)Р(А/В1)+Р(В2)Р(А/В2)+Р(В3)Р(А/В3) Р(В1)=2/6*3/5=1/5 Р(В2)=4/6*2/5=4/15 Р(В3)=2/6*2/5+4/6*3/5=8/15 Р(В1)+Р(В2)+Р(В3)=1 – необходимое условие. Р(А/В1) = 1, Р(А/В2) = 0, Р(А/В3) = 1/2, Р(А)=1/5+4/15=7/15
=Р(В1)Р(А/В1)+Р(В2)Р(А/В2)+Р(В3)Р(А/В3) Р(В1)=2/6*3/5=1/5 Р(В2)=4/6*2/5=4/15 Р(В3)=2/6*2/5+4/6*3/5=8/15 Р(В1)+Р(В2)+Р(В3)=1 – необходимое условие. Р(А/В1) = 1, Р(А/В2) = 0, Р(А/В3) = 1/2, Р(А)=1/5+4/15=7/15
Формула Байеса (вероятности гипотез). Примеры.
Пусть в условии задачи: даны две урны (2б +4ч) и (3б+2ч) вынимают по 1 шару. Из этих двух вынимают один. Какова вероятность, что он белый. А={извлечь из пары шаров белый}В1={2б шара в паре}В2={2ч шара в паре}В3={1ч+1б в паре} Р(А)=  . Событие А произошло. Воспользуемся теоремой умножения вероятности Р(ВiA)=P(A)P(Bi/A)=P(Bi)P(A/Bi) откуда =>Р(Bi/A)=P(Bi)P(A/Bi) / P(A) = P(Bi)P(A/Bi) /
. Событие А произошло. Воспользуемся теоремой умножения вероятности Р(ВiA)=P(A)P(Bi/A)=P(Bi)P(A/Bi) откуда =>Р(Bi/A)=P(Bi)P(A/Bi) / P(A) = P(Bi)P(A/Bi) /  - формула Байеса. Пример. В трех урнах (2б+3ч) (3б+2ч) (4б+1ч). Наудачу выбран белый шар. Какова вероятность, что шар из третьей урны. А={белый шар из наудачу выбранной урны}. Вi ={белый из i-той урны} i=1,2,3. Р(B3/A) -?
- формула Байеса. Пример. В трех урнах (2б+3ч) (3б+2ч) (4б+1ч). Наудачу выбран белый шар. Какова вероятность, что шар из третьей урны. А={белый шар из наудачу выбранной урны}. Вi ={белый из i-той урны} i=1,2,3. Р(B3/A) -?  Брошено две игральные кости. Какова вероятность того, что выпало «33», если известно, что сумма выпавших очков делится на 3. А={21,12,15,51,24,42,66,33,36,63,54,45} |A|=12 B={33}=P(AB) |B|=1; P(A/B)=P(AB)/P(A)=1/12
Брошено две игральные кости. Какова вероятность того, что выпало «33», если известно, что сумма выпавших очков делится на 3. А={21,12,15,51,24,42,66,33,36,63,54,45} |A|=12 B={33}=P(AB) |B|=1; P(A/B)=P(AB)/P(A)=1/12
9. Повторение испытаний. Схема Бернулли. Примеры.
В научной и практической деятельности постоянно приходится проводить многократно повторяющиеся испытания в сходных условиях. При этом как правило результаты предшествующих испытаний никак не сказываются на последующие. Простейший тип таких испытаний – это когда некоторое событие А появляется в каждом испытании с одной и той же ненулевой вероятностью Р. Причем Р не зависит от результатов предшествующих и последующих результатов. Объясненная ситуация называется схемой Бернулли. Под элементарными событиями в схеме Бернулли понимается последовательность наступлений или ненаступления события А (наступил – успех «У», ненаст – неудача «Н»). Пример. Подбрасывание монеты n=3 {ННН, HHY,HYH,YHH,YYH,HYY,YHY,YYY} 2n=8 Вероятностная мера на множестве элементарных событий вводится однозначно Р(А)=У=р Р( )=Н=1–р=q. Число исходов в схеме Бернулли – два (У или Н) – Биномиальная схема распределения вероятности. В схеме Бернулли У и Н независимы и в силу теоремы (умножения вероятности независимых событий) вероятность того, что в n испытания событие А появится ровно m раз равно pmqn-m. Вопрос только в том, что на каких местах этой цепочке У и Н:
)=Н=1–р=q. Число исходов в схеме Бернулли – два (У или Н) – Биномиальная схема распределения вероятности. В схеме Бернулли У и Н независимы и в силу теоремы (умножения вероятности независимых событий) вероятность того, что в n испытания событие А появится ровно m раз равно pmqn-m. Вопрос только в том, что на каких местах этой цепочке У и Н:  Вероятность того, что успех появится m раз в n испытаниях считается по формуле
Вероятность того, что успех появится m раз в n испытаниях считается по формуле  - формула Бернулли.
- формула Бернулли.  . Так как вероятность в формуле Бернулли является коэффициент при xm разложения бинома (p+qx)n, то совокупность вероятностей называют биномиальным законом распределения вероятности
. Так как вероятность в формуле Бернулли является коэффициент при xm разложения бинома (p+qx)n, то совокупность вероятностей называют биномиальным законом распределения вероятности  Так как при х=1 это можно представить
Так как при х=1 это можно представить  . ПРИМЕР Проведено 10 НЗ испытаний, любой из которых заключался в одновременном подбрасывании 3х игральных костей. Найти вероятность того, что в 4х испытаниях появится точно две шестерки. N=10 m=4 p=P(A)=P(“Y”) “Y” – при подбрасывании трех костей. 1–p=q = P(“H”) p=P(A)=P(“Y”)=()1/6*1/6*5/6)*3=5/72 q=67/72 P10(4)=
. ПРИМЕР Проведено 10 НЗ испытаний, любой из которых заключался в одновременном подбрасывании 3х игральных костей. Найти вероятность того, что в 4х испытаниях появится точно две шестерки. N=10 m=4 p=P(A)=P(“Y”) “Y” – при подбрасывании трех костей. 1–p=q = P(“H”) p=P(A)=P(“Y”)=()1/6*1/6*5/6)*3=5/72 q=67/72 P10(4)=  =3,2*10-3 Если нужно найти наивероятнейшее число успехов в n испытаниях np–q£k0£np+q p=P(“Y”) q=P(“H”) подбрасываем монету три раза n=3
=3,2*10-3 Если нужно найти наивероятнейшее число успехов в n испытаниях np–q£k0£np+q p=P(“Y”) q=P(“H”) подбрасываем монету три раза n=3 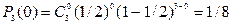


 k0=1 k0=2 Если np – сразу целое, то k0=np Если np–q – целое, то k0 и k0+1 – два числа. Если np-q – дробное, то k0 первое целое число, превосходящее дробь np–q.
k0=1 k0=2 Если np – сразу целое, то k0=np Если np–q – целое, то k0 и k0+1 – два числа. Если np-q – дробное, то k0 первое целое число, превосходящее дробь np–q.
3*1/2–1/2£ k0 £ 3*1/2+1/2 => 1£k0£2 np-q+1 = np+(1-q)=np+p. если в схеме Бернулли n→∞, то вычисление очень сложно. Поэтому в таких случаях, когда n→∞ а p→0 пользуемся. np=λ
Pm(λ)= 
10.1. Теорема Пуассона:
Формула Пуассона когда n→∞ а p→0 np=λ 0£λ£∞ вероятность появления в n испытания успеха ровно m раз равна  → Pm(λ)=
→ Pm(λ)=  - формула Пуассона. Док-во:
- формула Пуассона. Док-во:  =
= 
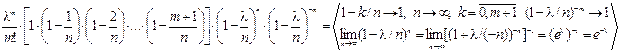 = λme–λ/m! ЧТД!!! Замечание: если малы q, то пуассоновским приближением можно воспользоваться для числа неудач. Задача: учебник издан тиражом n=100000 экземпляров: p=0.0001 неправильная брошюровка. Найти Р того, что тираж содержит ровно 5 бракованных книг.
= λme–λ/m! ЧТД!!! Замечание: если малы q, то пуассоновским приближением можно воспользоваться для числа неудач. Задача: учебник издан тиражом n=100000 экземпляров: p=0.0001 неправильная брошюровка. Найти Р того, что тираж содержит ровно 5 бракованных книг.
m=5 λ=np=10 P100000(5) = P5(10)=105e-10 / 5! = 0.0375.
10.2. Локальная теорема Муавра-Лапласа:
Есои вероятность наступления некоторого события в n испытаниях постоянна и 0<p<1 то вероятность того, что в этих испытаниях успех появится ровно m раз удовлетворяет при n→∞ соотношению  равномерно для всех х для которых x=xnm=
равномерно для всех х для которых x=xnm=  . Практически вычисляется это следующим образом
. Практически вычисляется это следующим образом  функция j табулирована, то есть ее значения представлены в таблице в задачниках по теории вероятности. Для того, чтобы использовать ее значения нужно знать следующие свойства. СВОЙСТВА: 1) j(–х)= j(х) 2) х³4 => j(x)→0. Доказательство. Для док-ва нам понадобится формула Стирлинга
функция j табулирована, то есть ее значения представлены в таблице в задачниках по теории вероятности. Для того, чтобы использовать ее значения нужно знать следующие свойства. СВОЙСТВА: 1) j(–х)= j(х) 2) х³4 => j(x)→0. Доказательство. Для док-ва нам понадобится формула Стирлинга  при больших s. остаточный показатель |qs|£1/12s
при больших s. остаточный показатель |qs|£1/12s 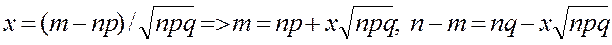 Из этих представлений видно, что если х остается в каком-либо ограниченном отрезке, то числа m и m-n возрастают до ∞ вместе с n→∞, это позволяет применить формулу Стирлинга. Возьмем формулу Бернулли
Из этих представлений видно, что если х остается в каком-либо ограниченном отрезке, то числа m и m-n возрастают до ∞ вместе с n→∞, это позволяет применить формулу Стирлинга. Возьмем формулу Бернулли  =
=
 ;
;
где остаточный показатель q=qn - qn–m<1/12*[1/n+1/m+1/(n+m)]. Из оценки q => каков бы ни был отрезок изменения х (а£х£b) величина q равномерно относительно х в этом отрезке стремится к нулю при n→∞ => eq→1. Пусть  прологарифмируем
прологарифмируем 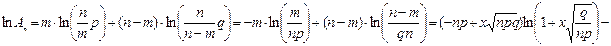
 в условиях теоремы при достаточно больших n элементы
в условиях теоремы при достаточно больших n элементы  Это позволяет разложить ln в степенной ряд. Ограничимся 1м и 2м членами разложения. ln(1+x)=x-x2/2+0(x3). Тогда
Это позволяет разложить ln в степенной ряд. Ограничимся 1м и 2м членами разложения. ln(1+x)=x-x2/2+0(x3). Тогда 
 =
=  . Равномерно в любом конечном отрезке х. Т.О.
. Равномерно в любом конечном отрезке х. Т.О.  →
→  . Оценим теперь
. Оценим теперь  . Рассмотрим выражение
. Рассмотрим выражение  =>
=> 
 . Тогда получаем
. Тогда получаем