дискретной случайной величины

Закон распределения. Ряд распределения

Законом распределения случайной величины называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной.

Рядом распределения дискретной случайной величины Х называется таблица, в верхней строке которой перечислены в порядке возрастания все возможные значения случайной величины а в нижней – вероятности этих значений: При этом – вероятность того, что в результате опыта случайная величина Х примет значение .

Ряд распределения записывается в виде таблицы

Х:			…		…
		…		…	.

 

 

(4.1)

 

События ; ; … несовместны и образуют полную группу, поэтому сумма всех вероятностей в (4.1) будет равна единице: . (4.2)

Отсюда следует, что единица распределена между возможными значениями случайной величины.

Пример. Ряд распределения случайной величины Х

Х:
0,24	0,46	0,26	0,04	.

 

(4.3)

 

Графическое изображение ряда распределения называется многоугольником распределения.

Строится он так: для каждого возможного значения случайной величины восстанавливается перпендикуляр к оси абсцисс, на котором откладывается вероятность данного значения случайной величины. Полученные точки для наглядности соединяются отрезками прямых (см. рис. 4.1).

Кроме этой геометрической интерпретации, часто полезна механическая интерпретация, при которой ряд распределения рассматривается как ряд материальных точек на оси абсцисс, имеющих значения , и соответственно массы в сумме составляющие единицу (см. рис. 4.2).

 

Функция распределения

Наиболее общей формой закона распределения, пригодной как для дискретных, так и недискретных случайных величин, является функция распределения.

Функцией распределения случайной величины Х называется вероятность того, что она примет значение меньшее, чем заданное х (аргумент функции) 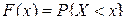. (4.4)

Геометрически определение (4.4) интерпретируется как вероятность того, что случайная точка попадает левее заданной точки (см. рис. 4.3).

Свойства функции распределения выводятся из геометрической интерпретации (см. рис. 4.3–4.4):

1. – неубывающая функция своего аргумента, т. е. если , то .

Для доказательства представим событие как сумму двух несовместных событий (см. рис. 4.4)

, где

.

По правилу сложения вероятностей

; .

Учитывая выражение (4.4), получаем , (4.5)

но так как , то окончательно имеем, что

.

2. ; .

Перемещая до бесконечности влево (при ) или вправо (при ), можно убедиться, что событие становится либо невозможным , либо достоверным .

Функция распределения любой случайной величины есть неубывающая функция своего аргумента, значения которой заключены между нулем и единицей; причем , а . В отдельных точках эта функция может иметь скачки (разрывы первого рода), на некоторых участках она может быть постоянной, на других – монотонно возрастать (см. рис. 4.5).

С помощью функции распределения можно вычислить вероятность попадания случайной точки на участок от до . Для определенности левый конец участка будем включать в него, а правый – нет.

Искомую вероятность получаем из выражения (4.5), положив и ,

,

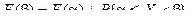Откуда . (4.6)

Таким образом, вероятность того, что случайная величина Х в результате опыта попадет на участок от до 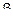(включая ), равна приращению функции распределения на этом участке (см. рис. 4.6). Другая запись выражения (4.6) ,

где квадратная скобка означает, что данный конец включается в участок, а круглая – что не включается.

Вероятность отдельного значения случайной величины. Если взять любую точку и примыкающий к ней участок , то, приближая 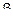к , в пределе получаем . (4.7)

Значение этого предела зависит от того, непрерывна ли функция в точке или терпит разрыв. Если функция в точке совершает скачок, то предел (4.7) равен величине этого скачка. Если же везде непрерывна, то вероятность каждого отдельного значения случайной величины Х равна нулю. Последнее утверждение не означает, что событие невозможно; оно возможно, но с нулевой вероятностью.

Функция распределения дискретной

случайной величины

Для случайной величины Х, представленной рядом распределения

Х:
0,24	0,46	0,26	0,04	,

 

можно, задаваясь различными значениями х, вычислить функцию распределения :

;

;

;

;

.

На рис. 4.7 приведена рассчитанная функция распределения . Жирными точками отмечены значения в точках разрыва; функция при подходе к точке разрыва слева сохраняет свое значение (функция "непрерывна слева"). Заметим, что между скачками функция постоянна.

Функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений. Сумма всех скачков функции распределения равна единице.

Индикатор события. Индикатором события А называется случайная величина , равная единице, если в результате опыта событие А произошло, и – нулю, если не произошло:

Ряд распределения случайной величины с вероятностью события А, равной , имеет вид

:
		.

 

 

Многоугольник распределения случайной величины приведен на рис. 4.9, а функция распределения – на рис. 4.10.

 

 

Непрерывная случайная величина.

Плотность распределения

Случайная величина Х называется непрерывной, если функция распределения не только непрерывна в любой точке, но и дифференцируема всюду, кроме, может быть, отдельных точек, где она терпит излом (см. рис. 4.11). Так как скачков эта функция не имеет, то вероятность любого отдельного значения непрерывной случайной величины равна нулю, т. е.

.

Поэтому говорить о распределении вероятностей отдельных значений не имеет смысла. В качестве закона распределения непрерывных случайных величин вводится понятие плотности распределения вероятностей или плотности распределения.

Исходим из механической интерпретации распределения вероятностей. Для дискретной случайной величины Х в точках сосредоточены массы , сумма которых равна единице. Для непрерывной случайной величины масса, равная 1, "размазана" по числовой оси с непрерывной в общем случае плотностью (см. рис. 4.12). Вероятность попадания случайной величины Х на любой участок может быть интерпретирована как масса, приходящаяся на этот участок, а средняя плотность на этом участке – как отношение массы к его длине. Для участка .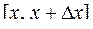

Но вероятность определяется как приращение функции распределения на этом участке ,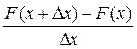

и, переходя к пределу при , получаем плотность в точке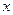

, т. е. производную функции распределения.

Плотностью распределения непрерывной случайной величины Х в точке х называется производная ее функции распределения в этой точке . (4.8)

Плотность распределения , как и функция распределения , является одной из форм закона распределения, но она существует только для непрерывных случайных величин. График плотности распределения называется кривой распределения (см. рис. 4.13).

Вероятность попадания случайной величины Х на участок с точностью до бесконечно малых высших порядков равна . Эта величина называется элементом вероятности и геометрически равна (приближенно) площади элементарного прямоугольника, опирающегося на отрезок длиной и примыкающего к точке (см. рис. 4.13).

Вероятность попадания случайной величины Х на участок от до равна сумме элементов вероятности на всем этом участке, т. е. интегралу вида

. (4.9)

В геометрической интерпретации эта вероятность равна площади фигуры, ограниченной сверху кривой распределения и опирающейся на участок 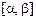(см. рис. 4.14). Функция распределения теперь может быть вычислена следующим образом: 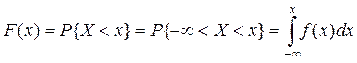. (4.10)

 

Геометрически (см. рис. 4.14) – это площадь, ограниченная сверху кривой распределения и лежащая левее точки .

Свойства плотности распределения.

1. Плотность распределения – неотрицательная функция

,

как производная от неубывающей функции, и еще потому, что плотность, как физическая величина, не может быть отрицательной.

2. Интеграл в бесконечных пределах от плотности вероятности равен единице, т. е. (4.11)

Это свойство вытекает из выражения (4.10), если верхний предел будет и если учесть, что .

 

Числовые характеристики положения

Закон распределения полностью описывает случайную величину с вероятностной точки зрения. Но часто достаточно указать только отдельные числовые параметры, которые позволяют в сжатой форме выразить наиболее существенные черты распределения. Такие параметры называются числовыми характеристиками случайной величины.

Среди числовых характеристик можно выделить характеристики положения, т. е. некие средние, ориентировочные значения случайной величины, около которых группируются ее возможные значения.

Математическое ожидание. Из характеристик положения наибольшую роль играет математическое ожидание, которое иногда называют просто средним значением.

Определим математическое ожидание исходя из механической интерпретации распределения случайной величины. Если считать, что единичная масса распределена между точками на оси абсцисс со значениями (см. рис. 4.2), то центр масс такой системы материальных точек будет иметь координату :

, но ,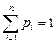

тогда

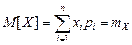. (4.12)

Это среднее взвешенное значение случайной величины , в которое координата каждой точки 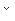входит с "весом", равным соответствующей вероятности, и называется математическим ожиданием.

Математическим ожиданием дискретной случайной величины называется сумма произведений всевозможных ее значений на вероятности этих значений.

В том случае, когда ,

.

Но бесконечная сумма может и расходиться, т. е. соответствующая случайная величина не будет иметь математического ожидания.

Пример. Случайная величина , заданная рядом распределения

Х:					…		…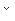
				…		…	,

 

 

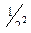
имеет расходящееся математическое ожидание, так как

,

и, значит, у такой случайной величины математического ожидания не существует.

При переходе к непрерывной случайной величине необходимо в формуле (4.12) заменить суммирование интегрированием, а вероятность – элементом вероятности:

. (4.13)

Область интегрирования определяется областью существования функции .

Для смешанной случайной величины можно записать, что

,

где сумма распространяется на все значения 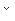, имеющие отличные от нуля вероятности, а интеграл на все участки, где функция распределения непрерывна; множество участков непрерывности обозначено через .

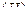Пользуясь интегралом Стилтьеса, можно записать выражение для математического ожидания любой случайной величины через ее функцию распределения в виде

.

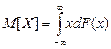Мода. Следующая характеристика положения – это мода. Модой случайной величины называют ее наиболее вероятное значение, т. е. то, для которого вероятность или плотность распределения достигают максимума. Моду обычно обозначают через . Если многоугольник вероятности или плотность распределения достигают максимума в нескольких точках, то такие распределения называют полимодальными (см. рис. 4.16).

Медиана. Еще одна характеристика положения непрерывных случайных величин. Медианой непрерывной случайной величины называется такое ее значение , для которого

,

т. е. одинаково вероятно, окажется ли случайная величина меньше или больше .

Геометрически медиана – это координата той точки на оси , для которой площади, лежащие слева и справа от нее, одинаковы и равны по (см. рис. 4.17). Для симметричных распределений математическое ожидание, мода и медиана совпадают.

 

 

Моменты. Дисперсия и среднее квадратичное

отклонение

Другие числовые параметры случайных величин характеризуют различные особенности распределения. Особое значение имеют начальные и центральные моменты.

Начальным моментом -го порядка случайной величины называется математическое ожидание -й степени этой величины:

.

Для дискретной случайной величины начальный момент -го порядка определяется суммой ,

где 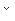– возможные значения случайной величины , – соответствующие вероятности.

Для непрерывной случайной величины по аналогии имеем , где – плотность распределения.

Необходимо отметить, что ранее введенная характеристика положения – математическое ожидание случайной величины – есть не что иное, как первый начальный момент, т. е. .

Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания

.

Очевидно, что математическое ожидание центрированной случайной величины равно нулю:

.

Аналогично и для непрерывной случайной величины.

Центрирование случайной величины равносильно переносу начала отсчета в точку . Моменты центрированной случайной величины называются центральными моментами. Они аналогичны моментам относительно центра масс в механике.

Центральным моментом -го порядка случайной величины называют математическое ожидание -й степени центрированной случайной величины:

.

При этом для дискретной случайной величины получаем ,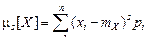

а для непрерывной .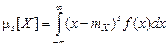

Для любой случайной величины центральный момент 1-го порядка равен нулю: .

Центральные и начальные моменты связаны между собой. Так, для моментов второго порядка

.

Аналогично для третьего порядка .

Особое значение имеет второй центральный момент , который называется дисперсией случайной величины:

; .

Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной величины. Для вычисления дисперсии служат формулы: ; ; .

Дисперсия случайной величины равна математическому ожиданию ее квадрата минус квадрат математического ожидания.

Дисперсия случайной величины характеризует рассеяние, разбросанность случайной величины около ее математического ожидания. Само слово дисперсия означает "рассеяние".

Дисперсия имеет размерность квадрата случайной величины, и поэтому часто используется среднее квадратичное отклонение .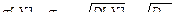

Для неотрицательной случайной величины в качестве характеристики "степени ее случайности" иногда применяют коэффициент вариации .

Таким образом, основные числовые характеристики случайной величины – математическое ожидание, дисперсия и среднее квадратичное отклонение. Они характеризуют как положение случайной величины, так и степень ее разбросанности. Для них очевидны следующие свойства:

1. Математическое ожидание неслучайной величины С равно самой неслучайной величине С: .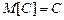

2. Дисперсия неслучайной величины С равна нулю, так как у такой величины нулевое рассеивание .

3. При прибавлении к случайной величине Х неслучайной величины С к ее математическому ожиданию прибавляется та же величина: .

4. При прибавлении к случайной величине Х неслучайной величины С ее дисперсия не изменяется: .

5. При умножении случайной величины Х на неслучайную величину С на ту же величину умножается ее математическое ожидание: .

6. При умножении случайной величины Х на неслучайную величину С ее дисперсия умножается на : .

7. При умножении случайной величины Х на неслучайную величину С ее среднее квадратичное отклонение умножается на модуль : .

Третий центральный момент служит для характеристики асимметрии ("скошенности") распределения. Для симметричных относительно математического ожидания распределений все нечетные центральные моменты равны нулю: ,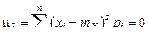

так как каждому положительному слагаемому соответствует равное по модулю отрицательное.

Третий центральный момент имеет размерность куба случайной величины, и для получения безразмерной характеристики – коэффициента асимметрии – делят на : , show – "косой".

На рис. 4.17 приведены две плотности распределения: у положительный коэффициент асимметрии, а у – отрицательный.

Четвертый центральный момент характеризует островершинность ("крутость") распределения. Это свойство определяется с помощью так называемого эксцесса

.

За норму выбирается нормальное распределение, у которого отношение и соответственно эксцесс равен нулю. Поэтому распределения более островерхие, чем нормальное, имеют положительный эксцесс, а менее островерхие (плосковерхие) – отрицательный (см. рис. 4.18).

 

 

Производящая функция

Пусть имеется случайная величина , принимающая неотрицательные целочисленные значения с вероятностями , где .

Производящей функцией для случайной величины называется функция вида

, (4.14)

где – аргумент функции .

Коэффициенты при равны вероятностям того, что случайная величина примет значение . В случае, когда число возможных значений конечно , выражение (4.14) сохраняет силу, так как при все вероятности обращаются в нуль. При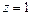

.

Если взять первую производную по от производящей функции, то .

При получаем .

Но это математическое ожидание случайной величины , т. е. математическое ожидание неотрицательной целочисленной случайной величины равно первой производной ее производящей функции при .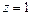

Возьмем вторую производную производящей функции .

При 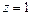имеем .

Первая сумма – это второй начальный момент случайной величины , а вторая – ее математическое ожидание, откуда получаем ,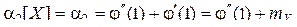

т. е. второй начальный момент случайной величины равен сумме второй и первой производных производящей функции при .

Аналогично, взяв третью производную, получаем при .

Таким образом, в случае необходимости можно выразить начальные моменты более высокого порядка через моменты более низкого.

 

Биноминальное распределение

Дискретная случайная величина имеет биноминальное распределение, если ее возможные значения имеют соответствующие вероятности:

, (4.15)

где .

Биноминальное распределение (4.15) зависит от двух параметров, 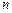и . Это распределение случайной величины – числа появления события в 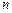независимых испытаниях, в каждом из которых событие может наступить с вероятностью .

Для определения числовых характеристик случайной величины ,распределенной по биноминальному закону, найдем ее производящую функцию

. (4.16)

Для нахождения математического ожидания продифференцируем (4.16)

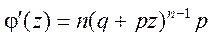
и при 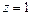получаем .

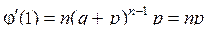Таким образом, математическое ожидание случайной величины , распределенной по биноминальному закону, будет равно .

Аналогично вычисляем вторую производную: ,

при имеем .

Второй начальный момент

,

а дисперсия случайной величины , распределенной по биноминальному закону, будет иметь вид

.

Таким образом, получили ; ; . (4.17)

 

Распределение Пуассона

Дискретная случайная величина имеет распределение Пуассона, если ее возможные значения (бесконечное, но счетное множество) имеют соответствующие вероятности:

. (4.18)

Распределение Пуассона зависит лишь от одного параметра , который является одновременно и математическим ожиданием, и дисперсией случайной величины . Для доказательства этого утверждения запишем производящую функцию в виде 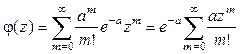. Учитывая, что 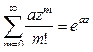, получаем . (4.19)

Первая производная производящей функции при 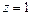равна математическому ожиданию случайной величины : .

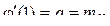Вторая производная при 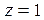будет равна , а второй начальный момент . И наконец, дисперсия случайной величины .

Пуассоновское распределение является предельным случаем биноминального, когда число независимых опытов неограниченно возрастает и одновременно вероятность (успех в каждом опыте) неограниченно уменьшается, при этом произведение в пределе становится равным :

Из предельного свойства следует, что распределение Пуассона с параметром можно применять вместо биноминального, когда число опытов 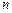очень велико, а вероятность очень мала, т. е. в каждом отдельном опыте событие наступает крайне редко. Поэтому распределение Пуассона часто называют "законом редких событий".

&n